Difference between revisions of "2002 AMC 12B Problems/Problem 14"
(soln) |
5849206328x (talk | contribs) m |
||
| Line 9: | Line 9: | ||
== Solution == | == Solution == | ||
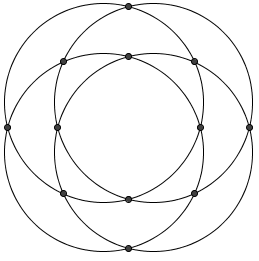
| − | For any given pair of circles, they can intersect at most <math>2</math> times. Since there are <math>{4\choose 2} = 6</math> circles, the maximum number of possible intersections is <math>6 \cdot 2 = 12</math>. We can construct such a situation as below, so the answer is <math>\mathrm{(D)}</math>. | + | For any given pair of circles, they can intersect at most <math>2</math> times. Since there are <math>{4\choose 2} = 6</math> pairs of circles, the maximum number of possible intersections is <math>6 \cdot 2 = 12</math>. We can construct such a situation as below, so the answer is <math>\mathrm{(D)}</math>. |
[[Image:2002_12B_AMC-14.png]] | [[Image:2002_12B_AMC-14.png]] | ||
Revision as of 21:01, 21 June 2009
Problem
Four distinct circles are drawn in a plane. What is the maximum number of points where at least two of the circles intersect?
![]()
Solution
For any given pair of circles, they can intersect at most ![]() times. Since there are
times. Since there are  pairs of circles, the maximum number of possible intersections is
pairs of circles, the maximum number of possible intersections is ![]() . We can construct such a situation as below, so the answer is
. We can construct such a situation as below, so the answer is ![]() .
.
See also
| 2002 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 13 |
Followed by Problem 15 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |