Difference between revisions of "2002 AMC 12A Problems/Problem 25"
(The solution) |
(→Problem) |
||
| Line 2: | Line 2: | ||
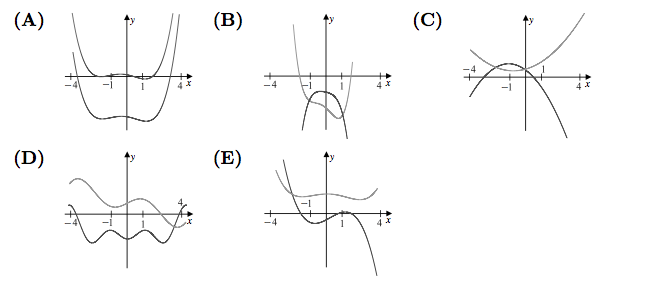
The nonzero coefficients of a polynomial <math>P</math> with real coefficients are all replaced by their mean to form a polynomial <math>Q</math>. Which of the following could be a graph of <math>y = P(x)</math> and <math>y = Q(x)</math> over the interval <math>-4\leq x \leq 4</math>? | The nonzero coefficients of a polynomial <math>P</math> with real coefficients are all replaced by their mean to form a polynomial <math>Q</math>. Which of the following could be a graph of <math>y = P(x)</math> and <math>y = Q(x)</math> over the interval <math>-4\leq x \leq 4</math>? | ||
| + | |||
| + | [[File:2002AMC12A25.png]] | ||
==Solution== | ==Solution== | ||
Revision as of 19:35, 26 January 2011
Problem
The nonzero coefficients of a polynomial 
with real coefficients are all replaced by their mean to form a polynomial 
. Which of the following could be a graph of 
and 
over the interval 
?
Solution
(B) The sum of the coefficients of and of will be equal, so 
. The only answer choice with an intersection at 
is at (B). (The polynomials in the graph are 
and 
.)
See Also
| 2002 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 24 |
Followed by Last Problem |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
