Difference between revisions of "Trigonometry"

Revision as of 13:34, 27 June 2006

Trigonometry seeks to find the lengths of a triangle's sides, given 2 angles and a side. Trigonometry is closely related to analytic geometry.

Basic definitions

Usually we call an angle $\displaystyle \theta$ , read "theta", but $\displaystyle \theta$ is just a variable. We could just as well call it $\displaystyle a$ .

For the following definitions, the "opposite side" is the side opposite of angle $\displaystyle \theta$ , and the "adjacent side" is the side that is part of angle $\displaystyle \theta$ , but is not the hypotenuse.

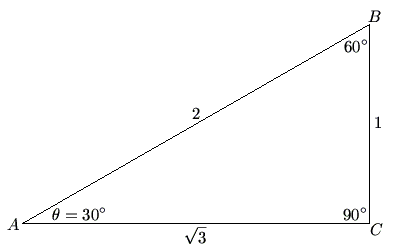
i.e. If ABC is a right triangle with right angle C, and angle A = $\displaystyle \theta$ , then BC is the "opposite side", AC is the "adjacent side", and AB is the hypotenuse.

Sine

The sine of an angle $\theta$ , abbreviated $\displaystyle \sin \theta$ , is the ratio between the opposite side and the hypotenuse of a triangle. For instance, in the 30-60-90 triangle above, $\sin 30=\frac 12$ .

Cosine

The cosine of an angle $\theta$ , abbreviated $\displaystyle \cos \theta$ , is the ratio between the adjacent side and the hypotenuse of a triangle. For instance, in the 30-60-90 triangle above, $\cos 30=\frac{\sqrt{3}}{2}$ .

Tangent

The tangent of an angle $\theta$ , abbreviated $\displaystyle \tan \theta$ , is the ratio between the opposite side and the adjacent side of a triangle. For instance, in the 30-60-90 triangle above, $\tan 30=\frac{\sqrt{3}}{3}$ . (Note that $\tan \theta=\frac{\sin\theta}{\cos\theta}$ .)

Cosecant

The cosecant of an angle $\theta$ , abbreviated $\displaystyle \csc \theta$ , is the ratio between the hypotenuse and the opposite side of a triangle. For instance, in the 30-60-90 triangle above, $\displaystyle \csc 30=2$ . (Note that $\csc \theta=\frac{1}{\sin \theta}$ .)

Secant

The secant of an angle $\theta$ , abbreviated $\displaystyle \sec \theta$ , is the ratio between the hypotenuse and the adjacent side of a triangle. For instance, in the 30-60-90 triangle above, $\sec 30=\frac{2\sqrt{3}}{3}$ . (Note that $\sec \theta=\frac{1}{\cos \theta}$ .)

Cotangent

The cotangent of an angle $\theta$ , abbreviated $\displaystyle \cot \theta$ , is the ratio between the adjacent side and the opposite side of a triangle. For instance, in the 30-60-90 triangle above, $\cot 30=\sqrt{3}$ . (Note that $\cot \theta=\frac{\cos\theta}{\sin\theta}$ .)

Trigonometery Definitions for non-acute angles

Consider a unit circle that is centered at the origin. By picking a point on the circle, and dropping a perpendicular line to the x-axis, a right triangle is formed with a hypotenuse 1 unit long. Letting the angle at the origin be $\displaystyle \theta$ and the coordinates of the point we picked to be $\displaystyle (x,y)$ , we have:

$\displaystyle \sin \theta = y$

$\displaystyle \cos \theta = x$

$\displaystyle \tan \theta = \frac{y}{x}$

$\displaystyle \csc \theta = \frac{1}{y}$

$\displaystyle \sec \theta = \frac{1}{x}$

$\displaystyle \cot \theta = \frac{x}{y}$

Note that $\displaystyle (x,y)$ is the rectangular coordinates for the point $(1,\theta)$ .

This is true for all angles, even negative angles and angles greater than 360 degrees. Due to the way trig ratios are defined for non-acute angles, the value of a trig ratio could be positive or negative, or even 0.

@@ Line 4: / Line 4: @@
 Usually we call an angle <math>\displaystyle \theta</math>, read "theta", but <math> \displaystyle \theta</math> is just a variable. We could just as well call it <math> \displaystyle  a</math>.
-For the following definitions, the "opposite side" is the side opposite of angle <math>\displaystyle \theta</math> and the "adjacent side" is the side that is part of angle <math>\displaystyle \theta</math> but is not the hypotenuse.
+For the following definitions, the "opposite side" is the side opposite of angle <math>\displaystyle \theta</math>, and the "adjacent side" is the side that is part of angle <math>\displaystyle \theta</math>, but is not the hypotenuse.
 i.e. If ABC is a right triangle with right angle C, and angle A = <math>\displaystyle \theta</math>, then BC is the "opposite side", AC is the "adjacent side", and AB is the hypotenuse.
@@ Line 30: / Line 30: @@
 ==Trigonometery Definitions for non-acute angles==
-Consider a [[unit circle]] that is centered at the origin. By picking a point on the circle, and dropping a perpendicular line to the x-axis, a right triangle is formed with a [[hypotenuse]] 1 unit long. Letting the angle at the origin be <math> \displaystyle \theta </math> and the coordinates of the point we picked to be <math> \displaystyle (x,y) </math> we have:
+Consider a [[unit circle]] that is centered at the origin. By picking a point on the circle, and dropping a perpendicular line to the x-axis, a right triangle is formed with a [[hypotenuse]] 1 unit long. Letting the angle at the origin be <math> \displaystyle \theta </math> and the coordinates of the point we picked to be <math> \displaystyle (x,y) </math>, we have:
 <math> \displaystyle \sin \theta = y </math>
@@ Line 44: / Line 44: @@
 <math> \displaystyle \cot \theta = \frac{x}{y} </math>
-Note that <math> \displaystyle (x,y) </math> is the rectangular coordinates for the point <math> (1,\theta) </math>
+Note that <math> \displaystyle (x,y) </math> is the rectangular coordinates for the point <math> (1,\theta) </math>.
-This is true for all angles (Even negative angles and angles greater than 360 degrees.) Due to the way trig ratios are defined for non acute angles, the value of a trig ratio could be positive of negative or even 0.
+This is true for all angles, even negative angles and angles greater than 360 degrees. Due to the way trig ratios are defined for non-acute angles, the value of a trig ratio could be positive or negative, or even 0.
 ==See also==
 * [[Trigonometric identities]]
 * [[Trigonometric substitution]]
 * [[Geometry]]

Page

Toolbox

Search