2022 AIME I Problems/Problem 15

Problem

Let $x,$ $y,$ and $z$ be positive real numbers satisfying the system of equations: $\begin{align*} \sqrt{2x-xy} + \sqrt{2y-xy} &= 1 \\ \sqrt{2y-yz} + \sqrt{2z-yz} &= \sqrt2 \\ \sqrt{2z-zx} + \sqrt{2x-zx} &= \sqrt3. \end{align*}$ Then $\left[ (1-x)(1-y)(1-z) \right]^2$ can be written as $\frac{m}{n},$ where $m$ and $n$ are relatively prime positive integers. Find $m+n.$

Solution 1 (geometric interpretation)

First, we note that we can let a triangle exist with side lengths $\sqrt{2x}$ , $\sqrt{2z}$ , and opposite altitude $\sqrt{xz}$ . This shows that the third side, which is the nasty square-rooted sum, is going to have the length equal to the sum on the right - let this be $l$ for symmetry purposes. So, we note that if the angle opposite the side with length $\sqrt{2x}$ has a value of $\sin(\theta)$ , then the altitude has length $\sqrt{2z} \cdot \sin(\theta) = \sqrt{xz}$ and thus $\sin(\theta) = \sqrt{\frac{x}{2}}$ so $x=2\sin^2(\theta)$ and the triangle side with length $\sqrt{2x}$ is equal to $2\sin(\theta)$ .

We can symmetrically apply this to the two other triangles, and since by law of sines, we have $\frac{2\sin(\theta)}{\sin(\theta)} = 2R \to R=1$ is the circumradius of that triangle. Hence. we calculate that with $l=1, \sqrt{2}$ , and $\sqrt{3}$ , the angles from the third side with respect to the circumcenter are $120^{\circ}, 90^{\circ}$ , and $60^{\circ}$ . This means that by half angle arcs, we see that we have in some order, $x=2\sin^2(\alpha)$ , $x=2\sin^2(\beta)$ , and $z=2\sin^2(\gamma)$ (not necessarily this order, but here it does not matter due to symmetry), satisfying that $\alpha+\beta=180^{\circ}-\frac{120^{\circ}}{2}$ , $\beta+\gamma=180^{\circ}-\frac{90^{\circ}}{2}$ , and $\gamma+\alpha=180^{\circ}-\frac{60^{\circ}}{2}$ . Solving, we get $\alpha=\frac{135^{\circ}}{2}$ , $\beta=\frac{105^{\circ}}{2}$ , and $\gamma=\frac{165^{\circ}}{2}$ .

We notice that $[(1-x)(1-y)(1-z)]^2=[\sin(2\alpha)\sin(2\beta)\sin(2\gamma)]^2=[\sin(135^{\circ})\sin(105^{\circ})\sin(165^{\circ})]^2$ $=\left(\frac{\sqrt{2}}{2} \cdot \frac{\sqrt{6}-\sqrt{2}}{4} \cdot \frac{\sqrt{6}+\sqrt{2}}{4}\right)^2 = \left(\frac{\sqrt{2}}{8}\right)^2=\frac{1}{32} \to \boxed{033}. \blacksquare$

- kevinmathz

Solution 2 (Detailed Geometric Solution created by ChatGPT)

To solve this problem, we use the fact that the three equations in the problem describe the lengths of the sides of three triangles that all share the same circumradius. This means that the circumradius is equal to 1, and so the circumcenter of these triangles is the origin.

We label the three triangles as $\triangle ABC$ , $\triangle BCD$ , and $\triangle CDA$ , where $A$ , $B$ , $C$ , and $D$ are the vertices of the triangles. Let the lengths of the sides opposite to vertices $A$ , $B$ , and $C$ be $\sqrt{2x}$ , $\sqrt{2y}$ , and $\sqrt{2z}$ , respectively. We also let the lengths of the sides of the triangles be $l_1$ , $l_2$ , and $l_3$ , respectively.

From the problem, we have the equations $l_1 = 1$ , $l_2 = \sqrt{2}$ , and $l_3 = \sqrt{3}$ . By the Pythagorean Theorem, we can express the lengths of the sides of the triangles as follows:

$l_1^2 = \sqrt{2x}^2 + \sqrt{2y}^2 - 2 \cdot \sqrt{2x} \cdot \sqrt{2y} \cdot \cos{\angle A}$ $l_2^2 = \sqrt{2y}^2 + \sqrt{2z}^2 - 2 \cdot \sqrt{2y} \cdot \sqrt{2z} \cdot \cos{\angle B}$ $l_3^2 = \sqrt{2z}^2 + \sqrt{2x}^2 - 2 \cdot \sqrt{2z} \cdot \sqrt{2x} \cdot \cos{\angle C}$

Since the circumradius of these triangles is 1, the lengths of the sides of the triangles are equal to the circumradius times the sines of the angles opposite to those sides. This means that

$l_1 = 1 \cdot \sin{\angle A}$ $l_2 = 1 \cdot \sin{\angle B}$ $l_3 = 1 \cdot \sin{\angle C}$

Substituting these expressions into the equations above and rearranging them, we get

$\sin^2{\angle A} = \frac{xy}{2x-xy}$ $\sin^2{\angle B} = \frac{yz}{2y-yz}$ $\sin^2{\angle C} = \frac{zx}{2z-zx}$

Since $x, y, z > 0$ , we can divide both sides of these equations by $x$ , $y$ , and $z$ , respectively, to get

$\sin^2{\angle A} = \frac{y}{2-y}$ $\sin^2{\angle B} = \frac{z}{2-z}$ $\sin^2{\angle C} = \frac{x}{2-x}$

Since the angles of the triangles are acute, we have $0 < \sin^2{\angle A}, \sin^2{\angle B}, \sin^2{\angle C} < 1$ . This means that $0 < y < 2$ , $0 < z < 2$ , and $0 < x < 2$ .

Since the angles of the triangles sum to $180^\circ$ , we have $\angle A + \angle B + \angle C = 180^\circ$ . Substituting the expressions for $\sin^2{\angle A}$ , $\sin^2{\angle B}$ , and $\sin^2{\angle C}$ into this equation and simplifying, we get [\frac{y}{2-y} + \frac{z}{2-z} + \frac{x}{2-x} = 1] Solving this equation, we get $x = \frac{4}{5}$ , $y = \frac{3}{4}$ , and $z = \frac{3}{5}$ .

Substituting these values into the expression $\left[ (1-x)(1-y)(1-z) \right]^2$ , we get [\left[ (1 - \frac{4}{5})(1 - \frac{3}{4})(1 - \frac{3}{5}) \right]^2 = \left[ \frac{1}{5} \cdot \frac{1}{4} \cdot \frac{2}{5} \right]^2 = \frac{1}{32}] Thus, the final answer is $m + n = 1 + 32 = \boxed{033}$ .

~ pi_is_3.14

Solution 2 (pure algebraic trig, easy to follow)

(This eventually whittles down to the same concept as Solution 1)

Note that in each equation in this system, it is possible to factor $\sqrt{x}$ , $\sqrt{y}$ , or $\sqrt{z}$ from each term (on the left sides), since each of $x$ , $y$ , and $z$ are positive real numbers. After factoring out accordingly from each terms one of $\sqrt{x}$ , $\sqrt{y}$ , or $\sqrt{z}$ , the system should look like this: $\begin{align*} \sqrt{x}\cdot\sqrt{2-y} + \sqrt{y}\cdot\sqrt{2-x} &= 1 \\ \sqrt{y}\cdot\sqrt{2-z} + \sqrt{z}\cdot\sqrt{2-y} &= \sqrt2 \\ \sqrt{z}\cdot\sqrt{2-x} + \sqrt{x}\cdot\sqrt{2-z} &= \sqrt3. \end{align*}$ This should give off tons of trigonometry vibes. To make the connection clear, $x = 2\cos^2 \alpha$ , $y = 2\cos^2 \beta$ , and $z = 2\cos^2 \theta$ is a helpful substitution: $\begin{align*} \sqrt{2\cos^2 \alpha}\cdot\sqrt{2-2\cos^2 \beta} + \sqrt{2\cos^2 \beta}\cdot\sqrt{2-2\cos^2 \alpha} &= 1 \\ \sqrt{2\cos^2 \beta}\cdot\sqrt{2-2\cos^2 \theta} + \sqrt{2\cos^2 \theta}\cdot\sqrt{2-2\cos^2 \beta} &= \sqrt2 \\ \sqrt{2\cos^2 \theta}\cdot\sqrt{2-2\cos^2 \alpha} + \sqrt{2\cos^2 \alpha}\cdot\sqrt{2-2\cos^2 \theta} &= \sqrt3. \end{align*}$ From each equation $\sqrt{2}^2$ can be factored out, and when every equation is divided by 2, we get: $\begin{align*} \sqrt{\cos^2 \alpha}\cdot\sqrt{1-\cos^2 \beta} + \sqrt{\cos^2 \beta}\cdot\sqrt{1-\cos^2 \alpha} &= \frac{1}{2} \\ \sqrt{\cos^2 \beta}\cdot\sqrt{1-\cos^2 \theta} + \sqrt{\cos^2 \theta}\cdot\sqrt{1-\cos^2 \beta} &= \frac{\sqrt2}{2} \\ \sqrt{\cos^2 \theta}\cdot\sqrt{1-\cos^2 \alpha} + \sqrt{\cos^2 \alpha}\cdot\sqrt{1-\cos^2 \theta} &= \frac{\sqrt3}{2}. \end{align*}$ which simplifies to (using the Pythagorean identity $\sin^2 \phi + \cos^2 \phi = 1 \; \forall \; \phi \in \mathbb{C}$ ): $\begin{align*} \cos \alpha\cdot\sin \beta + \cos \beta\cdot\sin \alpha &= \frac{1}{2} \\ \cos \beta\cdot\sin \theta + \cos \theta\cdot\sin \beta &= \frac{\sqrt2}{2} \\ \cos \theta\cdot\sin \alpha + \cos \alpha\cdot\sin \theta &= \frac{\sqrt3}{2}. \end{align*}$ which further simplifies to (using sine addition formula $\sin(a + b) = \sin a \cos b + \cos a \sin b$ ): $\begin{align*} \sin(\alpha + \beta) &= \frac{1}{2} \\ \sin(\beta + \theta) &= \frac{\sqrt2}{2} \\ \sin(\alpha + \theta) &= \frac{\sqrt3}{2}. \end{align*}$ Without loss of generality, taking the inverse sine of each equation yields a simple system: $\begin{align*} \alpha + \beta &= \frac{\pi}{6} \\ \beta + \theta &= \frac{\pi}{4} \\ \alpha + \theta &= \frac{\pi}{3}. \end{align*}$ giving solutions $\alpha = \frac{\pi}{8}$ , $\beta = \frac{\pi}{24}$ , $\theta = \frac{5\pi}{24}$ . Since these unknowns are directly related to our original unknowns, there are consequent solutions for those: $x = 2\cos^2\left(\frac{\pi}{8}\right)$ , $y = 2\cos^2\left(\frac{\pi}{24}\right)$ , and $z = 2\cos^2\left(\frac{5\pi}{24}\right)$ . When plugging into the expression $\left[ (1-x)(1-y)(1-z) \right]^2$ , noting that $-\cos 2\phi = 1 - 2\cos^2 \phi\; \forall \; \phi \in \mathbb{C}$ helps to simplify this expression into: $\left[ (-1)^3\left(\cos \left(2\cdot\frac{\pi}{8}\right)\cos \left(2\cdot\frac{\pi}{24}\right)\cos \left(2\cdot\frac{5\pi}{24}\right)\right)\right]^2 = \left[ (-1)\left(\cos \left(\frac{\pi}{4}\right)\cos \left(\frac{\pi}{12}\right)\cos \left(\frac{5\pi}{12}\right)\right)\right]^2$ Now, all the cosines in here are fairly standard: $\cos \frac{\pi}{4} = \frac{\sqrt{2}}{2}$ , $\;$ $\cos \frac{\pi}{12} = \frac{\sqrt{6} + \sqrt{2}}{4}$ , $\;$ and $\cos \frac{5\pi}{12} = \frac{\sqrt{6} - \sqrt{2}}{4}$ . With some final calculations: $(-1)^2\left(\frac{\sqrt{2}}{2}\right)^2\left(\frac{\sqrt{6} + \sqrt{2}}{4}\right)^2\left(\frac{\sqrt{6} - \sqrt{2}}{4}\right)^2 = \left(\frac{1}{2}\right)\left(\frac{2 + \sqrt{3}}{4}\right)\left(\frac{2 - \sqrt{3}}{4}\right) = \frac{\left(2 - \sqrt{3}\right)\left(2 + \sqrt{3}\right)}{2\cdot4\cdot4} = \frac{1}{32}.$ This is our answer in simplest form $\frac{m}{n}$ , so $m + n = 1 + 32 = \boxed{033}.$

~Oxymoronic15

solution 3

Let $1-x=a;1-y=b;1-z=c$ , rewrite those equations

$\sqrt{(1-a)(1+b)}+\sqrt{(1+a)(1-b)}=1$ ;

$\sqrt{(1-b)(1+c)}+\sqrt{(1+b)(1-c)}=\sqrt{2}$

$\sqrt{(1-a)(1+c)}+\sqrt{(1-c)(1+a)}=\sqrt{3}$

square both sides, get three equations:

$2ab-1=2\sqrt{(1-a^2)(1-b^2)}$

$2bc=2\sqrt{(1-b^2)(1-c^2)}$

$2ac+1=2\sqrt{(1-c^2)(1-a^2)}$

Getting that $a^2+b^2-ab=\frac{3}{4}$

$b^2+c^2=1$

$a^2+c^2+ac=\frac{3}{4}$

Subtract first and third equation, getting $(b+c)(b-c)=a(b+c)$ , $a=b-c$

Put it in first equation, getting $b^2-2bc+c^2+b^2-b(b-c)=b^2+c^2-bc=\frac{3}{4}$ , $bc=\frac{1}{4}$

Since $a^2=b^2+c^2-2bc=\frac{1}{2}$ , the final answer is $\frac{1}{4}*\frac{1}{4}*\frac{1}{2}=\frac{1}{32}$ the final answer is $\boxed{033}$

~bluesoul

Solution 4

Denote $u = 1 - x$ , $v = 1 - y$ , $w = 1 - z$ . Hence, the system of equations given in the problem can be written as $\begin{align*} \sqrt{(1-u)(1+v)} + \sqrt{(1+u)(1-v)} & = 1 \hspace{1cm} (1) \\ \sqrt{(1-v)(1+w)} + \sqrt{(1+v)(1-w)} & = \sqrt{2} \hspace{1cm} (2) \\ \sqrt{(1-w)(1+u)} + \sqrt{(1+w)(1-u)} & = \sqrt{3} . \hspace{1cm} (3) \end{align*}$

Each equation above takes the following form: $\sqrt{(1-a)(1+b)} + \sqrt{(1+a)(1-b)} = k .$

Now, we simplify this equation by removing radicals.

Denote $p = \sqrt{(1-a)(1+b)}$ and $q = \sqrt{(1+a)(1-b)}$ .

Hence, the equation above implies $\left\{ \begin{array}{l} p + q = k \\ p^2 = (1-a)(1+b) \\ q^2 = (1+a)(1-b) \end{array} \right..$

Hence, $q^2 - p^2 = (1+a)(1-b) - (1-a)(1+b) = 2 (a-b)$ . Hence, $q - p = \frac{q^2 - p^2}{p+q} = \frac{2}{k} (a-b)$ .

Because $p + q = k$ and $q - p = \frac{2}{k} (a-b)$ , we get $q = \frac{a-b}{k} + \frac{k}{2}$ . Plugging this into the equation $q^2 = (1+a)(1-b)$ and simplifying it, we get $a^2 + \left( k^2 - 2 \right) ab + b^2 = k^2 - \frac{k^4}{4} .$

Therefore, the system of equations above can be simplified as $\begin{align*} u^2 - uv + v^2 & = \frac{3}{4} \\ v^2 + w^2 & = 1 \\ w^2 + wu + u^2 & = \frac{3}{4} . \end{align*}$

Denote $w' = - w$ . The system of equations above can be equivalently written as $\begin{align*} u^2 - uv + v^2 & = \frac{3}{4} \hspace{1cm} (1') \\ v^2 + w'^2 & = 1 \hspace{1cm} (2') \\ w'^2 - w'u + u^2 & = \frac{3}{4} \hspace{1cm} (3') . \end{align*}$

Taking $(1') - (3')$ , we get $(v - w') (v + w' - u) = 0 .$

Thus, we have either $v - w' = 0$ or $v + w' - u = 0$ .

$\textbf{Case 1}$ : $v - w' = 0$ .

Equation (2') implies $v = w' = \pm \frac{1}{\sqrt{2}}$ .

Plugging $v$ and $w'$ into Equation (2), we get contradiction. Therefore, this case is infeasible.

$\textbf{Case 2}$ : $v + w' - u = 0$ .

Plugging this condition into (1') to substitute $u$ , we get $v^2 + v w' + w'^2 = \frac{3}{4} \hspace{1cm} (4) .$

Taking $(4) - (2')$ , we get $v w' = - \frac{1}{4} . \hspace{1cm} (5) .$

Taking (4) + (5), we get $\left( v + w' \right)^2 = \frac{1}{2} .$

Hence, $u^2 = \left( v + w' \right)^2 = \frac{1}{2}$ .

Therefore, $\begin{align*} \left[ (1-x)(1-y)(1-z) \right]^2 & = u^2 (vw)^2 \\ & = u^2 (vw')^2 \\ & = \frac{1}{2} \left( - \frac{1}{4} \right)^2 \\ & = \frac{1}{32} . \end{align*}$

Therefore, the answer is $1 + 32 = \boxed{\textbf{(033) }}$ . \end{solution}

~Steven Chen (www.professorchenedu.com)

Solution 5

Let $a=1-x$ , $b=1-y$ , and $c=1-z$ . Then, $\begin{align*} \sqrt{(1-a)(1+b)} + \sqrt{(1+a)(1-b)} &= 1 \hspace{15mm}(1) \\ \sqrt{(1-b)(1+c)} + \sqrt{(1+b)(1-c)} &= \sqrt2 \hspace{11.5mm}(2) \\ \sqrt{(1-a)(1+c)} + \sqrt{(1+a)(1-c)} &= \sqrt3. \hspace{10.5mm}(3). \end{align*}$

Notice that $\frac{1-a}{2}+\frac{1+a}{2}=1$ , $\frac{1-b}{2}+\frac{1+b}{2}=1$ , and $\frac{1-c}{2}+\frac{1+c}{2}=1$ . Let $\sin^2(\alpha)=(1-a)/2$ , $\sin^2(\beta)=(1-b)/2$ , and $\sin^2(\gamma)=(1-c)/2$ where $\alpha$ , $\beta$ , and $\gamma$ are real. Substituting into $(1)$ , $(2)$ , and $(3)$ yields $\begin{align*} \sin(\alpha + \beta) &= 1/2 \\ \sin(\alpha + \gamma) &= \sqrt2/2 \\ \sin(\beta + \gamma) &= \sqrt3/2. \end{align*}$ Thus, $\begin{align*} \alpha + \beta &= 30^{\circ} \\ \alpha + \gamma &= 45^{\circ} \\ \beta + \gamma &= 60^{\circ}, \end{align*}$ so $(\alpha, \beta, \gamma) = (15/2^{\circ}, 45/2^{\circ}, 75/2^{\circ})$ . Hence,

$abc = (1-2\sin^2(\alpha))(1-2\sin^2(\beta))(1-2\sin^2(\gamma))=\cos(15^{\circ})\cos(45^{\circ})\cos(75^{\circ})=\frac{\sqrt{2}}{8},$ so $(abc)^2=(\sqrt{2}/8)^2=\frac{1}{32}$ , for a final answer of $\boxed{033}$ .

Remark

The motivation for the trig substitution is that if $\sin^2(\alpha)=(1-a)/2$ , then $\cos^2(\alpha)=(1+a)/2$ , and when making the substitution in each equation of the initial set of equations, we obtain a new equation in the form of the sine addition formula.

~ Leo.Euler

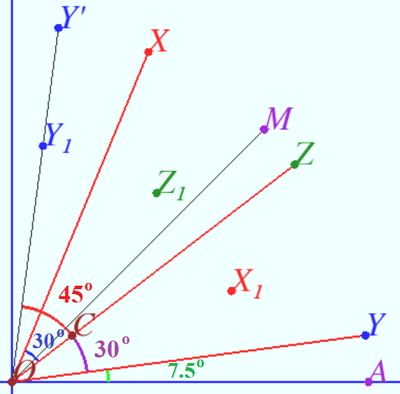
Solution 6 (Geometric)

In given equations, $0 \leq x,y,z \leq 2,$ so we define some points: $\bar {O} = (0, 0), \bar {A} = (1, 0), \bar{M} = \left(\frac {1}{\sqrt{2}},\frac {1}{\sqrt{2}}\right),$ $\bar {X} = \left(\sqrt {\frac {x}{2}}, \sqrt{1 – \frac{x}{2}}\right), \bar {Y'} = \left(\sqrt {\frac {y}{2}}, \sqrt{1 – \frac{y}{2}}\right),$ $\bar {Y} = \left(\sqrt {1 – \frac{y}{2}},\sqrt{\frac {y}{2}}\right), \bar {Z} = \left(\sqrt {1 – \frac{z}{2}},\sqrt{\frac {z}{2}}\right).$ Notice, that $\mid \vec {AO} \mid = \mid \vec {MO} \mid = \mid \vec {XO} \mid =\mid \vec {YO} \mid = \mid \vec {Y'O} \mid =\mid \vec {ZO} \mid = 1$ and each points lies in the first quadrant.

We use given equations and get some scalar products: $(\vec {XO} \cdot \vec {YO}) = \frac {1}{2} = \cos \angle XOY \implies \angle XOY = 60 ^\circ,$ $(\vec {XO} \cdot \vec {ZO}) = \frac {\sqrt{3}}{2} = \cos \angle XOZ \implies \angle XOZ = 30^\circ,$ $(\vec {Y'O} \cdot \vec {ZO}) = \frac {1}{\sqrt{2}} = \cos \angle Y'OZ \implies \angle Y'OZ = 45^\circ.$ So $\angle YOZ = \angle XOY – \angle XOZ = 60 ^\circ – 30 ^\circ = 30 ^\circ, \angle Y'OY = \angle Y'OZ + \angle YOZ = 45^\circ + 30 ^\circ = 75^\circ.$

Points $Y$ and $Y'$ are simmetric with respect to $OM.$

Case 1 $\angle YOA = \frac{90^\circ – 75^\circ}{2} = 7.5^\circ, \angle ZOA = 30^\circ + 7.5^\circ = 37.5^\circ, \angle XOA = 60^\circ + 7.5^\circ = 67.5^\circ .$ $1 – x = \left(\sqrt{1 – \frac{x}{2}} \right)^2– \left(\sqrt{\frac {x}{2}}\right)^2 = \sin^2 \angle XOA – \cos^2 \angle XOA = –\cos 2 \angle XOA = –\cos 135^\circ,$ $1 – y = \cos 15^\circ, 1 – z = \cos 75^\circ \implies \left[ (1–x)(1–y)(1–z) \right]^2 = \left[ \sin 45^\circ \cdot \cos 15^\circ \cdot \sin 15^\circ \right]^2 =$ $=\left[ \frac {\sin 45^\circ \cdot \sin 30^\circ}{2} \right]^2 = \frac {1}{32} \implies \boxed{\textbf{033}}.$ Case 2

$\angle Y_1 OA = \frac{90^\circ + 75^\circ}{2} = 82.5^\circ, \angle Z_1 OA = 82.5^\circ – 30^\circ = 52.5^\circ, \angle X_1 OA = 82.5^\circ – 60^\circ = 22.5^\circ \implies \boxed{\textbf{033}}.$

vladimir.shelomovskii@gmail.com, vvsss

Video Solution

https://www.youtube.com/watch?v=ihKUZ5itcdA

~Steven Chen (www.professorchenedu.com)

2022 AIME I (Problems • Answer Key • Resources)
Preceded by Problem 14	Followed by Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search