2005 AMC 12A Problems/Problem 16
Problem
Three circles of radius 
are drawn in the first quadrant of the 
-plane. The first circle is tangent to both axes, the second is tangent to the first circle and the 
-axis, and the third is tangent to the first circle and the 
-axis. A circle of radius 
is tangent to both axes and to the second and third circles. What is 
?
![[asy] unitsize(3mm); defaultpen(linewidth(.8pt)+fontsize(10pt)); dotfactor=3; pair O0=(9,9), O1=(1,1), O2=(3,1), O3=(1,3); pair P0=O0+9*dir(-45), P3=O3+dir(70); pair[] ps={O0,O1,O2,O3}; dot(ps); draw(Circle(O0,9)); draw(Circle(O1,1)); draw(Circle(O2,1)); draw(Circle(O3,1)); draw(O0--P0,linetype("3 3")); draw(O3--P3,linetype("2 2")); draw((0,0)--(18,0)); draw((0,0)--(0,18)); label("$r$",midpoint(O0--P0),NE); label("$s$",(-1.5,4)); draw((-1,4)--midpoint(O3--P3));[/asy]](http://latex.artofproblemsolving.com/6/5/7/657afd2eef0760abe2ccc3fe7453a83a0b22e681.png)
Solution
Solution 1
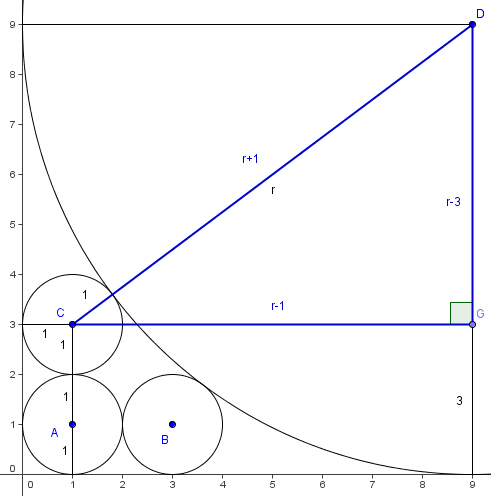
Set 
so that we only have to find 
. Draw the segment between the center of the third circle and the large circle; this has length 
. We then draw the radius of the large circle that is perpendicular to the x-axis, and draw the perpendicular from this radius to the center of the third circle. This gives us a right triangle with legs 
and hypotenuse . The Pythagorean Theorem yields:
Quite obviously 
, so 
.
Solution 2
Applying Wildin's Theorem directly yields
As before, , so .
~amkan2022
See also
| 2005 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 15 |
Followed by Problem 17 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
