2023 AMC 12B Problems/Problem 20

Problem

Cyrus the frog jumps $2$ units in a direction, then $2$ more in another direction. What is the probability that he lands less than $1$ unit away from his starting position?

$\textbf{(A)}~\frac{1}{6}\qquad\textbf{(B)}~\frac{1}{5}\qquad\textbf{(C)}~\frac{\sqrt{3}}{8}\qquad\textbf{(D)}~\frac{\arctan \frac{1}{2}}{\pi}\qquad\textbf{(E)}~\frac{2\arcsin \frac{1}{4}}{\pi}$

Solution 1

Let Cyrus's starting position be $S$ . WLOG, let the place Cyrus lands at for his first jump be $O$ . From $O$ , Cyrus can reach all the points on $\odot O$ . The probability that Cyrus will land less than $1$ unit away from $S$ is $\frac{4 \alpha }{ 2 \pi}$ .

$\sin \alpha = \frac{ \frac12 }{2} = \frac14, \quad \alpha = \arcsin \frac14$

Therefore, the answer is

$\frac{4 \arcsin \frac14 }{ 2 \pi} = \boxed{\textbf{(E) } \frac{2 \arcsin \frac{1}{4}}{\pi}}$

~isabelchen

Solution 2

Denote by $A_i$ the position after the $i$ th jump. Thus, to fall into the region centered at $A_0$ and with radius 1, $\angle A_2 A_1 A_0 < 2 \arcsin \frac{1/2}{2} = 2 \arcsin \frac{1}{4}$ .

Therefore, the probability is $\frac{2 \cdot 2 \arcsin \frac{1}{4}}{2 \pi} = \boxed{\textbf{(E) } \frac{2 \arcsin \frac{1}{4}}{\pi}}.$

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

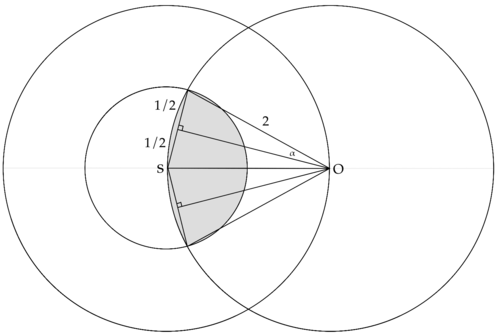
Solution 3(coord bash)

Let the orgin be the starting point of frog. Then, WLOG assume that after the first jump, it is at the point (2,0). Then, the range of all possible places the frog can jump to at its second jump is the circle with equation $(x-2)^2+y^2=2^2$ .If it landed $1$ unit within its starting point (the orgin), then it is inside the circle $x^2+y^2=1$ . We clearly want the intersection point. So we're trying to solve the system of equations $x^2+y^2=1$ and $(x-2)^2+y^2=2^2$ . We have $x=\frac{1}{4}$ , so $y=\pm\frac{\sqrt{15}}{4}$ . Therefore, our final answer would be $\frac{\arcsin{\frac{\sqrt{15}}{8}}}{\pi}$ (the angle we want divided by $2\pi$ ). But that is not one of our answer choices! Don't worry though, because

$\arcsin{\frac{\sqrt{15}}{8}}=\arccos{\frac{7}{8}}=\arccos{(1-2 \cdot (\frac{1}{4})^{2})}=2\arcsin{\frac{1}{4}}$

where the last step holds by the double angle formula. By now, it is clear that our answer is $\boxed{(E)\frac{2\arcsin{\frac{1}{4}}}{\pi}}$ . ~Ddk001

Solution 4 - Law of Cosines and Double Angle Formula

Let $A$ be Cyrus's starting point, $B$ be the first point he jumps to ( $AB = 2$ ), and $C$ be the second point he jumps to ( $BC = 2$ ). Let angle $ABC$ be $k$ , such that $AC = 1$ . The probability of $AC < 1$ would therefore be $\frac{2k}{360}$ (since $C$ could be on either side of $AB$ so there are two possible areas of having $AC < 1$ ) which simplifies to $\frac{k}{180}$ . Converting to radians gives us $\frac{k}{\pi}$ . To find $k$ , we use the law of cosines.

$AC^2 = AB^2 + BC^2 - 2 \cdot AB \cdot BC \cdot \cos k$ $1^2 = 2^2 + 2^2 - 2 \cdot 2 \cdot 2 \cdot \cos k$ $1 = 4 + 4 - 8 \cos k$ $8 \cos k = 7$ $\cos k = \frac{7}{8}$ $k = \arccos\left(\frac{7}{8}\right) = \arcsin\left(\sqrt{1 - \left(\frac{7}{8}\right)^2}\right) = \arcsin\left(\sqrt{\frac{15}{64}}\right) = \arcsin\left(\frac{1}{4} \sqrt{\frac{15}{4}}\right) = \arcsin\left(\frac{1}{4} \sqrt{1 - \left(\frac{1}{4}\right)^2}\right)$ $= \arcsin\left(\sin\left(\arcsin\left(\frac{1}{4}\right)\right) \cos\left(\arcsin\left(\frac{1}{4}\right)\right)\right) = \arcsin\left(\sin\left(2 \arcsin\left(\frac{1}{4}\right)\right)\right) = 2 \arcsin\left(\frac{1}{4}\right)$

The probability is $\frac{k}{\pi} = \frac{2 \arcsin\left(\frac{1}{4}\right)}{\pi}$

which is $E$ .

Video Solution 1 by OmegaLearn

https://youtu.be/nGZ9goJmg4Q

Video Solution

https://youtu.be/_i_d-C1cjyI

~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)

2023 AMC 12B (Problems • Answer Key • Resources)
Preceded by Problem 19	Followed by Problem 21
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search