2024 AMC 10A Problems/Problem 22
Problem
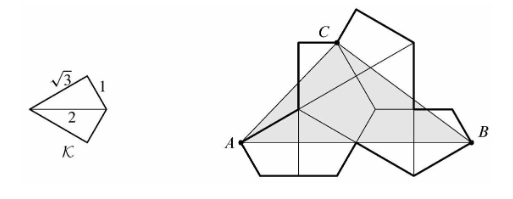
Let ![]() be the kite formed by joining two right triangles with legs
be the kite formed by joining two right triangles with legs ![]() and
and ![]() along a common hypotenuse. Eight copies of
along a common hypotenuse. Eight copies of ![]() are used to form the polygon shown below. What is the area of triangle
are used to form the polygon shown below. What is the area of triangle ![]() ?
?
![]()
Solution 1
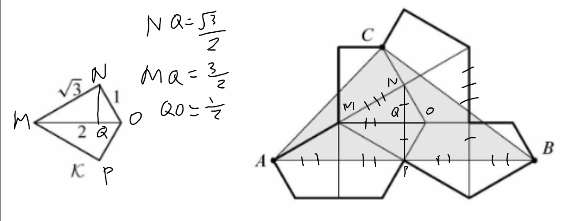
Let ![]() be quadrilateral MNOP. Drawing line MO splits the triangle into
be quadrilateral MNOP. Drawing line MO splits the triangle into ![]() .
Drawing the altitude from N to point Q on line MO, we know NQ is
.
Drawing the altitude from N to point Q on line MO, we know NQ is ![]() , MQ is
, MQ is ![]() , and QO is
, and QO is ![]() .
.
Due to the many similarities present, we can find that AB is ![]() , and the height of
, and the height of ![]() is
is ![]()
AB is ![]() and the height of
and the height of ![]() is
is ![]() .
.
Solving for the area of ![]() gives
gives ![]() which is
which is ![]()
~9897 (latex beginner here)
==Solution 2== (WIP)
~YTH (Working on it right now, please don't interfere. Thanks :) also if someone could help me create the solution 2 header that would be awesome)
See also
| 2024 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 21 |
Followed by Problem 23 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.