2024 AMC 10A Problems/Problem 22
Problem
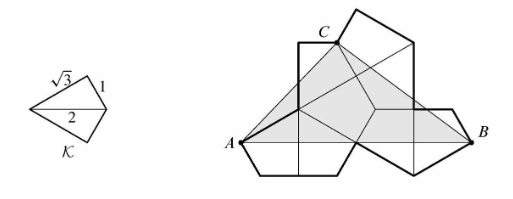
Let ![]() be the kite formed by joining two right triangles with legs
be the kite formed by joining two right triangles with legs ![]() and
and ![]() along a common hypotenuse. Eight copies of
along a common hypotenuse. Eight copies of ![]() are used to form the polygon shown below. What is the area of triangle
are used to form the polygon shown below. What is the area of triangle ![]() ?
?
![]()
Solution 1
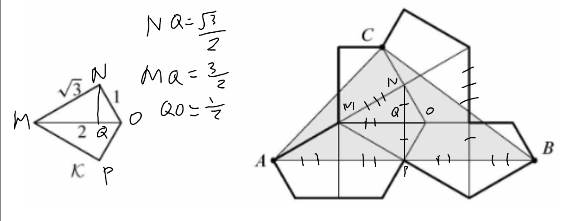
Let ![]() be quadrilateral MNOP. Drawing line MO splits the triangle into
be quadrilateral MNOP. Drawing line MO splits the triangle into ![]() .
Drawing the altitude from N to point Q on line MO, we know NQ is
.
Drawing the altitude from N to point Q on line MO, we know NQ is ![]() , MQ is
, MQ is ![]() , and QO is
, and QO is ![]() .
.
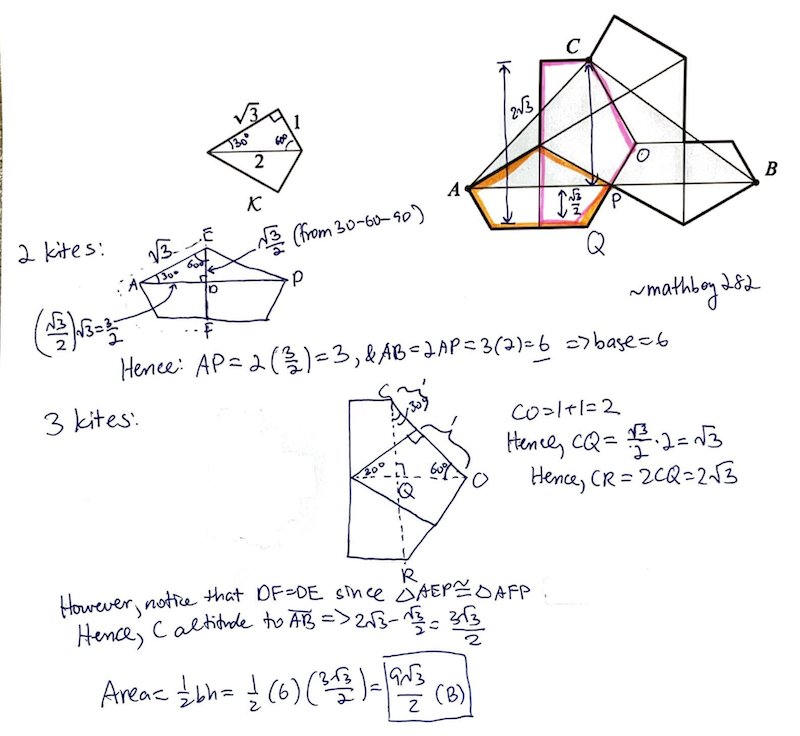
Due to the many similarities present, we can find that AB is ![]() , and the height of
, and the height of ![]() is
is ![]()
AB is ![]() and the height of
and the height of ![]() is
is ![]() .
.
Solving for the area of ![]() gives
gives ![]() which is
which is ![]()
~9897 (latex beginner here)
Solution 2
Let's start by looking at kite ![]() . We can quickly deduce based off of the side lengths that the kite can be split into two
. We can quickly deduce based off of the side lengths that the kite can be split into two ![]() triangles. Going back to the triangle
triangles. Going back to the triangle ![]() , focus on side
, focus on side ![]() . There are
. There are ![]() kites, they are all either reflected over the line
kites, they are all either reflected over the line ![]() or a line perpendicular to
or a line perpendicular to ![]() , meaning the length of
, meaning the length of ![]() can be split up into 4 equal parts.
can be split up into 4 equal parts.
Pick out the bottom-left kite, and we can observe that the kite and the triangle formed by the intersection of the kite and ![]() share a
share a ![]() degree angle. (this was deduced from the
degree angle. (this was deduced from the ![]() triangles in the kite) The line AB and the right side of the kite are perpendicular, forming a
triangles in the kite) The line AB and the right side of the kite are perpendicular, forming a ![]() angle. Because that is also a
angle. Because that is also a ![]() triangle with a hypotenuse of
triangle with a hypotenuse of ![]() , so we find the length of AB to be
, so we find the length of AB to be ![]() , which is
, which is ![]() .
.
Then, we can drop an altitude from ![]() to
to ![]() . We know that will be equivalent to the sum of the longer side of the kite and the shorter side of the triangle formed by the intersection of the kite and
. We know that will be equivalent to the sum of the longer side of the kite and the shorter side of the triangle formed by the intersection of the kite and ![]() . (Look at the line formed on the left of
. (Look at the line formed on the left of ![]() that drops down to
that drops down to ![]() if you are confused) We already have those values from the
if you are confused) We already have those values from the ![]() triangles, so we can just plug it into the triangle area formula,
triangles, so we can just plug it into the triangle area formula, ![]() . We get
. We get ![]()
~YTH (Need help with Latex and formatting)
~WIP (Header)
~Tacos_are_yummy_1 (![]() & Formatting)
& Formatting)
Solution 3
See also
| 2024 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 21 |
Followed by Problem 23 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.