2009 AMC 12B Problems/Problem 24

Problem

For how many values of $x$ in $[0,\pi]$ is $\sin^{ - 1}(\sin 6x) = \cos^{ - 1}(\cos x)$ ? Note: The functions $\sin^{ - 1} = \arcsin$ and $\cos^{ - 1} = \arccos$ denote inverse trigonometric functions.

$\textbf{(A)}\ 3\qquad \textbf{(B)}\ 4\qquad \textbf{(C)}\ 5\qquad \textbf{(D)}\ 6\qquad \textbf{(E)}\ 7$

Solution

First of all, we have to agree on the range of $\sin^{-1}$ and $\cos^{-1}$ . This should have been a part of the problem statement -- but as it is missing, we will assume the most common definition: $\forall x: -\pi/2 \leq \sin^{-1}(x) \leq \pi/2$ and $\forall x: 0\leq \cos^{-1}(x) \leq \pi$ .

Hence we get that $\forall x\in[0,\pi]: \cos^{ - 1}(\cos x) = x$ , thus our equation simplifies to $\sin^{ - 1}(\sin 6x) = x$ .

Consider the function $f(x) = \sin^{ - 1}(\sin 6x) - x$ . We are looking for roots of $f$ on $[0,\pi]$ .

By analyzing properties of $\sin$ and $\sin^{-1}$ (or by computing the derivative of $f$ ) one can discover the following properties of $f$ :

$f(0)=0$ .
$f$ is increasing and then decreasing on $[0,\pi/6]$ .
$f$ is decreasing and then increasing on $[\pi/6,2\pi/6]$ .
$f$ is increasing and then decreasing on $[2\pi/6,3\pi/6]$ .

For $x=\pi/6$ we have $f(x) = \sin^{-1} (\sin \pi) - \pi/6 = -\pi/6 < 0$ . Hence $f$ has exactly one root on $(0,\pi/6)$ .

For $x=2\pi/6$ we have $f(x) = \sin^{-1} (\sin 2\pi) - 2\pi/6 = -2\pi/6 < 0$ . Hence $f$ is negative on the entire interval $[\pi/6,2\pi/6]$ .

Now note that $\forall t: \sin^{-1}(t) \leq \pi/2$ . Hence for $x > 3\pi/6$ we have $f(x) < 0$ , and we can easily check that $f(3\pi/6)<0$ as well.

Thus the only unknown part of $f$ is the interval $(2\pi/6,3\pi/6)$ . On this interval, $f$ is negative in both endpoints, and we know that it is first increasing and then decreasing. Hence there can be zero, one, or two roots on this interval.

To prove that there are two roots, it is enough to find any $x$ from this interval such that $f(x)>0$ .

A good guess is its midpoint, $x=5\pi/12$ , where the function $\sin^{-1}(\sin 6x)$ has its local maximum. We can evaluate: $f(x) = \sin^{-1}(\sin 5\pi/2) - 5\pi/12 = \pi/2 - 5\pi/12 = \pi/12 > 0$ .

Summary: The function $f$ has $\boxed{\textbf{(B) }4}$ roots on $[0,\pi]$ : the first one is $0$ , the second one is in $(0,\pi/6)$ , and the last two are in $(2\pi/6,3\pi/6)$ .

Actual solutions are $x=0$ , $x=\pi/7$ , $x=2\pi/5$ , and $x=3\pi/7$ .

Solution 2

Since $0\leq \cos^{-1}(a) \leq \pi$ for all $a$ , the equation reduces to $\sin^{-1}(\sin(6x)) = x$ . Since $-\pi/2 \leq \sin^{-1}(a) \leq \pi/2$ for all $a$ , $0 \leq x \leq \pi/2$ . To make the problem easier, we will measure angles in degrees. We will consider each sixth of the interval $[0, 90]$ .

For $0 \leq x \leq 15$ , $6x$ is in the first quadrant. Thus, $\sin^{-1}(\sin(6x)) = 6x$ . Setting this equal to $x$ yields the solution $x = 0$ .

For $15 \leq x \leq 30$ , $6x$ is in the second quadrant. Thus, $\sin^{-1}(\sin(6x)) = 180 - 6x$ . This yields the solution $x = \frac{180}7$ .

For $30 \leq x \leq 45$ , $6x$ is in the third quadrant. Thus, $\sin^{-1}(\sin(6x)) = 180 - 6x$ . As $\frac{180}{7}$ is not on the interval $30 \leq x \leq 45$ , this yields no solution.

For $45 \leq x \leq 60$ , $6x$ is in the fourth quadrant. Thus, $\sin^{-1}(\sin(6x)) = 6x - 360$ . As $72$ is not on the interval $45 \leq x \leq 60$ , this yields no solution.

For $60 \leq x \leq 75$ , $6x$ is in the first quadrant plus a full revolution. Thus, $\sin^{-1}(\sin(6x)) = 6x - 360$ . This yields the solution $x = 72$ .

For $75 \leq x \leq 90$ , $6x$ is in the second quadrant plus a full revolution. Thus $\sin^{-1}(\sin(6x)) = 540 - 6x$ . This yields the solution $x = \frac{540}7$ .

There are $\boxed{\textbf{(B) }4}$ solutions, $x=0$ , $x=\pi/7$ , $x=2\pi/5$ , and $x=3\pi/7$ .

Solution 3

Algebraically, the inverse function of a function should just cancel out, leaving $6x=x$ . However, upon inspection we find that the graphs of these "inverse function of the function" equations are also periodic, like their normal trig function counterparts, due to the fact that inverse trig functions will never return any angle value higher than $2\pi$ . But instead of a smooth wave, these graphs are made up of zigzags with slope $1$ and $-1$ . Trying a few values, we see that

$y = \arcsin{\sin{x}}$

peaks at $\frac{\pi}{2}$ and

$y = \arccos{\cos{x}}$

peaks at $\pi$

But we want the graph of $y = \arcsin{(\sin6{x})}$ , which has a period of $\frac{\pi}{3}$ instead of $2\pi$ . So this means the interval $[0, \pi]$ will show $3$ periods instead of $\frac{1}{2}$ of a period. Visually it would be lines with slopes $6$ and $-6$ . Using the graph paper given to us, we plot out the two equations according to the above and we see that they intersect $4$ times $\Rightarrow \boxed{\text{B}}$ .

Solution 4

The most conventional domain and range for $\cos^{-1} x$ is $x \in [-1, 1]$ and $\cos^{-1} x \in [0, \pi]$ . For $\cos x$ , $x \in [0, \pi]$ and $\cos x \in [-1, 1]$ . Since the domain of $\cos x$ is equal to the range of $\cos^{-1} x$ , and the range of $\cos x$ is equal to the domain of $\cos^{-1} x$ , $\cos^{-1} (\cos x) = x$ .

Meaning that $\sin^{ - 1}(\sin 6x) = x$ , $\sin x = \sin (6x)$

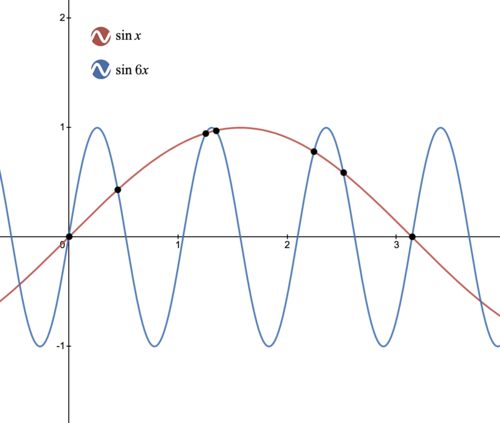
By graphing $\sin x$ and $\sin 6x$ together, it can be seen that they have 7 intersections within the range of $[0, \pi]$

However, the range of $\sin^{-1} x$ is $[-\frac{\pi}{2}, \frac{\pi}{2}]$ , meaning the intersections with a $x$ value more than $\frac{\pi}{2}$ is invalid. There are $\boxed{\textbf{(B) }4}$ solutions.

The $4$ solutions are respectively:

$x = 6x$ , $x = 0$

$x + 2 \pi = 6x$ , $x = \frac25 \pi$

$\pi - x = 6x$ , $x = \frac{\pi}{7}$

$3 \pi - x = 6x$ , $x = \frac37 \pi$

2009 AMC 12B (Problems • Answer Key • Resources)
Preceded by Problem 23	Followed by Problem 25
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

Page

Toolbox

Search