2024 AMC 10A Problems/Problem 22
Contents
[hide]Problem
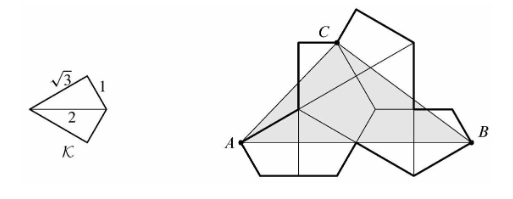
Let ![]() be the kite formed by joining two right triangles with legs
be the kite formed by joining two right triangles with legs ![]() and
and ![]() along a common hypotenuse. Eight copies of
along a common hypotenuse. Eight copies of ![]() are used to form the polygon shown below. What is the area of triangle
are used to form the polygon shown below. What is the area of triangle ![]() ?
?
![]()
Solution 1
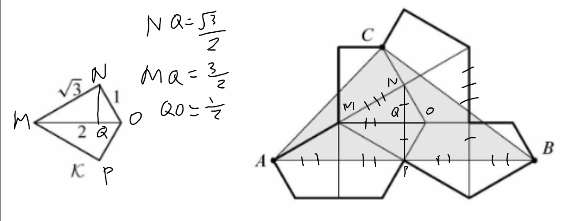
First, we should find the length of ![]() . In order to do this, as we see in the diagram, it can be split into 4 equal sections. Since diagram
. In order to do this, as we see in the diagram, it can be split into 4 equal sections. Since diagram ![]() shows us that it is made up of two
shows us that it is made up of two ![]() triangles, then the triangle outlined in red must be a
triangles, then the triangle outlined in red must be a ![]() triangle, as
triangle, as ![]() , and the two lines are perpendicular (is is proveable, but during competition, it is best to assume this is true, as the diagram is draw pretty well to scale). Also, since we know the length of the longest side is
, and the two lines are perpendicular (is is proveable, but during competition, it is best to assume this is true, as the diagram is draw pretty well to scale). Also, since we know the length of the longest side is ![]() , then the side we are looking for, which is outlined in blue, must be
, then the side we are looking for, which is outlined in blue, must be ![]() by the
by the ![]() relationship of
relationship of ![]() triangles. Therefore
triangles. Therefore ![]() , which is the base of the triangle we are looking, for must be {6}.
, which is the base of the triangle we are looking, for must be {6}.
Now all we have to do is find the height. We can split the height into 2 sections, the green and the light green. The green section must be ![]() , as
, as ![]() shows us. Also, the light green section must be equal to
shows us. Also, the light green section must be equal to ![]() , as in the previous paragraph, the triangle outlined in red is
, as in the previous paragraph, the triangle outlined in red is ![]() . Then, the green section, which is the height, must be
. Then, the green section, which is the height, must be ![]() , which is just
, which is just ![]() .
.
Then the area of the triangle must be ![]() , which is just
, which is just ![]()
~Solution by HappySharks ~Minor Edits by mathkiddus
Solution 2
Let ![]() be quadrilateral
be quadrilateral ![]() . Drawing line
. Drawing line ![]() splits the triangle into
splits the triangle into ![]() .
Drawing the altitude from
.
Drawing the altitude from ![]() to point
to point ![]() on line
on line ![]() , we know
, we know ![]() is
is ![]() ,
, ![]() is
is ![]() , and
, and ![]() is
is ![]() .
.
Due to the many similarities present, we can find that ![]() is
is ![]() , and the height of
, and the height of ![]() is
is ![]()
![]() is
is ![]() and the height of
and the height of ![]() is
is ![]() .
.
Solving for the area of ![]() gives
gives ![]() which is
which is ![]()
~9897 (latex beginner here)
~i_am_suk_at_math(very minor latex edits)
Solution 3
Let's start by looking at kite ![]() . We can quickly deduce based off of the side lengths that the kite can be split into two
. We can quickly deduce based off of the side lengths that the kite can be split into two ![]() triangles. Going back to the triangle
triangles. Going back to the triangle ![]() , focus on side
, focus on side ![]() . There are
. There are ![]() kites, they are all either reflected over the line
kites, they are all either reflected over the line ![]() or a line perpendicular to
or a line perpendicular to ![]() , meaning the length of
, meaning the length of ![]() can be split up into 4 equal parts.
can be split up into 4 equal parts.
Pick out the bottom-left kite, and we can observe that the kite and the triangle formed by the intersection of the kite and ![]() share a
share a ![]() degree angle. (this was deduced from the
degree angle. (this was deduced from the ![]() triangles in the kite) The line AB and the right side of the kite are perpendicular, forming a
triangles in the kite) The line AB and the right side of the kite are perpendicular, forming a ![]() angle. Because that is also a
angle. Because that is also a ![]() triangle with a hypotenuse of
triangle with a hypotenuse of ![]() , so we find the length of AB to be
, so we find the length of AB to be ![]() , which is
, which is ![]() .
.
Then, we can drop an altitude from ![]() to
to ![]() . We know that will be equivalent to the sum of the longer side of the kite and the shorter side of the triangle formed by the intersection of the kite and
. We know that will be equivalent to the sum of the longer side of the kite and the shorter side of the triangle formed by the intersection of the kite and ![]() . (Look at the line formed on the left of
. (Look at the line formed on the left of ![]() that drops down to
that drops down to ![]() if you are confused) We already have those values from the
if you are confused) We already have those values from the ![]() triangles, so we can just plug it into the triangle area formula,
triangles, so we can just plug it into the triangle area formula, ![]() . We get
. We get ![]()
~YTH (Need help with Latex and formatting)
~WIP (Header)
~Tacos_are_yummy_1 (![]() & Formatting)
& Formatting)
Solution 4 (On Paper)
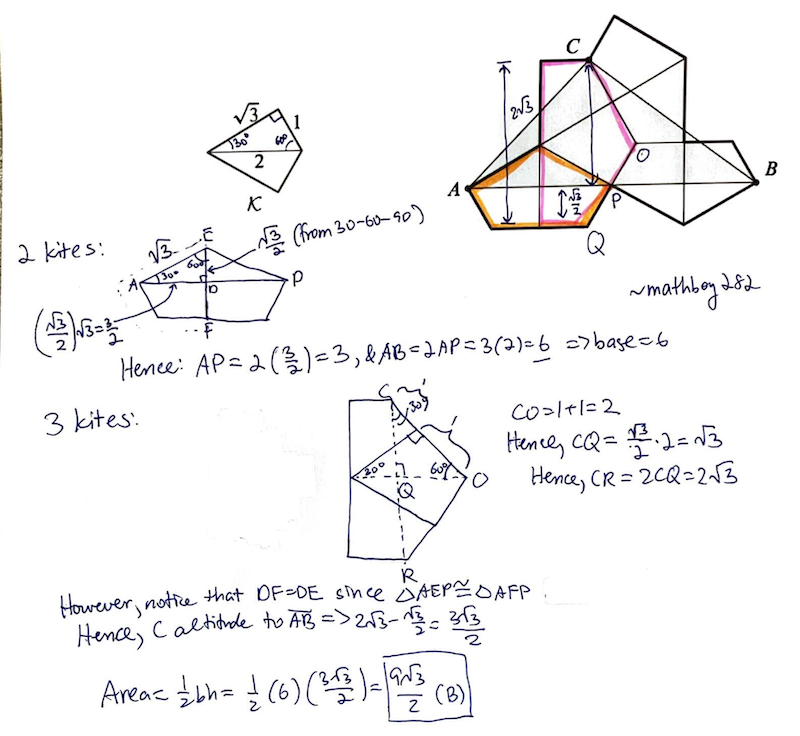 (latexing a WIP)
~mathboy282
~Thesmartgreekmathdude
(latexing a WIP)
~mathboy282
~Thesmartgreekmathdude
Solution 5
Let the point of intersection of ![]() and the kite with
and the kite with ![]() as vertex be
as vertex be ![]() .
.
Let the left kite with ![]() as a vertex touch the kite with
as a vertex touch the kite with ![]() as vertex at point
as vertex at point ![]() .
.
![]() is a
is a ![]() so
so ![]() and
and ![]() .
.
So, ![]() and
and ![]() , and the area is
, and the area is ![]()
~Mintylemon66
Solution 6(trig bash)
![]() As stated in the solutions above we can easily find that
As stated in the solutions above we can easily find that ![]() is split into
is split into ![]() equal parts, so we have
equal parts, so we have ![]() We can calculate
We can calculate ![]() by using
by using ![]() similarity to find
similarity to find ![]() is a
is a ![]() triangle, therefore we have
triangle, therefore we have ![]() and finally
and finally ![]() therefore
therefore ![]() Similarly we have
Similarly we have ![]() is congruent to
is congruent to ![]() therefore
therefore ![]() Next we have
Next we have ![]() is congruent to
is congruent to ![]() telling us
telling us ![]() Noticing
Noticing ![]() is right, we apply Pythagorean theorem to
is right, we apply Pythagorean theorem to ![]() to find
to find
![]()
![]()
![]()
![]() Next we would like to calculate CJ, As said before
Next we would like to calculate CJ, As said before ![]() so
so ![]() We know the inscribed angle between CG and GJ is
We know the inscribed angle between CG and GJ is ![]() and finally we know
and finally we know ![]() So we apply LoC on triangle CGJ in order to find CJ.
So we apply LoC on triangle CGJ in order to find CJ.
![]()
![]()
![]()
![]()
![]() Now since we have all side lengths of
Now since we have all side lengths of ![]() we can find
we can find ![]() Applying LoC again on
Applying LoC again on ![]() we have,
we have,
![]()
![]()
![]()
![]()
![]() We can solve for the area using the sin area formula which is
We can solve for the area using the sin area formula which is ![]() To find
To find ![]() we use the well known fact
we use the well known fact ![]() So we find,
So we find,
![]()
![]()
![]()
![]()
![]() Finally to wrap up we can find the area of
Finally to wrap up we can find the area of ![]() using the sin area formula,
using the sin area formula,
![]()
![]() Therefore our answer is
Therefore our answer is ![]() ~mathkiddus
~mathkiddus
Video Solution by Innovative Minds
https://www.youtube.com/watch?v=bhC58BB3kJA
~i_am_suk_at_math_2
See also
| 2024 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 21 |
Followed by Problem 23 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()