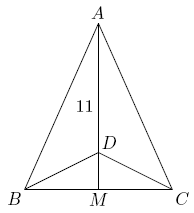
1995 AIME Problems/Problem 9
Problem
Triangle ![]() is isosceles, with
is isosceles, with ![]() and altitude
and altitude ![]() Suppose that there is a point
Suppose that there is a point ![]() on
on ![]() with
with ![]() and
and ![]() Then the perimeter of
Then the perimeter of ![]() may be written in the form
may be written in the form ![]() where
where ![]() and
and ![]() are integers. Find
are integers. Find ![]()
Solution
Let ![]() , $\angleCDM=3x$ (Error compiling LaTeX. Unknown error_msg). Then,
, $\angleCDM=3x$ (Error compiling LaTeX. Unknown error_msg). Then, ![]() . Expanding tan 3x using the angle sum formula gives
. Expanding tan 3x using the angle sum formula gives ![]() . Thus,
. Thus, ![]() . Solving, we get
. Solving, we get ![]() . Hence,
. Hence, ![]() and AC=
and AC=![]() by Pythag. The total perimeter is double the sum of these, which is
by Pythag. The total perimeter is double the sum of these, which is ![]() . The answer is then
. The answer is then ![]() .
.