2001 AMC 10 Problems/Problem 21
Contents
Problem
A right circular cylinder with its diameter equal to its height is inscribed in a right circular cone. The cone has diameter ![]() and altitude
and altitude ![]() , and the axes of the cylinder and cone coincide. Find the radius of the cylinder.
, and the axes of the cylinder and cone coincide. Find the radius of the cylinder.
![]()
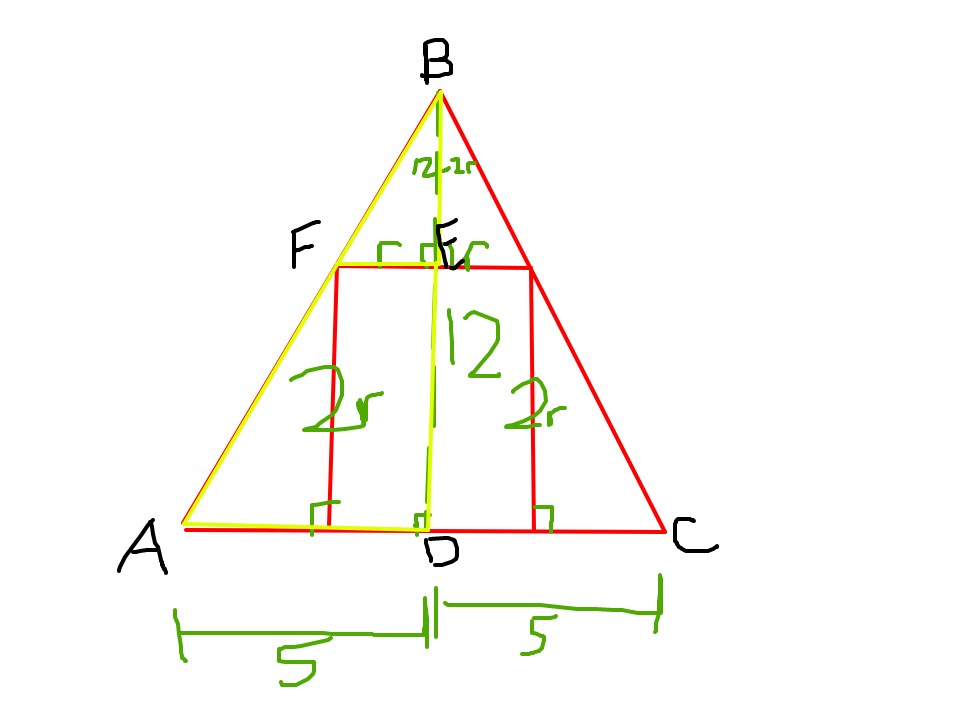
Solution 1
![[asy] draw((5,0)--(-5,0)--(0,12)--cycle); unitsize(.75cm); draw((-30/11,0)--(-30/11,60/11)); draw((-30/11,60/11)--(30/11,60/11)); draw((30/11,60/11)--(30/11,0)); draw((0,0)--(0,12)); label("$2r$",(0,30/11),E); label("$12-2r$",(0,80/11),E); label("$2r$",(0,60/11),S); label("$10$",(0,0),S); label("$A$",(0,12),N); label("$B$",(-5,0),SW); label("$C$",(5,0),SE); label("$D$",(-30/11,60/11),W); label("$E$",(30/11,60/11),E); [/asy]](http://latex.artofproblemsolving.com/8/a/4/8a48ba1b569474a4227381a6d073567c8d68ddf3.png)
Let the diameter of the cylinder be ![]() . Examining the cross section of the cone and cylinder, we find two similar triangles. Hence,
. Examining the cross section of the cone and cylinder, we find two similar triangles. Hence, ![]() which we solve to find
which we solve to find ![]() . Our answer is
. Our answer is ![]() .
.
Solution 2 (Very similar to solution 1 but explained more)
![]() :
:
We are asked to find the radius of the cylinder, or ![]() so we can look for similarity. We know that
so we can look for similarity. We know that ![]() and
and ![]() , thus we have similarity between
, thus we have similarity between ![]() and
and ![]() by
by ![]() similarity.
similarity.
Therefore, we can create an equation to find the length of the desired side. We know that:
![]()
Plugging in yields:
![]()
Cross multiplying and simplifying gives:
![]()
![]()
![]()
Since the problem asks us to find the radius of the cylinder, we are done and the radius of the cylinder is ![]() .
.
~etvat
See Also
| 2001 AMC 10 (Problems • Answer Key • Resources) | ||
| Preceded by Problem 20 |
Followed by Problem 22 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.