Difference between revisions of "2002 AMC 12B Problems/Problem 14"
(soln) |
5849206328x (talk | contribs) m |
||
| Line 9: | Line 9: | ||
== Solution == | == Solution == | ||
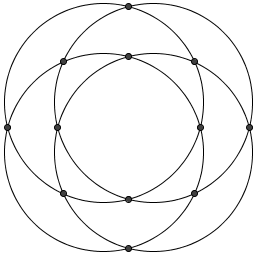
| − | For any given pair of circles, they can intersect at most <math>2</math> times. Since there are <math>{4\choose 2} = 6</math> circles, the maximum number of possible intersections is <math>6 \cdot 2 = 12</math>. We can construct such a situation as below, so the answer is <math>\mathrm{(D)}</math>. | + | For any given pair of circles, they can intersect at most <math>2</math> times. Since there are <math>{4\choose 2} = 6</math> pairs of circles, the maximum number of possible intersections is <math>6 \cdot 2 = 12</math>. We can construct such a situation as below, so the answer is <math>\mathrm{(D)}</math>. |
[[Image:2002_12B_AMC-14.png]] | [[Image:2002_12B_AMC-14.png]] | ||
Revision as of 22:01, 21 June 2009
Problem
Four distinct circles are drawn in a plane. What is the maximum number of points where at least two of the circles intersect?
Solution
For any given pair of circles, they can intersect at most 
times. Since there are 
pairs of circles, the maximum number of possible intersections is 
. We can construct such a situation as below, so the answer is 
.
See also
| 2002 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 13 |
Followed by Problem 15 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
