Difference between revisions of "2002 AMC 12B Problems/Problem 25"
| Line 9: | Line 9: | ||
\qquad\mathrm{(D)}\ 24 | \qquad\mathrm{(D)}\ 24 | ||
\qquad\mathrm{(E)}\ 25</math> | \qquad\mathrm{(E)}\ 25</math> | ||
| − | == Solution == | + | == Solution 1== |
The first condition gives us that | The first condition gives us that | ||
<cmath>x^2 + 6x + 1 + y^2 + 6y + 1 \le 0 \Longrightarrow (x+3)^2 + (y+3)^2 \le 16</cmath> | <cmath>x^2 + 6x + 1 + y^2 + 6y + 1 \le 0 \Longrightarrow (x+3)^2 + (y+3)^2 \le 16</cmath> | ||
| Line 28: | Line 28: | ||
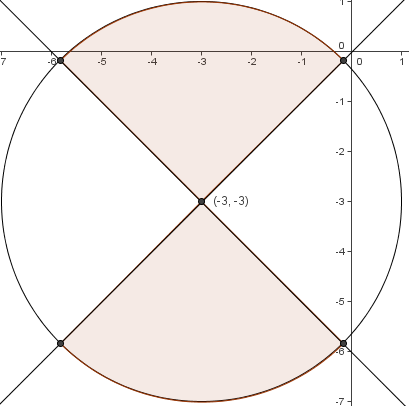
Each of those lines passes through <math>(-3,-3)</math> and has slope <math>\pm 1</math>, as shown above. Therefore, the area of <math>R</math> is half of the area of the circle, which is <math>\frac{1}{2} (\pi \cdot 4^2) = 8\pi \approx 25 \Rightarrow \mathrm{(E)}</math>. | Each of those lines passes through <math>(-3,-3)</math> and has slope <math>\pm 1</math>, as shown above. Therefore, the area of <math>R</math> is half of the area of the circle, which is <math>\frac{1}{2} (\pi \cdot 4^2) = 8\pi \approx 25 \Rightarrow \mathrm{(E)}</math>. | ||
| + | == Solution 2== | ||
| + | Similar to Solution 1, we proceed to get the area of the circle satisfying <math>f(x)+f(y) \le 0</math>, or <math>16 \pi</math>. | ||
| + | Since <math>f(x)-f(y) \le 0 \implies f(x) \le f(y)</math>, we have that by symmetry, if <math>(x,y)</math> is in <math>R</math>, then <math>(y,x)</math> is not, and vice versa. Therefore, the shaded part of the circle above the line <math>y=x</math> has the same area as the unshaded part below <math>y=x</math>, and the unshaded part above <math>y=x</math> has the same area as the shaded part below <math>y=x</math>. This means that exactly half the circle is shaded, allowing us to divide by two to get <math>\frac{16 \pi }{2} = \boxed{8 \pi}</math>. ~samrocksnature + ddot1 | ||
== See also == | == See also == | ||
{{AMC12 box|year=2002|ab=B|num-b=24|after=Last problem}} | {{AMC12 box|year=2002|ab=B|num-b=24|after=Last problem}} | ||
Revision as of 02:11, 3 March 2021
Contents
Problem
Let ![]() , and let
, and let ![]() denote the set of points
denote the set of points ![]() in the coordinate plane such that
in the coordinate plane such that
![]() The area of
The area of ![]() is closest to
is closest to
![]()
Solution 1
The first condition gives us that
![]()
which is a circle centered at ![]() with radius
with radius ![]() . The second condition gives us that
. The second condition gives us that
![]()
Thus either
![]()
or
![]()
Each of those lines passes through ![]() and has slope
and has slope ![]() , as shown above. Therefore, the area of
, as shown above. Therefore, the area of ![]() is half of the area of the circle, which is
is half of the area of the circle, which is ![]() .
.
Solution 2
Similar to Solution 1, we proceed to get the area of the circle satisfying ![]() , or
, or ![]() .
.
Since ![]() , we have that by symmetry, if
, we have that by symmetry, if ![]() is in
is in ![]() , then
, then ![]() is not, and vice versa. Therefore, the shaded part of the circle above the line
is not, and vice versa. Therefore, the shaded part of the circle above the line ![]() has the same area as the unshaded part below
has the same area as the unshaded part below ![]() , and the unshaded part above
, and the unshaded part above ![]() has the same area as the shaded part below
has the same area as the shaded part below ![]() . This means that exactly half the circle is shaded, allowing us to divide by two to get
. This means that exactly half the circle is shaded, allowing us to divide by two to get ![]() . ~samrocksnature + ddot1
. ~samrocksnature + ddot1
See also
| 2002 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 24 |
Followed by Last problem |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.