2005 AMC 12A Problems/Problem 16
Problem
Three circles of radius ![]() are drawn in the first quadrant of the
are drawn in the first quadrant of the ![]() -plane. The first circle is tangent to both axes, the second is tangent to the first circle and the
-plane. The first circle is tangent to both axes, the second is tangent to the first circle and the ![]() -axis, and the third is tangent to the first circle and the
-axis, and the third is tangent to the first circle and the ![]() -axis. A circle of radius
-axis. A circle of radius ![]() is tangent to both axes and to the second and third circles. What is
is tangent to both axes and to the second and third circles. What is ![]() ?
?
![]()
Solution
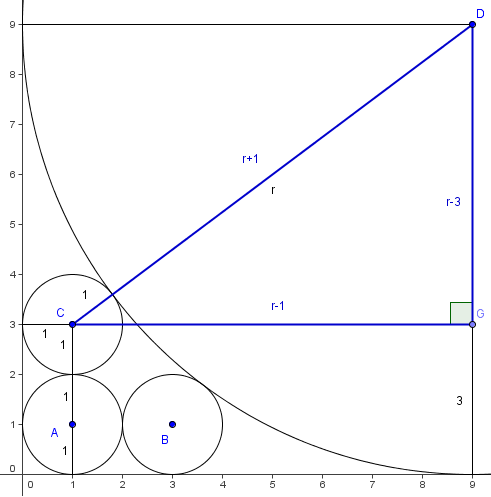
Without loss of generality, let ![]() . Draw the segment between the center of the third circle and the large circle; this has length
. Draw the segment between the center of the third circle and the large circle; this has length ![]() . We then draw the radius of the large circle that is perpendicular to the x-axis, and draw the perpendicular from this radius to the center of the third circle. This gives us a right triangle with legs
. We then draw the radius of the large circle that is perpendicular to the x-axis, and draw the perpendicular from this radius to the center of the third circle. This gives us a right triangle with legs ![]() and hypotenuse
and hypotenuse ![]() . The Pythagorean Theorem yields:
. The Pythagorean Theorem yields:
Quite obviously ![]() , so
, so ![]() and
and ![]() .
.
See also
| 2005 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 15 |
Followed by Problem 17 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |