Difference between revisions of "2013 AIME I Problems/Problem 13"
m (boxed the answer) |
(→Solution) |
||
| Line 3: | Line 3: | ||
== Solution == | == Solution == | ||
| − | Using Heron's Formula we can get the area of the triangle <math>\Delta AB_0C_0 = 90</math>. Since <math>\Delta AB_0C_0 \sim \Delta B_0C_1C_0 </math> then the scale factor for the dimensions of <math> \Delta B_0C_1C_0 </math> to <math>\Delta AB_0C_0 </math> is <math> \dfrac{17}{25}.</math> | + | Using Heron's Formula we can get the area of the triangle <math>\Delta AB_0C_0 = 90</math>. |
| + | |||
| + | Since <math>\Delta AB_0C_0 \sim \Delta B_0C_1C_0 </math> then the scale factor for the dimensions of <math> \Delta B_0C_1C_0 </math> to <math>\Delta AB_0C_0 </math> is <math> \dfrac{17}{25}.</math> | ||
| + | |||
Therefore, the area of <math> \Delta B_0C_1C_0 </math> is <math> (\dfrac{17}{25})^2(90) </math>. Also, the dimensions of the other sides of the <math> \Delta B_0C_1C_0 </math> can be | Therefore, the area of <math> \Delta B_0C_1C_0 </math> is <math> (\dfrac{17}{25})^2(90) </math>. Also, the dimensions of the other sides of the <math> \Delta B_0C_1C_0 </math> can be | ||
easily computed: <math> \overline{B_0C_1}= \dfrac{17}{25}(12) </math> and <math> \overline{C_1C_0} = \dfrac{17^2}{25} </math>. This allows us to compute one side of the | easily computed: <math> \overline{B_0C_1}= \dfrac{17}{25}(12) </math> and <math> \overline{C_1C_0} = \dfrac{17^2}{25} </math>. This allows us to compute one side of the | ||
Revision as of 10:33, 19 March 2017
Problem 13
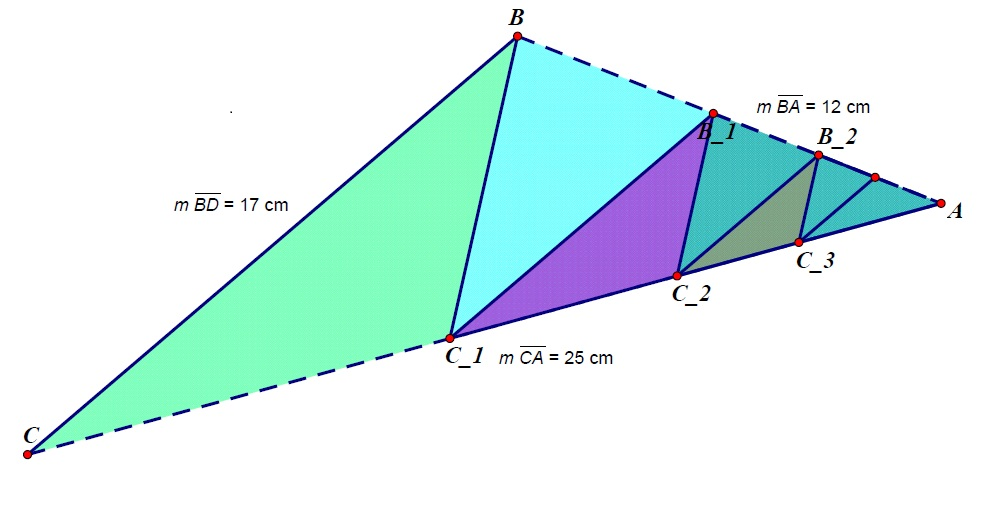
Triangle ![]() has side lengths
has side lengths ![]() ,
, ![]() , and
, and ![]() . For each positive integer
. For each positive integer ![]() , points
, points ![]() and
and ![]() are located on
are located on ![]() and
and ![]() , respectively, creating three similar triangles
, respectively, creating three similar triangles ![]() . The area of the union of all triangles
. The area of the union of all triangles ![]() for
for ![]() can be expressed as
can be expressed as ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Solution
Using Heron's Formula we can get the area of the triangle ![]() .
.
Since ![]() then the scale factor for the dimensions of
then the scale factor for the dimensions of ![]() to
to ![]() is
is ![]()
Therefore, the area of ![]() is
is ![]() . Also, the dimensions of the other sides of the
. Also, the dimensions of the other sides of the ![]() can be
easily computed:
can be
easily computed: ![]() and
and ![]() . This allows us to compute one side of the
triangle
. This allows us to compute one side of the
triangle ![]() ,
, ![]() . Therefore, the scale factor
. Therefore, the scale factor ![]() to
to ![]() is
is ![]() , which yields the length of
, which yields the length of ![]() as
as ![]() .
Therefore, the scale factor for
.
Therefore, the scale factor for ![]() to
to ![]() is
is ![]() . Some more algebraic manipulation will show that
. Some more algebraic manipulation will show that ![]() to
to ![]() is still
is still ![]() . Also, since the triangles are disjoint, the area of the union is the sum of the areas. Therefore, the area is the geometric series
. Also, since the triangles are disjoint, the area of the union is the sum of the areas. Therefore, the area is the geometric series
![]() At this point, it may be wise to "simplify"
At this point, it may be wise to "simplify" ![]() .
So the geometric series converges to
.
So the geometric series converges to
 .
Using the diffference of squares, we get
.
Using the diffference of squares, we get ![]() , which simplifies to
, which simplifies to ![]() . Cancellling all common factors, we get the reduced fraction
. Cancellling all common factors, we get the reduced fraction ![]() . So
. So ![]() , yielding the answer
, yielding the answer ![]() .
.
See also
| 2013 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 12 |
Followed by Problem 14 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.