Difference between revisions of "Conic section"
(images: standard equations) |
m (→Nondegenerate conic sections) |
||
| (16 intermediate revisions by 2 users not shown) | |||
| Line 8: | Line 8: | ||
* A [[circle]] is the conic section formed when the cutting plane is [[parallel]] to the [[base (geometry) | base]] of the cone or equivalently [[perpendicular]] to the axis. (This is really just a special case of the ellipse -- see the next bullet point.) | * A [[circle]] is the conic section formed when the cutting plane is [[parallel]] to the [[base (geometry) | base]] of the cone or equivalently [[perpendicular]] to the axis. (This is really just a special case of the ellipse -- see the next bullet point.) | ||
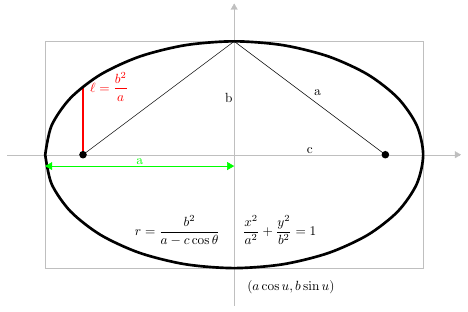
| − | * An [[ellipse]] is formed if the cutting plane makes an [[angle]] with | + | * An [[ellipse]] is formed if the cutting plane makes an [[angle]] with an [[axis]] that is larger than the angle between the slant height and the axis. |
| − | [[Image:Ellipse.png|alt=Ellipse]]By Klaas van Aarsen - Created as a latex tikzpicturePreviously published: Not published before, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=25261046 | + | |
| + | [[Image:Ellipse.png|alt=Ellipse]] | ||
| + | |||
| + | By Klaas van Aarsen - Created as a latex tikzpicturePreviously published: Not published before, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=25261046 | ||
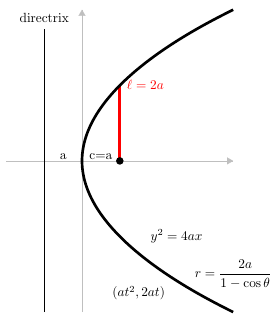
* A [[parabola]] is formed when the cutting plane makes an angle with the axis that is equal to the angle between the element of the cone and the axis. | * A [[parabola]] is formed when the cutting plane makes an angle with the axis that is equal to the angle between the element of the cone and the axis. | ||
| − | [[Image:Parabola2.png|alt=Parabola]]By Klaas van Aarsen - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=25261094 | + | [[Image:Parabola2.png|alt=Parabola]] |
| + | |||
| + | By Klaas van Aarsen - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=25261094 | ||
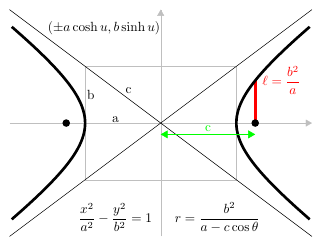
* An [[hyperbola]] is formed when the cutting plane makes an angle with the axis that is smaller than the angle between the element of the cone and the axis. | * An [[hyperbola]] is formed when the cutting plane makes an angle with the axis that is smaller than the angle between the element of the cone and the axis. | ||
| − | [[Image:Hyperbola.png|alt=Hyperbola]]By Klaas van Aarsen - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=25261095 | + | [[Image:Hyperbola.png|alt=Hyperbola]] |
| + | |||
| + | By Klaas van Aarsen - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=25261095 | ||
=== Degenerate conic sections === | === Degenerate conic sections === | ||
| Line 33: | Line 40: | ||
There are alternate (but equivalent) definitions of every conic section. We present them here: | There are alternate (but equivalent) definitions of every conic section. We present them here: | ||
| − | == Definitions of conic sections in terms of foci | + | == Definitions of conic sections in terms of a focus and a directrix == |
| − | + | *[[Circle]] - The locus of all points equidistant from a fixed point (i.e. the directrix is infinitely far from the origin)(<math>e = 0</math>). | |
| + | *[[Ellipse]] - The locus of all points where the distance from a line (the directrix) is some number <math>0 < e < 1</math> times the distance to some fixed point (the focus). | ||
| + | *[[Parabola]] - The locus of all points that are an equal distance away from a point (focus) and a line (called the directrix) (<math>e = 1</math>). | ||
| + | *[[Hyperbola]] - The locus of all points where the distance from a line (the directrix) is some number <math>e > 1</math> times the distance to some fixed point (the focus). | ||
| + | |||
| + | == Definitions of conic sections in terms of foci == | ||
| + | *[[Circle]] - The locus of all points equidistant from a fixed point (i.e. the two foci are the same point). | ||
| + | *[[Ellipse]] - The locus of all points where the sum of the distances to two points (the foci) is the same. | ||
| + | *[[Parabola]] - The locus of all points where the sum or difference of the distances to a point (the focus) and an infinitely far point (which can be replaced by a line) is the same. | ||
| + | *[[Hyperbola]] - The locus of all points where the absolute difference of the distances to two points (the foci) is the same. | ||
== Definitions of conic sections in terms of Cartesian coordinates == | == Definitions of conic sections in terms of Cartesian coordinates == | ||
| − | {{ | + | * [[Circle]] - <math>(x-h)^{2} + (y-k)^{2} = r^2</math>, where <math>(h,k)</math> is the [[center]] of the [[circle]], and <math>r</math> is the [[radius]] of the circle. |
| + | * [[Ellipse]] - <math>\frac{(x-h)^2}{a^2} + \frac{(y-k)^2}{b^2} = 1</math> or <math>\frac{(x-h)^2}{b^2} + \frac{(y-k)^2}{a^2} = 1</math>, where <math>(h,k)</math> is the [[center]] of the ellipse, <math>a</math> is the length of the [[semi-major axis]], and <math>b</math> is the length of the [[semi-minor axis]]. | ||
| + | * [[Parabola]] - <math>(x-h)^2 = 4p(y-k)</math> or <math>(y-k)^2 = 4p(x-h)</math>, where <math>(h,k)</math> is the [[vertex]] of the [[parabola]], and <math>p</math> is the distance between the [[focus]] and the [[vertex]]. (Also the distance from the [[vertex]] to the [[directrix]]). | ||
| + | * [[Hyperbola]] - <math>\frac{(x-h)^2}{a^2} - \frac{(y-k)^2}{b^2} = 1</math> or <math>\frac{(x-h)^2}{b^2} - \frac{(y-k)^2}{a^2} = 1</math>, where <math>(h,k)</math> is the [[center]] of the [[hyperbola]], <math>a</math> is the length of the [[semi-transverse axis]], and <math>b</math> is the length of the [[semi-conjugate axis]]. | ||
== See Also == | == See Also == | ||
Latest revision as of 01:14, 9 January 2023
A conic section is any of the geometric figures that can arise when a plane intersects a cone. (In fact, one usually considers a "two-ended cone," that is, two congruent right circular cones placed tip to tip so that their axes align.) As is clear from their definition, the conic sections are all plane curves, and every conic section can be described in Cartesian coordinates by a polynomial equation of degree two or less.
Contents
Classification of conic sections
All conic sections fall into the following categories:
Nondegenerate conic sections
- A circle is the conic section formed when the cutting plane is parallel to the base of the cone or equivalently perpendicular to the axis. (This is really just a special case of the ellipse -- see the next bullet point.)
- An ellipse is formed if the cutting plane makes an angle with an axis that is larger than the angle between the slant height and the axis.
By Klaas van Aarsen - Created as a latex tikzpicturePreviously published: Not published before, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=25261046
- A parabola is formed when the cutting plane makes an angle with the axis that is equal to the angle between the element of the cone and the axis.
By Klaas van Aarsen - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=25261094
- An hyperbola is formed when the cutting plane makes an angle with the axis that is smaller than the angle between the element of the cone and the axis.
By Klaas van Aarsen - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=25261095
Degenerate conic sections
If the cutting plane passes through the vertex of the cone, the result is a degenerate conic section. Degenerate conics fall into three categories:
- If the cutting plane makes an angle with the axis that is larger than the angle between the element of the cone and the axis then the plane intersects the cone only in the vertex, i.e. the resulting section is a single point. This is a degenerate ellipse.
- If the cutting plane makes an angle with the axis equal to the angle between the element of the cone and the axis then the plane is tangent to the cone and the resulting section is a line. This is a degenerate parabola.
- If the cutting plane makes an angle with the axis that is smaller than then angle between the element of the cone and the axis then the resulting section is two intersecting lines. This is a degenerate hyperbola.
An image is supposed to go here. You can help us out by creating one and editing it in. Thanks.
There are alternate (but equivalent) definitions of every conic section. We present them here:
Definitions of conic sections in terms of a focus and a directrix
- Circle - The locus of all points equidistant from a fixed point (i.e. the directrix is infinitely far from the origin)(
 ).
). - Ellipse - The locus of all points where the distance from a line (the directrix) is some number
 times the distance to some fixed point (the focus).
times the distance to some fixed point (the focus). - Parabola - The locus of all points that are an equal distance away from a point (focus) and a line (called the directrix) (
 ).
). - Hyperbola - The locus of all points where the distance from a line (the directrix) is some number
 times the distance to some fixed point (the focus).
times the distance to some fixed point (the focus).
Definitions of conic sections in terms of foci
- Circle - The locus of all points equidistant from a fixed point (i.e. the two foci are the same point).
- Ellipse - The locus of all points where the sum of the distances to two points (the foci) is the same.
- Parabola - The locus of all points where the sum or difference of the distances to a point (the focus) and an infinitely far point (which can be replaced by a line) is the same.
- Hyperbola - The locus of all points where the absolute difference of the distances to two points (the foci) is the same.
Definitions of conic sections in terms of Cartesian coordinates
- Circle -
 , where
, where  is the center of the circle, and
is the center of the circle, and  is the radius of the circle.
is the radius of the circle. - Ellipse -
 or
or  , where
, where  is the center of the ellipse,
is the center of the ellipse,  is the length of the semi-major axis, and
is the length of the semi-major axis, and  is the length of the semi-minor axis.
is the length of the semi-minor axis. - Parabola -
 or
or  , where
, where  is the vertex of the parabola, and
is the vertex of the parabola, and  is the distance between the focus and the vertex. (Also the distance from the vertex to the directrix).
is the distance between the focus and the vertex. (Also the distance from the vertex to the directrix). - Hyperbola -
 or
or  , where
, where  is the center of the hyperbola,
is the center of the hyperbola,  is the length of the semi-transverse axis, and
is the length of the semi-transverse axis, and  is the length of the semi-conjugate axis.
is the length of the semi-conjugate axis.