Conic section
A conic section is any of the geometric figures that can arise when a plane intersects a cone. (In fact, one usually considers a "two-ended cone," that is, two congruent right circular cones placed tip to tip so that their axes align.) As is clear from their definition, the conic sections are all plane curves, and every conic section can be described in Cartesian coordinates by a polynomial equation of degree two or less.
Contents
Classification of conic sections
All conic sections fall into the following categories:
Nondegenerate conic sections
- A circle is the conic section formed when the cutting plane is parallel to the base of the cone or equivalently perpendicular to the axis. (This is really just a special case of the ellipse -- see the next bullet point.)
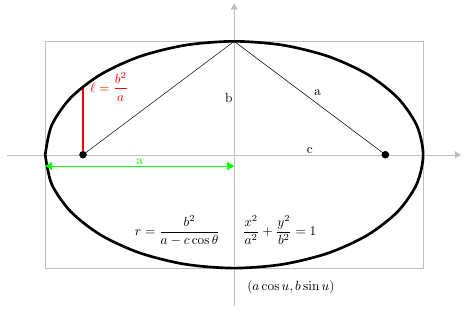
- An ellipse is formed if the cutting plane makes an angle with the axis that is larger than the angle between the element of the cone and the axis.
 By Klaas van Aarsen - Created as a latex tikzpicturePreviously published: Not published before, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=25261046
By Klaas van Aarsen - Created as a latex tikzpicturePreviously published: Not published before, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=25261046
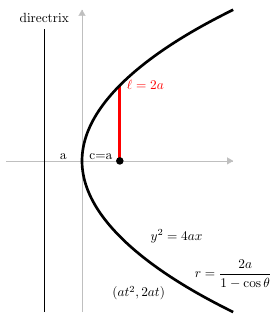
- A parabola is formed when the cutting plane makes an angle with the axis that is equal to the angle between the element of the cone and the axis.
 By Klaas van Aarsen - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=25261094
By Klaas van Aarsen - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=25261094
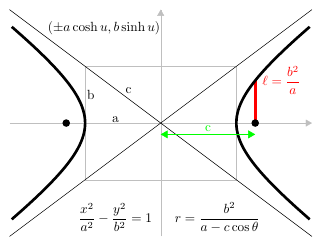
- An hyperbola is formed when the cutting plane makes an angle with the axis that is smaller than the angle between the element of the cone and the axis.
 By Klaas van Aarsen - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=25261095
By Klaas van Aarsen - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=25261095
Degenerate conic sections
If the cutting plane passes through the vertex of the cone, the result is a degenerate conic section. Degenerate conics fall into three categories:
- If the cutting plane makes an angle with the axis that is larger than the angle between the element of the cone and the axis then the plane intersects the cone only in the vertex, i.e. the resulting section is a single point. This is a degenerate ellipse.
- If the cutting plane makes an angle with the axis equal to the angle between the element of the cone and the axis then the plane is tangent to the cone and the resulting section is a line. This is a degenerate parabola.
- If the cutting plane makes an angle with the axis that is smaller than then angle between the element of the cone and the axis then the resulting section is two intersecting lines. This is a degenerate hyperbola.
An image is supposed to go here. You can help us out by creating one and editing it in. Thanks.
There are alternate (but equivalent) definitions of every conic section. We present them here:
Definitions of conic sections in terms of foci and directrices
Circle - The set of all points that are an equal distance away from a fixed point. Parabola - The set of all points that are an equal distance away from a point (called the focus) and a line (called the directrix). Ellipse - The set of all points in which the sum of the distances between two fixed points (called the foci) are the same. Hyperbola - The set of all points in which the difference of the distances between two fixed points (called the foci) are the same.
Definitions of conic sections in terms of Cartesian coordinates
This article is a stub. Help us out by expanding it.









