Difference between revisions of "User:Rowechen"
| Line 4: | Line 4: | ||
Here's the AIME compilation I will be doing: | Here's the AIME compilation I will be doing: | ||
| − | == Problem | + | == Problem 3 == |
| − | + | Sarah intended to multiply a two-digit number and a three-digit number, but she left out the multiplication sign and simply placed the two-digit number to the left of the three-digit number, thereby forming a five-digit number. This number is exactly nine times the product Sarah should have obtained. What is the sum of the two-digit number and the three-digit number? | |
| − | [[ | + | [[1997 AIME Problems/Problem 3|Solution]] |
| − | |||
| − | |||
| − | [[ | + | == Problem 5 == |
| − | == Problem | + | For certain real values of <math>a, b, c,</math> and <math>d_{},</math> the equation <math>x^4+ax^3+bx^2+cx+d=0</math> has four non-real roots. The product of two of these roots is <math>13+i</math> and the sum of the other two roots is <math>3+4i,</math> where <math>i=\sqrt{-1}.</math> Find <math>b.</math> |
| − | The | + | |
| − | < | + | [[1995 AIME Problems/Problem 5|Solution]] |
| − | are | + | |
| + | == Problem 4 == | ||
| + | In triangle <math>ABC</math>, angles <math>A</math> and <math>B</math> measure <math>60</math> degrees and <math>45</math> degrees, respectively. The bisector of angle <math>A</math> intersects <math>\overline{BC}</math> at <math>T</math>, and <math>AT=24</math>. The area of triangle <math>ABC</math> can be written in the form <math>a+b\sqrt{c}</math>, where <math>a</math>, <math>b</math>, and <math>c</math> are positive integers, and <math>c</math> is not divisible by the square of any prime. Find <math>a+b+c</math>. | ||
| + | |||
| + | [[2001 AIME I Problems/Problem 4|Solution]] | ||
| + | |||
| + | == Problem 9 == | ||
| + | A solitaire game is played as follows. Six distinct pairs of matched tiles are placed in a bag. The player randomly draws tiles one at a time from the bag and retains them, except that matching tiles are put aside as soon as they appear in the player's hand. The game ends if the player ever holds three tiles, no two of which match; otherwise the drawing continues until the bag is empty. The probability that the bag will be emptied is <math>p/q,\,</math> where <math>p\,</math> and <math>q\,</math> are relatively prime positive integers. Find <math>p+q.\,</math> | ||
| + | |||
| + | [[1994 AIME Problems/Problem 9|Solution]] | ||
| − | |||
== Problem 8 == | == Problem 8 == | ||
| − | + | For how many ordered pairs of positive integers <math>(x,y),</math> with <math>y<x\le 100,</math> are both <math>\frac xy</math> and <math>\frac{x+1}{y+1}</math> integers? | |
| + | |||
| + | [[1995 AIME Problems/Problem 8|Solution]] | ||
| − | + | == Problem 9 == | |
| − | == Problem | + | Triangle <math>ABC</math> is isosceles, with <math>AB=AC</math> and altitude <math>AM=11.</math> Suppose that there is a point <math>D</math> on <math>\overline{AM}</math> with <math>AD=10</math> and <math>\angle BDC=3\angle BAC.</math> Then the perimeter of <math>\triangle ABC</math> may be written in the form <math>a+\sqrt{b},</math> where <math>a</math> and <math>b</math> are integers. Find <math>a+b.</math> |
| − | |||
| − | < | ||
| − | < | ||
| − | |||
| − | [[ | + | [[Image:AIME_1995_Problem_9.png]] |
| − | |||
| − | |||
| − | [[ | + | [[1995 AIME Problems/Problem 9|Solution]] |
| − | |||
| − | |||
| − | |||
== Problem 11 == | == Problem 11 == | ||
| − | + | Let <math>\mathrm {P}</math> be the product of the roots of <math>z^6+z^4+z^3+z^2+1=0</math> that have a positive imaginary part, and suppose that <math>\mathrm {P}=r(\cos{\theta^{\circ}}+i\sin{\theta^{\circ}})</math>, where <math>0<r</math> and <math>0\leq \theta <360</math>. Find <math>\theta</math>. | |
| + | |||
| + | [[1996 AIME Problems/Problem 11|Solution]] | ||
| + | |||
| + | == Problem 13 == | ||
| + | Let <math>S</math> be the set of points in the Cartesian plane that satisfy <center><math>\Big|\big| |x|-2\big|-1\Big|+\Big|\big| |y|-2\big|-1\Big|=1.</math></center> If a model of <math>S</math> were built from wire of negligible thickness, then the total length of wire required would be <math>a\sqrt{b}</math>, where <math>a</math> and <math>b</math> are positive integers and <math>b</math> is not divisible by the square of any prime number. Find <math>a+b</math>. | ||
| + | |||
| + | [[1997 AIME Problems/Problem 13|Solution]] | ||
| − | |||
== Problem 12 == | == Problem 12 == | ||
| − | + | Let <math>ABC</math> be [[equilateral triangle|equilateral]], and <math>D, E,</math> and <math>F</math> be the [[midpoint]]s of <math>\overline{BC}, \overline{CA},</math> and <math>\overline{AB},</math> respectively. There exist [[point]]s <math>P, Q,</math> and <math>R</math> on <math>\overline{DE}, \overline{EF},</math> and <math>\overline{FD},</math> respectively, with the property that <math>P</math> is on <math>\overline{CQ}, Q</math> is on <math>\overline{AR},</math> and <math>R</math> is on <math>\overline{BP}.</math> The [[ratio]] of the area of triangle <math>ABC</math> to the area of triangle <math>PQR</math> is <math>a + b\sqrt {c},</math> where <math>a, b</math> and <math>c</math> are integers, and <math>c</math> is not divisible by the square of any [[prime]]. What is <math>a^{2} + b^{2} + c^{2}</math>? | |
| − | [[ | + | [[1998 AIME Problems/Problem 12|Solution]] |
| − | |||
| − | |||
| − | + | == Problem 11 == | |
| − | == Problem | + | Given that <math>\sum_{k=1}^{35}\sin 5k=\tan \frac mn,</math> where angles are measured in degrees, and <math>m_{}</math> and <math>n_{}</math> are relatively prime positive integers that satisfy <math>\frac mn<90,</math> find <math>m+n.</math> |
| − | |||
| − | [[ | + | [[1999 AIME Problems/Problem 11|Solution]] |
== Problem 14 == | == Problem 14 == | ||
| − | + | Point <math>P_{}</math> is located inside triangle <math>ABC</math> so that angles <math>PAB, PBC,</math> and <math>PCA</math> are all congruent. The sides of the triangle have lengths <math>AB=13, BC=14,</math> and <math>CA=15,</math> and the tangent of angle <math>PAB</math> is <math>m/n,</math> where <math>m_{}</math> and <math>n_{}</math> are relatively prime positive integers. Find <math>m+n.</math> | |
| − | [[ | + | [[1999 AIME Problems/Problem 14|Solution]] |
| − | == Problem | + | == Problem 14 == |
| − | In triangle <math>ABC</math> | + | In triangle <math>ABC,</math> it is given that angles <math>B</math> and <math>C</math> are congruent. Points <math>P</math> and <math>Q</math> lie on <math>\overline{AC}</math> and <math>\overline{AB},</math> respectively, so that <math>AP = PQ = QB = BC.</math> Angle <math>ACB</math> is <math>r</math> times as large as angle <math>APQ,</math> where <math>r</math> is a positive real number. Find the greatest integer that does not exceed <math>1000r</math>. |
| − | |||
| − | < | ||
| − | |||
| − | |||
| − | [[ | + | [[2000 AIME I Problems/Problem 14|Solution]] |
== Problem 15 == | == Problem 15 == | ||
| − | + | A stack of <math>2000</math> cards is labelled with the integers from <math>1</math> to <math>2000,</math> with different integers on different cards. The cards in the stack are not in numerical order. The top card is removed from the stack and placed on the table, and the next card is moved to the bottom of the stack. The new top card is removed from the stack and placed on the table, to the right of the card already there, and the next card in the stack is moved to the bottom of the stack. The process - placing the top card to the right of the cards already on the table and moving the next card in the stack to the bottom of the stack - is repeated until all cards are on the table. It is found that, reading from left to right, the labels on the cards are now in ascending order: <math>1,2,3,\ldots,1999,2000.</math> In the original stack of cards, how many cards were above the card labeled <math>1999</math>? | |
| + | [[2000 AIME I Problems/Problem 15|Solution]] | ||
| + | == Problem 14 == | ||
| + | Every positive integer <math>k</math> has a unique factorial base expansion <math>(f_1,f_2,f_3,\ldots,f_m)</math>, meaning that <math>k=1!\cdot f_1+2!\cdot f_2+3!\cdot f_3+\cdots+m!\cdot f_m</math>, where each <math>f_i</math> is an integer, <math>0\le f_i\le i</math>, and <math>0<f_m</math>. Given that <math>(f_1,f_2,f_3,\ldots,f_j)</math> is the factorial base expansion of <math>16!-32!+48!-64!+\cdots+1968!-1984!+2000!</math>, find the value of <math>f_1-f_2+f_3-f_4+\cdots+(-1)^{j+1}f_j</math>. | ||
| − | [[ | + | [[2000 AIME II Problems/Problem 14|Solution]] |
== Problem 13 == | == Problem 13 == | ||
| − | + | In a certain circle, the chord of a <math>d</math>-degree arc is 22 centimeters long, and the chord of a <math>2d</math>-degree arc is 20 centimeters longer than the chord of a <math>3d</math>-degree arc, where <math>d < 120.</math> The length of the chord of a <math>3d</math>-degree arc is <math>- m + \sqrt {n}</math> centimeters, where <math>m</math> and <math>n</math> are positive integers. Find <math>m + n.</math> | |
| − | [[ | + | [[2001 AIME I Problems/Problem 13|Solution]] |
Revision as of 14:35, 26 May 2020
Hey how did you get to this page? If you aren't me then I have to say hello. If you are me then I must be pretty conceited to waste my time looking at my own page. If you aren't me, seriously, how did you get to this page? This is pretty cool. Well, nice meeting you! I'm going to stop wasting my time typing this up and do some math. Gtg. Bye.
Here's the AIME compilation I will be doing:
Contents
Problem 3
Sarah intended to multiply a two-digit number and a three-digit number, but she left out the multiplication sign and simply placed the two-digit number to the left of the three-digit number, thereby forming a five-digit number. This number is exactly nine times the product Sarah should have obtained. What is the sum of the two-digit number and the three-digit number?
Problem 5
For certain real values of ![]() and
and ![]() the equation
the equation ![]() has four non-real roots. The product of two of these roots is
has four non-real roots. The product of two of these roots is ![]() and the sum of the other two roots is
and the sum of the other two roots is ![]() where
where ![]() Find
Find ![]()
Problem 4
In triangle ![]() , angles
, angles ![]() and
and ![]() measure
measure ![]() degrees and
degrees and ![]() degrees, respectively. The bisector of angle
degrees, respectively. The bisector of angle ![]() intersects
intersects ![]() at
at ![]() , and
, and ![]() . The area of triangle
. The area of triangle ![]() can be written in the form
can be written in the form ![]() , where
, where ![]() ,
, ![]() , and
, and ![]() are positive integers, and
are positive integers, and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]() .
.
Problem 9
A solitaire game is played as follows. Six distinct pairs of matched tiles are placed in a bag. The player randomly draws tiles one at a time from the bag and retains them, except that matching tiles are put aside as soon as they appear in the player's hand. The game ends if the player ever holds three tiles, no two of which match; otherwise the drawing continues until the bag is empty. The probability that the bag will be emptied is ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Problem 8
For how many ordered pairs of positive integers ![]() with
with ![]() are both
are both ![]() and
and ![]() integers?
integers?
Problem 9
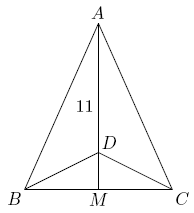
Triangle ![]() is isosceles, with
is isosceles, with ![]() and altitude
and altitude ![]() Suppose that there is a point
Suppose that there is a point ![]() on
on ![]() with
with ![]() and
and ![]() Then the perimeter of
Then the perimeter of ![]() may be written in the form
may be written in the form ![]() where
where ![]() and
and ![]() are integers. Find
are integers. Find ![]()
Problem 11
Let ![]() be the product of the roots of
be the product of the roots of ![]() that have a positive imaginary part, and suppose that
that have a positive imaginary part, and suppose that ![]() , where
, where ![]() and
and ![]() . Find
. Find ![]() .
.
Problem 13
Let ![]() be the set of points in the Cartesian plane that satisfy
be the set of points in the Cartesian plane that satisfy
If a model of ![]() were built from wire of negligible thickness, then the total length of wire required would be
were built from wire of negligible thickness, then the total length of wire required would be ![]() , where
, where ![]() and
and ![]() are positive integers and
are positive integers and ![]() is not divisible by the square of any prime number. Find
is not divisible by the square of any prime number. Find ![]() .
.
Problem 12
Let ![]() be equilateral, and
be equilateral, and ![]() and
and ![]() be the midpoints of
be the midpoints of ![]() and
and ![]() respectively. There exist points
respectively. There exist points ![]() and
and ![]() on
on ![]() and
and ![]() respectively, with the property that
respectively, with the property that ![]() is on
is on ![]() is on
is on ![]() and
and ![]() is on
is on ![]() The ratio of the area of triangle
The ratio of the area of triangle ![]() to the area of triangle
to the area of triangle ![]() is
is ![]() where
where ![]() and
and ![]() are integers, and
are integers, and ![]() is not divisible by the square of any prime. What is
is not divisible by the square of any prime. What is ![]() ?
?
Problem 11
Given that  where angles are measured in degrees, and
where angles are measured in degrees, and ![]() and
and ![]() are relatively prime positive integers that satisfy
are relatively prime positive integers that satisfy ![]() find
find ![]()
Problem 14
Point ![]() is located inside triangle
is located inside triangle ![]() so that angles
so that angles ![]() and
and ![]() are all congruent. The sides of the triangle have lengths
are all congruent. The sides of the triangle have lengths ![]() and
and ![]() and the tangent of angle
and the tangent of angle ![]() is
is ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Problem 14
In triangle ![]() it is given that angles
it is given that angles ![]() and
and ![]() are congruent. Points
are congruent. Points ![]() and
and ![]() lie on
lie on ![]() and
and ![]() respectively, so that
respectively, so that ![]() Angle
Angle ![]() is
is ![]() times as large as angle
times as large as angle ![]() where
where ![]() is a positive real number. Find the greatest integer that does not exceed
is a positive real number. Find the greatest integer that does not exceed ![]() .
.
Problem 15
A stack of ![]() cards is labelled with the integers from
cards is labelled with the integers from ![]() to
to ![]() with different integers on different cards. The cards in the stack are not in numerical order. The top card is removed from the stack and placed on the table, and the next card is moved to the bottom of the stack. The new top card is removed from the stack and placed on the table, to the right of the card already there, and the next card in the stack is moved to the bottom of the stack. The process - placing the top card to the right of the cards already on the table and moving the next card in the stack to the bottom of the stack - is repeated until all cards are on the table. It is found that, reading from left to right, the labels on the cards are now in ascending order:
with different integers on different cards. The cards in the stack are not in numerical order. The top card is removed from the stack and placed on the table, and the next card is moved to the bottom of the stack. The new top card is removed from the stack and placed on the table, to the right of the card already there, and the next card in the stack is moved to the bottom of the stack. The process - placing the top card to the right of the cards already on the table and moving the next card in the stack to the bottom of the stack - is repeated until all cards are on the table. It is found that, reading from left to right, the labels on the cards are now in ascending order: ![]() In the original stack of cards, how many cards were above the card labeled
In the original stack of cards, how many cards were above the card labeled ![]() ?
?
Problem 14
Every positive integer ![]() has a unique factorial base expansion
has a unique factorial base expansion ![]() , meaning that
, meaning that ![]() , where each
, where each ![]() is an integer,
is an integer, ![]() , and
, and ![]() . Given that
. Given that ![]() is the factorial base expansion of
is the factorial base expansion of ![]() , find the value of
, find the value of ![]() .
.
Problem 13
In a certain circle, the chord of a ![]() -degree arc is 22 centimeters long, and the chord of a
-degree arc is 22 centimeters long, and the chord of a ![]() -degree arc is 20 centimeters longer than the chord of a
-degree arc is 20 centimeters longer than the chord of a ![]() -degree arc, where
-degree arc, where ![]() The length of the chord of a
The length of the chord of a ![]() -degree arc is
-degree arc is ![]() centimeters, where
centimeters, where ![]() and
and ![]() are positive integers. Find
are positive integers. Find ![]()