1983 AHSME Problems/Problem 23
Problem
In the adjoining figure the five circles are tangent to one another consecutively and to the lines
![]() and
and ![]() .
If the radius of the largest circle is
.
If the radius of the largest circle is ![]() and that of the smallest one is
and that of the smallest one is ![]() , then the radius of the middle circle is
, then the radius of the middle circle is
![[asy] size(250);defaultpen(linewidth(0.7)); real alpha=5.797939254, x=71.191836; int i; for(i=0; i<5; i=i+1) { real r=8*(sqrt(6)/2)^i; draw(Circle((x+r)*dir(alpha), r)); x=x+2r; } real x=71.191836+40+20*sqrt(6), r=18; pair A=tangent(origin, (x+r)*dir(alpha), r, 1), B=tangent(origin, (x+r)*dir(alpha), r, 2); pair A1=300*dir(origin--A), B1=300*dir(origin--B); draw(B1--origin--A1); pair X=(69,-5), X1=reflect(origin, (x+r)*dir(alpha))*X, Y=(200,-5), Y1=reflect(origin, (x+r)*dir(alpha))*Y, Z=(130,0), Z1=reflect(origin, (x+r)*dir(alpha))*Z; clip(X--Y--Y1--X1--cycle); label("$L_2$", Z, S); label("$L_1$", Z1, dir(2*alpha)*dir(90));[/asy]](http://latex.artofproblemsolving.com/a/a/a/aaa7232e66c0c4c548469d800da4877f6661951f.png)
![]()
Solution
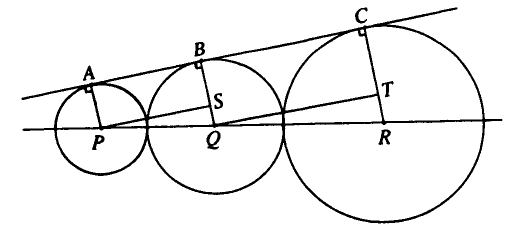
Consider three consecutive circles, as shown in the diagram above; observe that their centres ![]() ,
, ![]() , and
, and ![]() are collinear by symmetry. Let
are collinear by symmetry. Let ![]() ,
, ![]() , and
, and ![]() be the points of tangency, and let
be the points of tangency, and let ![]() and
and ![]() be segments parallel to the upper tangent (i.e.
be segments parallel to the upper tangent (i.e. ![]() ), as also shown. Since
), as also shown. Since ![]() is parallel to
is parallel to ![]() (the three points are collinear),
(the three points are collinear), ![]() is parallel to
is parallel to ![]() (as both are parallel to
(as both are parallel to ![]() ), and
), and ![]() is parallel to
is parallel to ![]() (as both are perpendicular to
(as both are perpendicular to ![]() , due to the tangent being perpendicular to the radius), we have
, due to the tangent being perpendicular to the radius), we have ![]() .
.
Now, if we let ![]() , and
, and ![]() be the radii of the three circles (from smallest to largest), then
be the radii of the three circles (from smallest to largest), then ![]() and
and ![]() . Thus, from the similarity that we just proved,
. Thus, from the similarity that we just proved, ![]() (where e.g.
(where e.g. ![]() because of collinearity). This equation reduces to
because of collinearity). This equation reduces to ![]() , i.e.
, i.e. ![]() , so the ratio of consecutive radii is constant, forming a geometric sequence. In this case, as the first radius is
, so the ratio of consecutive radii is constant, forming a geometric sequence. In this case, as the first radius is ![]() and, four radii later, the radius is
and, four radii later, the radius is ![]() , this constant ratio is
, this constant ratio is ![]() . Therefore the middle radius is
. Therefore the middle radius is ![$8 \cdot {\left(\sqrt[\leftroot{-2}\uproot{2}{4}]{\frac{18}{8}}\right)}^{2} = 8 \sqrt{\frac{18}{8}} = \sqrt{18 \cdot 8} = \sqrt{144} = 12$](http://latex.artofproblemsolving.com/d/b/4/db4fe516d7f2d9c8e27596f7d90bdabb6c6310b9.png) , which is choice
, which is choice ![]() .
.
See Also
| 1983 AHSME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 22 |
Followed by Problem 24 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 | ||
| All AHSME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()