2012 AMC 12B Problems/Problem 19
Contents
[hide]Problem
A unit cube has vertices ![]() and
and ![]() . Vertices
. Vertices ![]() ,
, ![]() , and
, and ![]() are adjacent to
are adjacent to ![]() , and for
, and for ![]() vertices
vertices ![]() and
and ![]() are opposite to each other. A regular octahedron has one vertex in each of the segments
are opposite to each other. A regular octahedron has one vertex in each of the segments ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . What is the octahedron's side length?
. What is the octahedron's side length?
![[asy] import three; size(7.5cm); triple eye = (-4, -8, 3); currentprojection = perspective(eye); triple[] P = {(1, -1, -1), (-1, -1, -1), (-1, 1, -1), (-1, -1, 1), (1, -1, -1)}; // P[0] = P[4] for convenience triple[] Pp = {-P[0], -P[1], -P[2], -P[3], -P[4]}; // draw octahedron triple pt(int k){ return (3*P[k] + P[1])/4; } triple ptp(int k){ return (3*Pp[k] + Pp[1])/4; } draw(pt(2)--pt(3)--pt(4)--cycle, gray(0.6)); draw(ptp(2)--pt(3)--ptp(4)--cycle, gray(0.6)); draw(ptp(2)--pt(4), gray(0.6)); draw(pt(2)--ptp(4), gray(0.6)); draw(pt(4)--ptp(3)--pt(2), gray(0.6) + linetype("4 4")); draw(ptp(4)--ptp(3)--ptp(2), gray(0.6) + linetype("4 4")); // draw cube for(int i = 0; i < 4; ++i){ draw(P[1]--P[i]); draw(Pp[1]--Pp[i]); for(int j = 0; j < 4; ++j){ if(i == 1 || j == 1 || i == j) continue; draw(P[i]--Pp[j]); draw(Pp[i]--P[j]); } dot(P[i]); dot(Pp[i]); dot(pt(i)); dot(ptp(i)); } label("$P_1$", P[1], dir(P[1])); label("$P_2$", P[2], dir(P[2])); label("$P_3$", P[3], dir(-45)); label("$P_4$", P[4], dir(P[4])); label("$P'_1$", Pp[1], dir(Pp[1])); label("$P'_2$", Pp[2], dir(Pp[2])); label("$P'_3$", Pp[3], dir(-100)); label("$P'_4$", Pp[4], dir(Pp[4])); [/asy]](http://latex.artofproblemsolving.com/5/9/d/59d2570727a6deab28e0d8d2be5154efc56b50ca.png)
![]()
Solution 1
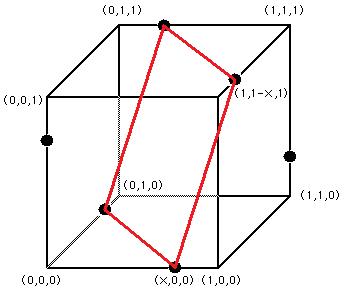
Observe the diagram above. Each dot represents one of the six vertices of the regular octahedron. Three dots have been placed exactly x units from the ![]() corner of the unit cube. The other three dots have been placed exactly x units from the
corner of the unit cube. The other three dots have been placed exactly x units from the ![]() corner of the unit cube. A red square has been drawn connecting four of the dots to provide perspective regarding the shape of the octahedron. Observe that the three dots that are near
corner of the unit cube. A red square has been drawn connecting four of the dots to provide perspective regarding the shape of the octahedron. Observe that the three dots that are near ![]() are each
are each ![]() ) from each other. The same is true for the three dots that are near
) from each other. The same is true for the three dots that are near ![]() There is a unique
There is a unique ![]() for which the rectangle drawn in red becomes a square. This will occur when the distance from
for which the rectangle drawn in red becomes a square. This will occur when the distance from ![]() to
to ![]() is
is ![]() ).
).
Using the distance formula we find the distance between the two points to be: ![]() =
= ![]() . Equating this to
. Equating this to ![]() ) and squaring both sides, we have the equation:
) and squaring both sides, we have the equation:
![]() =
= ![]()
![]()
![]() =
= ![]() .
.
Since the length of each side is ![]() ), we have a final result of
), we have a final result of ![]() . Thus, Answer choice
. Thus, Answer choice ![]() is correct.
is correct.
(If someone can draw a better diagram with the points labeled P1,P2, etc., I would appreciate it).
--Jm314 14:55, 26 February 2012 (EST)
Solution 2
Standard 3D geometry, no coordinates.
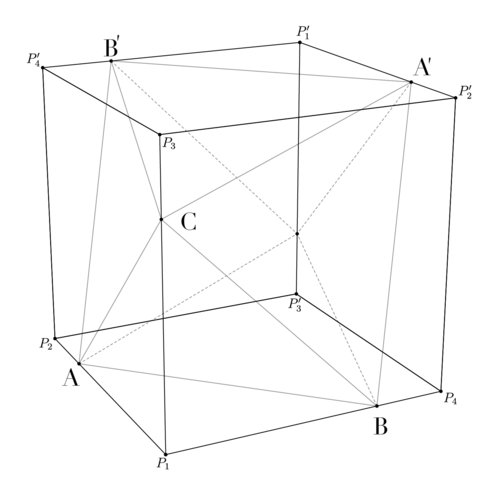
Let the tip of the octahedron on side ![]() be
be ![]() and the opposite vertex be
and the opposite vertex be ![]() . Our key is to examine the trapezoid
. Our key is to examine the trapezoid ![]() .
.
Let the side length of the octahedron be ![]() . Then
. Then ![]() and
and ![]() . Then, we have
. Then, we have ![]() . Finally, we want to find
. Finally, we want to find ![]() , which is just double the height of half the octahedron. We can use Pythagorean Theorem to find that height as
, which is just double the height of half the octahedron. We can use Pythagorean Theorem to find that height as ![]() . Now, we use the Pythagorean Theorem on the trapezoid. We get
. Now, we use the Pythagorean Theorem on the trapezoid. We get
![]()
![]()
~superagh
Solution 3
Let the length of ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
As ![]() ,
, ![]() ,
, ![]() ,
, ![]()

See Also
| 2012 AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 18 |
Followed by Problem 20 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()