2017 AIME I Problems/Problem 15
Contents
[hide]- 1 Problem 15
- 2 Solution 1
- 3 Solution 2
- 4 Solution 3
- 5 Solution 4 (Trigonometry)
- 6 Solution 5 (Complex numbers)
- 7 Solution 6
- 8 Solution 7
- 9 Solution 8
- 10 Solution 9 (Non Analytic)
- 11 Solution 10
- 12 Solution 11
- 13 Solution 12 (Geometry)
- 14 Solution 13 (Kinematics+Geometry)
- 15 Solution 13 (Fastest Trig)
- 16 See Also
Problem 15
The area of the smallest equilateral triangle with one vertex on each of the sides of the right triangle with side lengths ![]() and
and ![]() as shown, is
as shown, is ![]() where
where ![]() and
and ![]() are positive integers,
are positive integers, ![]() and
and ![]() are relatively prime, and
are relatively prime, and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]()
![[asy] size(5cm); pair C=(0,0),B=(0,2*sqrt(3)),A=(5,0); real t = .385, s = 3.5*t-1; pair R = A*t+B*(1-t), P=B*s; pair Q = dir(-60) * (R-P) + P; fill(P--Q--R--cycle,gray); draw(A--B--C--A^^P--Q--R--P); dot(A--B--C--P--Q--R); [/asy]](http://latex.artofproblemsolving.com/2/0/4/2040951aabf67ea7477c8aa658e56ccda3a56492.png)
Solution 1
Lemma: If ![]() satisfy
satisfy ![]() , then the minimal value of
, then the minimal value of ![]() is
is ![]() .
.
Proof: Recall that the distance between the point ![]() and the line
and the line ![]() is given by
is given by ![]() . In particular, the distance between the origin and any point
. In particular, the distance between the origin and any point ![]() on the line
on the line ![]() is at least
is at least ![]() .
.
---
Let the vertices of the right triangle be ![]() and let
and let ![]() be the two vertices of the equilateral triangle on the legs of the right triangle. Then, the third vertex of the equilateral triangle is
be the two vertices of the equilateral triangle on the legs of the right triangle. Then, the third vertex of the equilateral triangle is  . This point must lie on the hypotenuse
. This point must lie on the hypotenuse ![]() , i.e.
, i.e. ![]() must satisfy
must satisfy
![]() which can be simplified to
which can be simplified to
![]()
By the lemma, the minimal value of ![]() is
is
![\[\frac{1}{\sqrt{\left(\frac{7}{20}\right)^2 + \left(\frac{11\sqrt{3}}{60}\right)^2}} = \frac{10\sqrt{3}}{\sqrt{67}},\]](http://latex.artofproblemsolving.com/9/4/d/94dba6f485bdf86325dcb8d0fd0562ff38adff02.png) so the minimal area of the equilateral triangle is
so the minimal area of the equilateral triangle is
![\[\frac{\sqrt{3}}{4} \cdot \left(\frac{10\sqrt{3}}{\sqrt{67}}\right)^2 = \frac{\sqrt{3}}{4} \cdot \frac{300}{67} = \frac{75\sqrt{3}}{67},\]](http://latex.artofproblemsolving.com/f/a/2/fa2164930d825d52eda5643945d73784f51576ea.png) and hence the answer is
and hence the answer is ![]() .
.
Solution 2
Let ![]() ,
, ![]() lies on
lies on ![]() ,
, ![]() lies on
lies on ![]() and
and ![]() lies on
lies on ![]()
Set ![]() as the origin,
as the origin, ![]() ,
, ![]() can be expressed as
can be expressed as ![]() in argand plane, the distance of
in argand plane, the distance of ![]() is
is ![]()
We know that ![]() . We know that the slope of
. We know that the slope of ![]() is
is ![]() , we have that
, we have that  , after computation, we have
, after computation, we have ![]()
Now the rest is easy with C-S inequality, ![]() so the smallest area is
so the smallest area is ![]() , and the answer is
, and the answer is ![]()
~bluesoul
Solution 3
Let ![]() be the right triangle with sides
be the right triangle with sides ![]() ,
, ![]() , and
, and ![]() and right angle at
and right angle at ![]() .
.
Let an equilateral triangle touch ![]() ,
, ![]() , and
, and ![]() at
at ![]() ,
, ![]() , and
, and ![]() respectively, having side lengths of
respectively, having side lengths of ![]() .
.
Now, call ![]() as
as ![]() and
and ![]() as
as ![]() . Thus,
. Thus, ![]() and
and ![]() .
.
By Law of Sines on triangles ![]() and
and ![]() ,
,
![]() and
and ![]() .
.
Summing,
![]() .
.
Now substituting ![]() ,
, ![]() , and
, and ![]() and solving,
and solving,
![]() .
.
We seek to minimize ![]() .
.
This is equivalent to minimizing ![]() .
.
Using the lemma from solution 1, we conclude that ![]()
Thus, ![]() and our final answer is
and our final answer is ![]()
- Awsomness2000
Solution 4 (Trigonometry)
Let ![]()
Then ![]()
![]()
By Law of Sines on triangle ![]() we get
we get
![]()
![]()
![]()
![]()
![]()
![\[\frac{AC}{x} \le \sqrt {\left(\cot \alpha + \frac {\sqrt3}{2}\right)^2 + \left(\frac {1}{2}\right)^2} = \sqrt {\cot^2 \alpha + \sqrt {3} \cot \alpha + 1}\]](http://latex.artofproblemsolving.com/c/3/1/c31638468dabc20b97006d3a1ab89205bb61ac36.png) The smallest area
The smallest area ![]() is
is
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Note
![]() follows from Cauchy-Schwarz.
follows from Cauchy-Schwarz.
![]() ~mathboy282
~mathboy282
Solution 5 (Complex numbers)
We will use complex numbers. Set the vertex at the right angle to be the origin, and set the axes so the other two vertices are ![]() and
and ![]() , respectively. Now let the vertex of the equilateral triangle on the real axis be
, respectively. Now let the vertex of the equilateral triangle on the real axis be ![]() and let the vertex of the equilateral triangle on the imaginary axis be
and let the vertex of the equilateral triangle on the imaginary axis be ![]() . Then, the third vertex of the equilateral triangle is given by:
. Then, the third vertex of the equilateral triangle is given by:
![]() .
.
For this to be on the hypotenuse of the right triangle, we also have the following:
![\[\frac{\frac{a\sqrt{3}}{2}+\frac{1}{2}}{\frac{a}{2}+\frac{b\sqrt{3}}{2}-5}=-\frac{2\sqrt{3}}{5}\iff 7\sqrt{3}a+11b=20\sqrt{3}\]](http://latex.artofproblemsolving.com/b/9/8/b989f24f27bf88a37a1fa4d8b41fb770fa9f4a47.png)
Note that the area of the equilateral triangle is given by ![]() , so we seek to minimize
, so we seek to minimize ![]() . This can be done by using the Cauchy Schwarz Inequality on the relation we derived above:
. This can be done by using the Cauchy Schwarz Inequality on the relation we derived above:
![]()
Thus, the minimum we seek is simply ![]() , so the desired answer is
, so the desired answer is ![]() .
.
Solution 6
In the complex plane, let the vertices of the triangle be ![]()
![]() and
and ![]() Let
Let ![]() be one of the vertices, where
be one of the vertices, where ![]() is real. A point on the line passing through
is real. A point on the line passing through ![]() and
and ![]() can be expressed in the form
can be expressed in the form
![]() We want the third vertex
We want the third vertex ![]() to lie on the line through
to lie on the line through ![]() and
and ![]() which is the imaginary axis, so its real part is 0.
Since the small triangle is equilateral,
which is the imaginary axis, so its real part is 0.
Since the small triangle is equilateral, ![]() or
or
![]() Then the real part of
Then the real part of ![]() is
is
![]() Solving for
Solving for ![]() in terms of
in terms of ![]() we find
we find
![]() Then
Then
![]() so
so
![]() so
so
 This quadratic is minimized when
This quadratic is minimized when ![]() and the minimum is
and the minimum is ![]() so the smallest area of the equilateral triangle is
so the smallest area of the equilateral triangle is
![\[\frac{\sqrt{3}}{4} \cdot \frac{300}{67} = \boxed{\frac{75 \sqrt{3}}{67}}.\]](http://latex.artofproblemsolving.com/d/8/a/d8af728ad51851aba3c843fe958eff1c62019708.png)
Solution 7
We can use complex numbers. Set the origin at the right angle. Let the point on the real axis be ![]() and the point on the imaginary axis be
and the point on the imaginary axis be ![]() . Then, we see that
. Then, we see that  Now we switch back to Cartesian coordinates. The equation of the hypotenuse is
Now we switch back to Cartesian coordinates. The equation of the hypotenuse is ![]() This means that the point
This means that the point  is on the line. Plugging the numbers in, we have
is on the line. Plugging the numbers in, we have ![]() Now, we note that the side length of the equilateral triangle is
Now, we note that the side length of the equilateral triangle is ![]() so it suffices to minimize that. By Cauchy-Schwarz, we have
so it suffices to minimize that. By Cauchy-Schwarz, we have ![]() Thus, the area of the smallest triangle is
Thus, the area of the smallest triangle is ![]() so our desired answer is
so our desired answer is ![]() .
.
(Solution by Pleaseletmetwin, but not added to the Wiki by Pleaseletmetwin)
Solution 8
Employ the same complex bash as in Solution 5, but instead note that minimizing ![]() is the same as minimizing the distance from
0,0 to x,y, since they are the same quantity. We use point to plane instead, which gives you the required distance.
is the same as minimizing the distance from
0,0 to x,y, since they are the same quantity. We use point to plane instead, which gives you the required distance.
Solution 9 (Non Analytic)
Let ![]() be the triangle with side lengths
be the triangle with side lengths ![]() and
and ![]() .
.
We will think about this problem backwards, by constructing a triangle as large as possible (We will call it ![]() , for convenience) which is similar to
, for convenience) which is similar to ![]() with vertices outside of a unit equilateral triangle
with vertices outside of a unit equilateral triangle ![]() , such that each vertex of the equilateral triangle lies on a side of
, such that each vertex of the equilateral triangle lies on a side of ![]() . After we find the side lengths of
. After we find the side lengths of ![]() , we will use ratios to trace back towards the original problem.
, we will use ratios to trace back towards the original problem.
First of all, let ![]() ,
,  , and
, and ![]() (These three angles are simply the angles of triangle
(These three angles are simply the angles of triangle ![]() ; out of these three angles,
; out of these three angles, ![]() is the smallest angle, and
is the smallest angle, and ![]() is the largest angle). Then let us consider a point
is the largest angle). Then let us consider a point ![]() inside
inside ![]() such that
such that ![]() ,
, ![]() , and
, and ![]() . Construct the circumcircles
. Construct the circumcircles ![]() and
and ![]() of triangles
of triangles ![]() and
and ![]() respectively.
respectively.
From here, we will prove the lemma that if we choose points ![]() ,
, ![]() , and
, and ![]() on circumcircles
on circumcircles ![]() and
and ![]() respectively such that
respectively such that ![]() ,
, ![]() , and
, and ![]() are collinear and
are collinear and ![]() ,
, ![]() , and
, and ![]() are collinear, then
are collinear, then ![]() ,
, ![]() , and
, and ![]() must be collinear. First of all, if we let
must be collinear. First of all, if we let ![]() , then
, then ![]() (by the properties of cyclic quadrilaterals),
(by the properties of cyclic quadrilaterals), ![]() (by adjacent angles),
(by adjacent angles), ![]() (by cyclic quadrilaterals),
(by cyclic quadrilaterals), ![]() (adjacent angles), and
(adjacent angles), and ![]() (cyclic quadrilaterals). Since
(cyclic quadrilaterals). Since ![]() and
and ![]() are supplementary,
are supplementary, ![]() ,
, ![]() , and
, and ![]() are collinear as desired. Hence,
are collinear as desired. Hence, ![]() has an inscribed equilateral triangle
has an inscribed equilateral triangle ![]() .
.
In addition, now we know that all triangles ![]() (as described above) must be similar to triangle
(as described above) must be similar to triangle ![]() , as
, as ![]() and
and ![]() , so we have developed
, so we have developed ![]() similarity between the two triangles. Thus,
similarity between the two triangles. Thus, ![]() is the triangle similar to
is the triangle similar to ![]() which we were desiring. Our goal now is to maximize the length of
which we were desiring. Our goal now is to maximize the length of ![]() , in order to maximize the area of
, in order to maximize the area of ![]() , to achieve our original goal.
, to achieve our original goal.
Note that, all triangles ![]() are similar to each other if
are similar to each other if ![]() ,
, ![]() , and
, and ![]() are collinear. This is because
are collinear. This is because ![]() is constant, and
is constant, and ![]() is also a constant value. Then we have
is also a constant value. Then we have ![]() similarity between this set of triangles. To maximize
similarity between this set of triangles. To maximize ![]() , we can instead maximize
, we can instead maximize ![]() , which is simply the diameter of
, which is simply the diameter of ![]() . From there, we can determine that
. From there, we can determine that ![]() , and with similar logic,
, and with similar logic, ![]() ,
, ![]() , and
, and ![]() are perpendicular to
are perpendicular to ![]() ,
, ![]() , and
, and ![]() respectively We have found our desired largest possible triangle
respectively We have found our desired largest possible triangle ![]() .
.
All we have to do now is to calculate ![]() , and use ratios from similar triangles to determine the side length of the equilateral triangle inscribed within
, and use ratios from similar triangles to determine the side length of the equilateral triangle inscribed within ![]() . First of all, we will prove that
. First of all, we will prove that ![]() . By the properties of cyclic quadrilaterals,
. By the properties of cyclic quadrilaterals, ![]() , which means that
, which means that ![]() . Now we will show that
. Now we will show that ![]() . Note that, by cyclic quadrilaterals,
. Note that, by cyclic quadrilaterals, ![]() and
and ![]() . Hence,
. Hence, ![]() (since
(since ![]() ), proving the aforementioned claim. Then, since
), proving the aforementioned claim. Then, since ![]() and
and ![]() ,
, ![]() .
.
Now we calculate ![]() and
and ![]() , which are simply the diameters of circumcircles
, which are simply the diameters of circumcircles ![]() and
and ![]() , respectively. By the extended law of sines,
, respectively. By the extended law of sines, ![]() and
and ![]() .
.
We can now solve for ![]() with the law of cosines:
with the law of cosines:
![\[(ZY)^2 = \frac{37}{25} + \frac{37}{12} - \left(\frac{37}{5\sqrt{3}}\right)\left(-\frac{\sqrt{3}}{2}\right)\]](http://latex.artofproblemsolving.com/3/9/2/3928918d3a3fde7254bf342cbfbea4bfae557f3c.png)
![]()
![]()
![]()
Now we will apply this discovery towards our original triangle ![]() . Since the ratio between
. Since the ratio between ![]() and the hypotenuse of
and the hypotenuse of ![]() is
is ![]() , the side length of the equilateral triangle inscribed within
, the side length of the equilateral triangle inscribed within ![]() must be
must be ![]() (as
(as ![]() is simply as scaled version of
is simply as scaled version of ![]() , and thus their corresponding inscribed equilateral triangles must be scaled by the same factor). Then the area of the equilateral triangle inscribed within
, and thus their corresponding inscribed equilateral triangles must be scaled by the same factor). Then the area of the equilateral triangle inscribed within ![]() is
is ![]() , implying that the answer is
, implying that the answer is ![]() .
.
-Solution by TheBoomBox77
Solution 10
Let the right triangle's lower-left point be at ![]() . Notice the 2 other points will determine a unique equilateral triangle. Let 2 points be on the
. Notice the 2 other points will determine a unique equilateral triangle. Let 2 points be on the ![]() -axis (
-axis (![]() ) and the
) and the ![]() -axis (
-axis (![]() ) and label them
) and label them ![]() and
and ![]() respectively. The third point (
respectively. The third point (![]() ) will then be located on the hypotenuse. We proceed to find the third point's coordinates in terms of
) will then be located on the hypotenuse. We proceed to find the third point's coordinates in terms of ![]() and
and ![]() .
.
1. Find the slope of ![]() and take the negative reciprocal of it to find the slope of the line containing
and take the negative reciprocal of it to find the slope of the line containing ![]() . Notice the line contains the midpoint of
. Notice the line contains the midpoint of ![]() so we can then have an equation of the line.
so we can then have an equation of the line.
2. Let ![]() For
For ![]() to be an equilateral triangle, the altitude from
to be an equilateral triangle, the altitude from ![]() to
to ![]() must be
must be ![]()
We then have two equations and two variables, so we can solve for ![]() 's coordinates.
's coordinates.
We can find ![]() Also, note that
Also, note that ![]() must be on the hypotenuse of the triangle
must be on the hypotenuse of the triangle ![]() We can plug in
We can plug in ![]() and
and ![]() as the coordinates of
as the coordinates of ![]() , which simplifies to
, which simplifies to
![]()
We aim to minimize the side length of the triangle, which is ![]() Applying the Cauchy inequality gives us
Applying the Cauchy inequality gives us
![]()
From which we obtain ![]() Thus, the area of the triangle =
Thus, the area of the triangle = ![]() which leads to the answer
which leads to the answer ![]()
-hi_im_bob
Solution 11
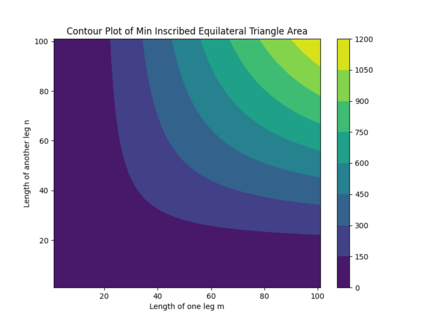
The general solution to the minimal area is as following:
![]()
where ![]() and
and ![]() are the two legs of the right triangle. In this particular case
are the two legs of the right triangle. In this particular case ![]() and
and ![]() . When we plug in these two values, we recover the correct answer of
. When we plug in these two values, we recover the correct answer of ![]() .
.
The contour of the minimal area ![]() is plotted as a function of leg lengths
is plotted as a function of leg lengths ![]() and
and ![]() , as shown on the right hand side.
, as shown on the right hand side.
Note
The proof of the formula can be done in a similar fashion as Solution 4, where instead of using specific values, we define variables, ![]() and
and ![]() in this case, as per the formula.
in this case, as per the formula.
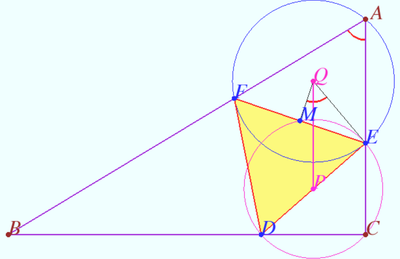
Solution 12 (Geometry)
Let ![]() Then
Then ![]()
![]() midpoint
midpoint ![]() midpoint
midpoint ![]() circumcenter
circumcenter ![]()
![]()
![]()
![]()
![]()
![]() Points
Points ![]() and
and ![]() lies on bisectors of
lies on bisectors of ![]() and
and ![]() so
so ![]()
The smallest area ![]() is
is
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
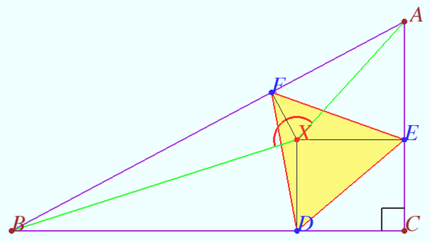
Solution 13 (Kinematics+Geometry)
Let ![]() Then
Then ![]()
Let the required triangle with minimal sides ![]() be constructed.
be constructed.
Let us vary its position in an acceptable way, that is, we will perform a movement in which the vertices of the ![]() remain on the sides of the
remain on the sides of the ![]() Any motion of a solid plane figure can be considered as rotation around some point, the center of rotation. The speed of movement of any point is perpendicular to the segment from the center of rotation to this point. With an acceptable variation, the velocities of the vertices of the
Any motion of a solid plane figure can be considered as rotation around some point, the center of rotation. The speed of movement of any point is perpendicular to the segment from the center of rotation to this point. With an acceptable variation, the velocities of the vertices of the ![]() are directed along the sides
are directed along the sides ![]() Consequently, there is a point
Consequently, there is a point ![]() located at the intersection of perpendiculars to the sides of
located at the intersection of perpendiculars to the sides of ![]() around which
around which ![]() rotates. The bases of the perpendiculars dropped from
rotates. The bases of the perpendiculars dropped from ![]() to the sides of
to the sides of ![]() form a regular
form a regular ![]()
Therefore ![]() is the first isodynamic point of
is the first isodynamic point of ![]()
It is known that ![]()
The points ![]() and
and ![]() are concyclic,
are concyclic, ![]() is the diameter, so
is the diameter, so ![]() Similarly,
Similarly, ![]()
![]()
![]() The smallest area
The smallest area ![]() is
is
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Solution 13 (Fastest Trig)
Let the right triangle be ![]() with
with ![]() ,
, ![]() , and
, and ![]() , and let the equilateral be
, and let the equilateral be ![]() with
with ![]() on
on ![]() respectively. Call its side length
respectively. Call its side length ![]() . Let the foot from
. Let the foot from ![]() to
to ![]() be
be ![]() , and let
, and let ![]() . Since
. Since ![]() ,
, ![]() . We get
. We get ![]() and
and ![]() . Meanwhile, since
. Meanwhile, since ![]() and
and ![]() ,
, ![]() . We have
. We have
![]()
![\[\implies 2\sqrt{3}=x\left(\frac{2\sqrt{3}}{5}\sin\theta+\cos\theta-\frac{1}{2}\cos\theta+\frac{\sqrt{3}}{2}\sin\theta\right)\]](http://latex.artofproblemsolving.com/5/9/c/59c12319a3d7f200f53c2f5d8b5a6f9f35723be1.png)
![\[\implies x=\frac{2\sqrt{3}}{\frac{9\sqrt{3}}{10}\sin\theta+\frac{1}{2}\cos\theta}.\]](http://latex.artofproblemsolving.com/e/b/8/eb88ce0e2f1618c883104cfc8dffb9cc1f85809f.png)
![\[\implies [\triangle DEF]=\frac{\sqrt{3}}{4}x^2=\frac{\sqrt{3}}{4}\cdot \frac{12}{\left(\frac{9\sqrt{3}}{10}\sin\theta+\frac{1}{2}\cos\theta\right)^2}=\frac{3\sqrt{3}}{\left(\frac{9\sqrt{3}}{10}\sin\theta+\frac{1}{2}\cos\theta \right)^2}\]](http://latex.artofproblemsolving.com/f/5/6/f561338927cfef9a7a7fd4751719601d7710ac25.png)
By Cauchy-Schwarz, ![\[\left(\frac{9\sqrt{3}}{10}\sin\theta+\frac{1}{2}\cos\theta \right)^2 \le \left(\cos^2\theta+\sin^2\theta\right)\left(\left(\frac{9\sqrt{3}}{10}\right)^2+\left(\frac{1}{2}\right)^2\right)=\frac{67}{25}\]](http://latex.artofproblemsolving.com/3/1/8/3188d6c48f4de97c169003bd1c305a761c9790e8.png)
![]()
The requested sum is ![]() .
.
~bomberdoodles
See Also
| 2017 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Problem | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()