2018 AIME II Problems/Problem 12
Contents
[hide]- 1 Problem
- 2 Diagram
- 3 Solution 1
- 4 Solution 2
- 5 Solution 3 (Another way to get the middle point)
- 6 Solution 4 (With yet another way to get the middle point)
- 7 Solution 5
- 8 Solution 6
- 9 Solution 7
- 10 Solution 8 (Simple Geometry)
- 11 Solution 9 (Mindless Law of Cosines Bash)
- 12 Solution 10
- 13 Solution 11
- 14 Video Solution by MOP 2024
- 15 See Also
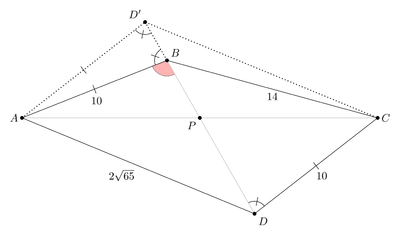
Problem
Let ![]() be a convex quadrilateral with
be a convex quadrilateral with ![]() ,
, ![]() , and
, and ![]() . Assume that the diagonals of
. Assume that the diagonals of ![]() intersect at point
intersect at point ![]() , and that the sum of the areas of triangles
, and that the sum of the areas of triangles ![]() and
and ![]() equals the sum of the areas of triangles
equals the sum of the areas of triangles ![]() and
and ![]() . Find the area of quadrilateral
. Find the area of quadrilateral ![]() .
.
Diagram
Let ![]() and let
and let ![]() . Let
. Let ![]() and let
and let ![]() .
.
![[asy] defaultpen(fontsize(14)+0.6); unitsize(12); real x=11.25; pair B1=origin, D1=(x,0), C1=IP(CR(B1,14),CR(D1,10)), A1=OP(CR(B1,10),CR(D1,2*sqrt(65))), P1=extension(A1,C1,B1,D1); pair A=origin, C=(length(C1-A1),0), B=IP(CR(A,10),CR(C,14)), D=OP(CR(A,2*sqrt(65)),CR(C,10)), P=extension(A,C,B,D); draw(A--B--C--D--A); draw(A--C^^B--D,gray+0.4); dot("$A$",A,dir(A-P)); dot("$B$",B,dir(B-P)); dot("$C$",C,dir(C-P)); dot("$D$",D,dir(D-P)); dot("$P$",P,dir(230)); pen p=fontsize(10); label("$10$",A--B,up,p); label("$10$", C--D, 2*right,p); label("$14$", B--C, N,p); label("$2\sqrt{65}$", A--D, SW,p); label("$x$", A--P,down,p); label("$\rho x$", P--C,down,p); label("$\Delta$",(A+B+P)/3, right,p); label("$\Lambda$",(A+D+P)/3, right,p); [/asy]](http://latex.artofproblemsolving.com/5/b/9/5b92b18d1f112303661bb41729dfe62f508b4dd1.png)
Solution 1
Let ![]() and let
and let ![]() . Let
. Let ![]() and let
and let ![]() . We easily get
. We easily get ![]() and
and ![]() .
.
We are given that ![]() , which we can now write as
, which we can now write as ![]() Either
Either ![]() or
or ![]() . The former would imply that
. The former would imply that ![]() is a parallelogram, which it isn't; therefore we conclude
is a parallelogram, which it isn't; therefore we conclude ![]() and
and ![]() is the midpoint of
is the midpoint of ![]() . Let
. Let ![]() and
and ![]() . Then
. Then ![]() . On one hand, since
. On one hand, since ![]() , we have
, we have ![]() whereas, on the other hand, using cosine formula to get the length of
whereas, on the other hand, using cosine formula to get the length of ![]() , we get
, we get ![]()
![]() Eliminating
Eliminating ![]() in the above two equations and solving for
in the above two equations and solving for ![]() we get
we get![]() which finally yields
which finally yields ![]() .
.
Solution 2
For reference, ![]() , so
, so ![]() is the longest of the four sides of
is the longest of the four sides of ![]() . Let
. Let ![]() be the length of the altitude from
be the length of the altitude from ![]() to
to ![]() , and let
, and let ![]() be the length of the altitude from
be the length of the altitude from ![]() to
to ![]() . Then, the triangle area equation becomes
. Then, the triangle area equation becomes
![]()
What an important finding! Note that the opposite sides ![]() and
and ![]() have equal length, and note that diagonal
have equal length, and note that diagonal ![]() bisects diagonal
bisects diagonal ![]() . This is very similar to what happens if
. This is very similar to what happens if ![]() were a parallelogram with
were a parallelogram with ![]() , so let's extend
, so let's extend ![]() to point
to point ![]() , such that
, such that ![]() is a parallelogram. In other words,
is a parallelogram. In other words, ![]() and
and ![]() Now, let's examine
Now, let's examine ![]() . Since
. Since ![]() , the triangle is isosceles, and
, the triangle is isosceles, and ![]() . Note that in parallelogram
. Note that in parallelogram ![]() ,
, ![]() and
and ![]() are congruent, so
are congruent, so ![]() and thus
and thus ![]() Define
Define ![]() , so
, so ![]() .
.
We use the Law of Cosines on ![]() and
and ![]() :
:
![]()
![]()
Subtracting the second equation from the first yields
![]()
This means that dropping an altitude from ![]() to some foot
to some foot ![]() on
on ![]() gives
gives ![]() and therefore
and therefore ![]() . Seeing that
. Seeing that ![]() , we conclude that
, we conclude that ![]() is a 3-4-5 right triangle, so
is a 3-4-5 right triangle, so ![]() . Then, the area of
. Then, the area of ![]() is
is ![]() . Since
. Since ![]() , points
, points ![]() and
and ![]() are equidistant from
are equidistant from ![]() , so
, so ![]() and hence
and hence ![]() -kgator
-kgator
Just to be complete -- ![]() and
and ![]() can actually be equal. In this case,
can actually be equal. In this case, ![]() , but
, but ![]() must be equal to
must be equal to ![]() . We get the same result. -Mathdummy.
. We get the same result. -Mathdummy.
Solution 3 (Another way to get the middle point)
So, let the area of ![]() triangles
triangles ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Suppose
. Suppose ![]() and
and ![]() , then it is easy to show that
, then it is easy to show that ![]() Also, because
Also, because ![]() we will have
we will have ![]() So
So ![]() So
So ![]() So
So ![]() So
So ![]() As a result,
As a result, ![]() Then, we have
Then, we have ![]() Combine the condition
Combine the condition ![]() we can find out that
we can find out that ![]() so
so ![]() is the midpoint of
is the midpoint of ![]()
~Solution by ![]() (Frank FYC)
(Frank FYC)
Solution 4 (With yet another way to get the middle point)
Denote ![]() by
by ![]() . Then
. Then ![]() .
Using the formula for the area of a triangle, we get
.
Using the formula for the area of a triangle, we get ![]() so
so ![]() Hence
Hence ![]() (note that
(note that ![]() makes no difference here).
Now, assume that
makes no difference here).
Now, assume that ![]() ,
, ![]() , and
, and ![]() . Using the cosine rule for
. Using the cosine rule for ![]() and
and ![]() , it is clear that
, it is clear that ![]() or
or  Likewise, using the cosine rule for triangles
Likewise, using the cosine rule for triangles ![]() and
and ![]() ,
,  It follows that
It follows that  Since
Since ![]() ,
, ![\[\sqrt{1-\frac{(x^2+y^2-100)^2}{4x^2y^2}}=\sqrt{1-\frac{(x^2+z^2-260)^2}{4x^2z^2}}\]](http://latex.artofproblemsolving.com/5/9/e/59eac63e2d72cd0e55c09cc694ec22cac226b258.png) which simplifies to
which simplifies to ![]() Plugging this back to equations
Plugging this back to equations ![]() ,
, ![]() , and
, and ![]() , it can be solved that
, it can be solved that ![]() . Then, the area of the quadrilateral is
. Then, the area of the quadrilateral is ![]() --Solution by MicGu
--Solution by MicGu
Solution 5
As in all other solutions, we can first find that either ![]() or
or ![]() , but it's an AIME problem, we can take
, but it's an AIME problem, we can take ![]() , and assume the other choice will lead to the same result (which is true).
, and assume the other choice will lead to the same result (which is true).
From ![]() , we have
, we have ![]() , and
, and ![]() , therefore,
, therefore,
 By Law of Cosines,
By Law of Cosines,
 Square
Square ![]() and
and ![]() , and add them, to get
, and add them, to get
![]() Solve,
Solve, ![]() ,
,
![]() -Mathdummy
-Mathdummy
Solution 6
Either ![]() or
or ![]() . Let
. Let ![]() . Applying Stewart's Theorem on
. Applying Stewart's Theorem on ![]() and
and ![]() , dividing by
, dividing by ![]() and rearranging,
and rearranging, ![]()
![]() Applying Stewart on
Applying Stewart on ![]() and
and ![]() ,
, ![]() Substituting equations 1 and 2 into 3 and rearranging,
Substituting equations 1 and 2 into 3 and rearranging, ![]() . By Law of Cosines on
. By Law of Cosines on ![]() ,
, ![]() so
so ![]() . Using
. Using ![]() to find unknown areas,
to find unknown areas, ![]() .
.
-Solution by Garrett
Solution 7
Now we prove P is the midpoint of ![]() . Denote the height from
. Denote the height from ![]() to
to ![]() as
as ![]() , height from
, height from ![]() to
to ![]() as
as ![]() .According to the problem,
.According to the problem, ![]() implies
implies ![]() . Then according to basic congruent triangles we get
. Then according to basic congruent triangles we get ![]() Firstly, denote that
Firstly, denote that ![]() . Applying Stewart theorem, getting that
. Applying Stewart theorem, getting that ![]() , denote
, denote ![]() Applying Stewart Theorem, getting
Applying Stewart Theorem, getting ![]() solve for a, getting
solve for a, getting ![]() Now everything is clear, we can find
Now everything is clear, we can find ![]() using LOC,
using LOC, ![]() , the whole area is
, the whole area is ![]()
~bluesoul
Solution 8 (Simple Geometry)
![]() as in another solutions.
as in another solutions.
Let ![]() be the reflection of
be the reflection of ![]() across
across ![]() .
Let points
.
Let points ![]() and
and ![]() be the foot of perpendiculars on
be the foot of perpendiculars on ![]() from
from ![]() , and
, and ![]() respectively.
respectively.
 The area of quadrilateral
The area of quadrilateral ![]() is equal to the area of triangle
is equal to the area of triangle ![]() with sides
with sides ![]() .
The semiperimeter is
.
The semiperimeter is ![]() the area
the area ![]()
vladimir.shelomovskii@gmail.com, vvsss
Solution 9 (Mindless Law of Cosines Bash)
Use your favorite method to get that ![]() is the midpoint of one of the two diagonals (suppose it's the midpoint of
is the midpoint of one of the two diagonals (suppose it's the midpoint of ![]() ). From here, let
). From here, let ![]() where
where ![]() is the angle that the diagonals make. Then we have a system of four equations:
is the angle that the diagonals make. Then we have a system of four equations:

From these equations we get that

From here we can see that ![]() so
so ![]() Furthermore, this implies
Furthermore, this implies ![]() and
and ![]() which implies
which implies ![]() Then note that the area of the quadrilateral is
Then note that the area of the quadrilateral is ![]()
~Dhillonr25
Solution 10
Note that ![]() (All angles are in degrees)
Since
(All angles are in degrees)
Since ![]() we can use sine area formula to get the following(after some simplifying steps):
we can use sine area formula to get the following(after some simplifying steps):
![]() For convenience, let
For convenience, let ![]() The above equation simplifies to:
The above equation simplifies to:
 From here, we see that
From here, we see that ![]() or
or ![]() . Without loss of generality, let
. Without loss of generality, let ![]() . Since triangles
. Since triangles ![]() and
and ![]() are obviously not congruent, we see that one triangle is obtuse and the other one is acute.(Refer to the diagram) However, if we drop perpendiculars from
are obviously not congruent, we see that one triangle is obtuse and the other one is acute.(Refer to the diagram) However, if we drop perpendiculars from ![]() to
to ![]() and
and ![]() to
to ![]() , we do get congruent triangles. If the foot of the perpendicular from
, we do get congruent triangles. If the foot of the perpendicular from ![]() is
is ![]() , and the foot of the perpendicular from
, and the foot of the perpendicular from ![]() is
is ![]() , then right triangle
, then right triangle ![]() is congruent to right triangle
is congruent to right triangle ![]() .
From here, we see that the altitudes of triangles
.
From here, we see that the altitudes of triangles ![]() and
and ![]() to
to ![]() are equal. Since they share base
are equal. Since they share base ![]() , their areas are equal. We can use Heron's formula. To not have any fractions, let
, their areas are equal. We can use Heron's formula. To not have any fractions, let ![]()
![]() Even though this looks bad at first, it actually isn't too complicated to simplify. Expanding the differences of squares and simplifying completely, we get
Even though this looks bad at first, it actually isn't too complicated to simplify. Expanding the differences of squares and simplifying completely, we get ![]() Plugging this
Plugging this ![]() back into the Heron's formula, we get that the area of
back into the Heron's formula, we get that the area of ![]() (or
(or ![]() ) is
) is ![]() . Since these triangles have equal area, the area of the quadrilateral is
. Since these triangles have equal area, the area of the quadrilateral is ![]() , and we are done.
, and we are done. ![]()
~ewei12
Solution 11
Use any method to derive that ![]() is the midpoint of
is the midpoint of ![]() and
and ![]() . Now, either construct a parallelogram with as shown in the diagram to the right, or use law of sines. We will take the parallelogram route here, but the same thing can be done with law of sines on triangles
. Now, either construct a parallelogram with as shown in the diagram to the right, or use law of sines. We will take the parallelogram route here, but the same thing can be done with law of sines on triangles ![]() and
and ![]() . Reflect
. Reflect ![]() across
across ![]() to get
to get ![]() . Since
. Since ![]() ,
, ![]() is isosceles. Thus,
is isosceles. Thus, ![]() , and because
, and because ![]() is a parallelogram (since
is a parallelogram (since ![]() and
and ![]() ),
), ![]() . So,
. So, ![]() . Now, apply law of cosines on
. Now, apply law of cosines on ![]() and
and ![]() . We get:
. We get:
![]() again, we obtain
again, we obtain
![]() Since
Since ![]() ,
, ![]() . Thus,
. Thus, ![]() .
.
Video Solution by MOP 2024
https://youtube.com/watch?v=2BsYR1dJn9c
~r00tsOfUnity
See Also
| 2018 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 11 |
Followed by Problem 13 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()