2019 AIME II Problems/Problem 5
Contents
[hide]Problem
Four ambassadors and one advisor for each of them are to be seated at a round table with ![]() chairs numbered in order
chairs numbered in order ![]() to
to ![]() . Each ambassador must sit in an even-numbered chair. Each advisor must sit in a chair adjacent to his or her ambassador. There are
. Each ambassador must sit in an even-numbered chair. Each advisor must sit in a chair adjacent to his or her ambassador. There are ![]() ways for the
ways for the ![]() people to be seated at the table under these conditions. Find the remainder when
people to be seated at the table under these conditions. Find the remainder when ![]() is divided by
is divided by ![]() .
.
Solution 0
Suppose first that the chairs weren't numbered, and rotation doesn't matter. Then if we let the ambassador-advisor pairs act as a single person, we essentially want to pick ![]() seats out of
seats out of ![]() seats, and fixing one pair gives
seats, and fixing one pair gives ![]() ways. However, now we want to number the seats, in which there are
ways. However, now we want to number the seats, in which there are ![]() possibilities (for some pair of people, we choose the order and then we choose which even spot the ambassador sits in, giving
possibilities (for some pair of people, we choose the order and then we choose which even spot the ambassador sits in, giving ![]() ) However, the order of the other pairs is then uniquely determined, so this method works, giving us
) However, the order of the other pairs is then uniquely determined, so this method works, giving us ![]() ways. We are asked to find the remainder when
ways. We are asked to find the remainder when ![]() is divided by
is divided by ![]() , which is
, which is ![]() .
~Maximilian113
~Minor edits by Hiphopfrog1
.
~Maximilian113
~Minor edits by Hiphopfrog1
Solution 1
Let us first consider the ![]() ambassadors and the
ambassadors and the ![]() even-numbered chairs. If we consider only their relative positions, they can sit in one of
even-numbered chairs. If we consider only their relative positions, they can sit in one of ![]() distinct ways: Such that the
distinct ways: Such that the ![]() empty even-numbered chairs are adjacent, such that they are separated by one occupied even-numbered chair, and such that they are opposite each other. For each way, there are
empty even-numbered chairs are adjacent, such that they are separated by one occupied even-numbered chair, and such that they are opposite each other. For each way, there are ![]() ways to assign the
ways to assign the ![]() ambassadors to the
ambassadors to the ![]() selected seats.
selected seats.
In the first way, there are ![]() distinct orientations. The
distinct orientations. The ![]() advisors can be placed in any of the
advisors can be placed in any of the ![]() odd-numbered chairs adjacent to the ambassadors, and for each placement, there is exactly one way to assign them to the ambassadors. This means that there are
odd-numbered chairs adjacent to the ambassadors, and for each placement, there is exactly one way to assign them to the ambassadors. This means that there are  total seating arrangements for this way.
total seating arrangements for this way.
In the second way, there are ![]() distinct orientations.
distinct orientations. ![]() advisors can be placed in any of the
advisors can be placed in any of the ![]() chairs adjacent to the "chunk" of
chairs adjacent to the "chunk" of ![]() ambassadors, and
ambassadors, and ![]() advisor can be placed in either of the
advisor can be placed in either of the ![]() chairs adjacent to the "lonely" ambassador. Once again, for each placement, there is exactly one way to assign the advisors to the ambassadors. This means that there are
chairs adjacent to the "lonely" ambassador. Once again, for each placement, there is exactly one way to assign the advisors to the ambassadors. This means that there are  total seating arrangements for this way.
total seating arrangements for this way.
In the third way, there are ![]() distinct orientations. For both "chunks" of
distinct orientations. For both "chunks" of ![]() ambassadors,
ambassadors, ![]() advisors can be placed in any of the
advisors can be placed in any of the ![]() chairs adjacent to them, and once again, there is exactly one way to assign them for each placement. This means that there are
chairs adjacent to them, and once again, there is exactly one way to assign them for each placement. This means that there are  total seating arrangements for this way.
total seating arrangements for this way.
Totalling up the arrangements, there are ![]() total ways to seat the people, and the remainder when
total ways to seat the people, and the remainder when ![]() is divided by
is divided by ![]() is
is ![]() . ~emerald_block
. ~emerald_block
Solution 2
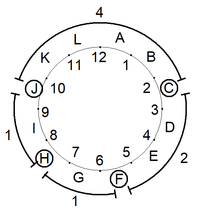
In the diagram, the seats are numbered 1...12. Rather than picking seats for each person, however, each ambassador/assistant team picks a gap between the seats (A...L) and the ambassador sits in the even seat while the assistant sits in the odd seat. For example, if team 1 picks gap C then Ambassador 1 will sit in seat 2 while assistant 1 will sit in seat 3. No two teams can pick adjacent gaps. For example, if team 1 chooses gap C then team 2 cannot pick gaps B or D. In the diagram, the teams have picked gaps C, F, H and J. Note that the gap-gaps - distances between the chosen gaps - (in the diagram, 2, 1, 1, 4) must sum to 8. So, to get the number of seatings, we:
- Choose a gap for team 1 (
 options)
options) - Choose 3 other gaps around the table with positive gap-gaps. Note that because the sum of the distances between the gaps must be equal to
 we create a bijection - to partition the 8 balls into 4 urns, with each urn having a positive number of balls. There is the same as partitioning 4 with 4 non-negative integers, and using stars-and-bars, this is
we create a bijection - to partition the 8 balls into 4 urns, with each urn having a positive number of balls. There is the same as partitioning 4 with 4 non-negative integers, and using stars-and-bars, this is 
- Place the other 3 teams in the chosen gaps (
 permutations)
permutations)
So, the total is ![]() .
.
Therefore, the remainder is ![]() .
.
Solution 3 (PIE)
There are ![]() (placing the ambassadors and then choosing the locations of the advisors) total ways to let everyone sit. However, this may lead to advisors sitting in the same chair, leading to awkward situations. So we find how many ways this happens. There are
(placing the ambassadors and then choosing the locations of the advisors) total ways to let everyone sit. However, this may lead to advisors sitting in the same chair, leading to awkward situations. So we find how many ways this happens. There are  ways to choose which advisors end up sitting together, times
ways to choose which advisors end up sitting together, times ![]() ways to find neighboring even seats (order matters), and for the other two ambassadors, there are
ways to find neighboring even seats (order matters), and for the other two ambassadors, there are  ways to sit and 4 ways for their advisors to sit. This results in
ways to sit and 4 ways for their advisors to sit. This results in ![]() ways for this to happen. However, we overcounted the case when all four of the advisors run out of room to sit, where there are
ways for this to happen. However, we overcounted the case when all four of the advisors run out of room to sit, where there are ![]() to choose the places the ambassadors sit and 4! ways to arrange the ambassadors.
to choose the places the ambassadors sit and 4! ways to arrange the ambassadors. ![]() ways to happen. So the answer is
ways to happen. So the answer is ![]() , which has a remainder of
, which has a remainder of ![]() when divided by 1000.
when divided by 1000.
~minor ![]() fixes by virjoy2001
fixes by virjoy2001
Solution 4
We see that for every 2 adjacent spots on the table, there is exactly one way for an ambassador and his or her partner to sit. There are 2 cases:
- There is an ambassador at the 12th chair and his or her partner at the 1st chair
- There is no pair that has their chairs numbered as 12 and 1
For the first case, there are 3 pairs and 4 empty spaces, which results in ![]() ways to arrange the pairs.
ways to arrange the pairs.
For the second case, there are 4 pairs and 4 empty spaces, which results in ![]() ways to arrange the pairs.
ways to arrange the pairs.
Finally, we have to assign ambassadors and their advisors to the pairs, which has ![]() ways, so
ways, so ![]() , or
, or ![]() ~PenguinMoosey
~PenguinMoosey
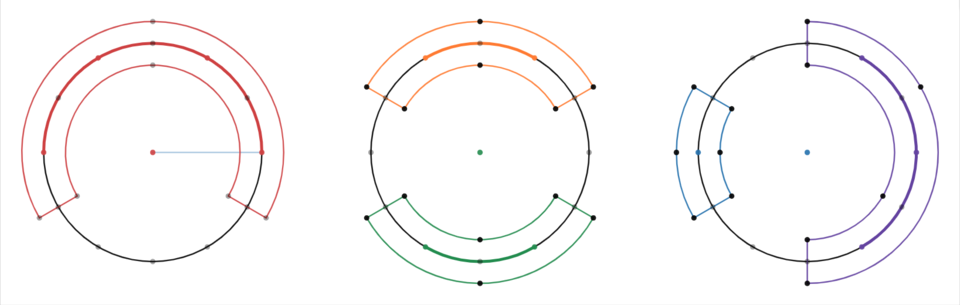
Solution 5 (Lots of diagrams)
Let's begin with a simpler problem. We start with n ambassador chairs in a row and n+1 advisor chairs between them. As before, each advisor has to sit next to his/her ambassador. In the diagram, a black spot represents an ambassador, a blue ring represents an empty advisor seat, and a black dot on top of a blue dot represents an advisor. There are exactly (n+1)! solutions in this case as represented by the diagram. First, let's seat the ambassadors in their positions (n! ways). In the diagram, the first solution is that the advisors all sit an the left of their respective ambassadors. Then, we can slide the rightmost advisor over his/her ambassador to make a new solution. Then, we can do the same with the other advisor next to the empty seat. We can continue this process until all of the advisors sit an the right of their respective ambassadors. In total, there are n!(n+1) = (n+1)! ways.
Now, we are ready to tackle the original problem. If we forget about the numbers and the uniqueness of people, we will have the three configurations shown above. In the first configuration, there is a single red blob of four ambassadors. Let's stretch them out onto a line. Now, it's the same situation as the simpler problem and there are (4+1)! = 5! = 120 ways to seat the people. However, we need to multiply that by 6 because there are 6 orientations. Therefore, we have 720 outcomes for this case. In the second configuration, there is a orange blob and a green blob, each of the case n=2, resulting in (2+1)! * (2+1)! which equals 36. Multiplying the number of orientations, 3, we arrive at 108. Wait! We need to multiply by 6 to account for the many ways that we can choose 2 of the ambassadors to be in the orange blob. Therefore, we have 648 outcomes. Last but not least, we have the final configuration which is a blob of 1 and a blob of 3. Applying the formula results in (1+1)! * (3+1)! which evaluates to 48. Then, we multiply by 4, the number of ways to choose the blobs, and 6, the number of orientations. Our result is 1152. Finally, adding the numbers, we get 2520 and taking mod 1000, we get 520.
See Also
| 2019 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 4 |
Followed by Problem 6 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()