2020 AIME I Problems/Problem 15
Contents
[hide]Problem
Let ![]() be an acute triangle with circumcircle
be an acute triangle with circumcircle ![]() and let
and let ![]() be the intersection of the altitudes of
be the intersection of the altitudes of ![]() Suppose the tangent to the circumcircle of
Suppose the tangent to the circumcircle of ![]() at
at ![]() intersects
intersects ![]() at points
at points ![]() and
and ![]() with
with ![]() and
and ![]() The area of
The area of ![]() can be written in the form
can be written in the form ![]() where
where ![]() and
and ![]() are positive integers, and
are positive integers, and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]()
Solution 1
The following is a power of a point solution to this menace of a problem:
![[asy] defaultpen(fontsize(12)+0.6); size(250); pen p=fontsize(10)+gray+0.4; var phi=75.5, theta=130, r=4.8; pair A=r*dir(270-phi-57), C=r*dir(270+phi-57), B=r*dir(theta-57), H=extension(A,foot(A,B,C),B,foot(B,C,A)); path omega=circumcircle(A,B,C), c=circumcircle(H,B,C); pair O=circumcenter(H,B,C), Op=2*H-O, Z=bisectorpoint(O,Op), X=IP(omega,L(H,Z,0,50)), Y=IP(omega,L(H,Z,50,0)), D=2*H-A, K=extension(B,C,X,Y), E=extension(A,origin,X,Y), L=foot(H,B,C); draw(K--C^^omega^^c^^L(A,D,0,1)); draw(Y--K^^L(A,origin,0,1.5)^^L(X,D,0.7,3.5),fuchsia+0.4); draw(CR(H,length(H-L)),royalblue); draw(C--K,p); dot("$A$",A,dir(120)); dot("$B$",B,down); dot("$C$",C,down); dot("$H$",H,down); dot("$X$",X,up); dot("$Y$",Y,down); dot("$O$",origin,down); dot("$O'$",O,down); dot("$K$",K,up); dot("$L$",L,dir(H-X)); dot("$D$",D,down); dot("$E$",E,down); //draw(O--origin,p); //draw(origin--4*dir(57),fuchsia); //draw(Arc(H,3,160,200),royalblue); //draw(Arc(H,2,30,70),heavygreen); //draw(Arc(H,6,220,240),fuchsia); [/asy]](http://latex.artofproblemsolving.com/2/0/c/20caed74b1a1aac025bf9fc680e1110f795701a8.png) Let points be what they appear as in the diagram below. Note that
Let points be what they appear as in the diagram below. Note that ![]() is not insignificant; from here, we set
is not insignificant; from here, we set ![]() by PoP and trivial construction. Now,
by PoP and trivial construction. Now, ![]() is the reflection of
is the reflection of ![]() over
over ![]() . Note
. Note ![]() , and therefore by Pythagorean theorem we have
, and therefore by Pythagorean theorem we have ![]() . Consider
. Consider ![]() . We have that
. We have that ![]() , and therefore we are ready to PoP with respect to
, and therefore we are ready to PoP with respect to ![]() . Setting
. Setting ![]() , we obtain
, we obtain ![]() by PoP on
by PoP on ![]() , and furthermore, we have
, and furthermore, we have ![]() . Now, we get
. Now, we get ![]() , and from
, and from ![]() we take
we take ![]() However, squaring and manipulating with
However, squaring and manipulating with ![]() yields that
yields that ![]() and from here, since
and from here, since ![]() we get the area to be
we get the area to be ![]() . ~awang11's sol
. ~awang11's sol
Solution 1a
As in the diagram, let ray ![]() extended hits BC at L and the circumcircle at say
extended hits BC at L and the circumcircle at say ![]() . By power of the point at H, we have
. By power of the point at H, we have ![]() . The three values we are given tells us that
. The three values we are given tells us that ![]() . L is the midpoint of
. L is the midpoint of ![]() (see here: https://www.cut-the-knot.org/Curriculum/Geometry/AltitudeAndCircumcircle.shtml ), so
(see here: https://www.cut-the-knot.org/Curriculum/Geometry/AltitudeAndCircumcircle.shtml ), so ![]() .
.
As in the diagram provided, let K be the intersection of ![]() and
and ![]() . By power of a point on the circumcircle of triangle
. By power of a point on the circumcircle of triangle ![]() ,
, ![]() . By power of a point on the circumcircle of triangle
. By power of a point on the circumcircle of triangle ![]() ,
, ![]() , thus
, thus ![]() . Solving gives
. Solving gives ![]() or
or ![]() .
.
By the Pythagorean Theorem on triangle ![]() ,
, ![]() . Now continue with solution 1.
. Now continue with solution 1.
Solution 2
![[asy] size(10cm); pair A, B, C, D, H, K, O, P, L, M, X, Y; A = (-15, 27); B = (-24, 0); C = (24, 0); D = (-8.28, 18.04); O = (0, 7); P = (0, -7); H = (-15, 13); K = (-15, -13); M = (0, 0); L = (-15, 0); X = (-24.9569, 5.53234); Y = (8.39688, 30.5477); draw(circle(O, 25)); draw(circle(P, 25)); draw(A--B--C--cycle); draw(H -- K); draw(A -- O -- P -- H -- cycle); draw(X -- Y); draw(O -- X, dashed); draw(O -- Y, dashed); draw(O -- B, dashed); draw(O -- C, dashed); label("$O$", O, ENE); label("$A$", A, NW); label("$B$", B, W); label("$C$", C, E); label("$H$", H, E); label("$H'$", K, NE); label("$X$", X, W); label("$Y$", Y, NE); label("$O'$", P, E); label("$M$", M, NE); label("$L$", L, NE); label("$D$", D, NNE); label("$2$", X -- H, NW); label("$3$", H -- A, SW); label("$6$", H -- Y, NW); label("$R$", O -- Y, E); dot(O); dot(P); dot(D); dot(H); [/asy]](http://latex.artofproblemsolving.com/9/3/c/93cbdb7042dcdfd8bcc8debd055e6439bd394e78.png) Diagram not to scale.
Diagram not to scale.
We first observe that ![]() , the image of the reflection of
, the image of the reflection of ![]() over line
over line ![]() , lies on circle
, lies on circle ![]() . This is because
. This is because ![]() . This is a well known lemma. The result of this observation is that circle
. This is a well known lemma. The result of this observation is that circle ![]() , the circumcircle of
, the circumcircle of ![]() is the image of circle
is the image of circle ![]() over line
over line ![]() , which in turn implies that
, which in turn implies that ![]() and thus
and thus ![]() is a parallelogram. That
is a parallelogram. That ![]() is a parallelogram implies that
is a parallelogram implies that ![]() is perpendicular to
is perpendicular to ![]() , and thus divides segment
, and thus divides segment ![]() in two equal pieces,
in two equal pieces, ![]() and
and ![]() , of length
, of length ![]() .
.
Using Power of a Point,
![]() This means that
This means that ![]() and
and ![]() , where
, where ![]() is the foot of the altitude from
is the foot of the altitude from ![]() onto
onto ![]() . All that remains to be found is the length of segment
. All that remains to be found is the length of segment ![]() .
.
Looking at right triangle ![]() , we find that
, we find that
![]() Looking at right triangle
Looking at right triangle ![]() , we get the equation
, we get the equation
![]() Plugging in known values, and letting
Plugging in known values, and letting ![]() be the radius of the circle, we find that
be the radius of the circle, we find that
![]()
Recall that ![]() is a parallelogram, so
is a parallelogram, so ![]() . So,
. So, ![]() , where
, where ![]() is the midpoint of
is the midpoint of ![]() . This means that
. This means that
![\[\overline{BC} = 2\overline{BM} = 2\sqrt{R^2 - \left(\frac32\right)^2} = 2\sqrt{\frac{441}{20} - \frac{9}{4}} = \frac{6\sqrt{55}}{5}\]](http://latex.artofproblemsolving.com/5/c/1/5c1a7e3b7fbbbe6efb52c90e25dc8993d9f7ce7c.png)
Thus, the area of triangle ![]() is
is
![]() The answer is
The answer is ![]() .
.
Solution 3 (Official MAA 1)
Extend ![]() to intersect
to intersect ![]() again at
again at ![]() . The Power of a Point Theorem yields
. The Power of a Point Theorem yields ![]() . Because
. Because ![]() , and
, and ![]() and
and ![]() are both complements to
are both complements to ![]() , it follows that
, it follows that ![]() , implying that
, implying that ![]() bisects
bisects ![]() , so the length of the altitude from
, so the length of the altitude from ![]() to
to ![]() is
is ![]() .
.
Let the circumcircle of ![]() be
be ![]() . Because
. Because ![]() , the two triangles must have the same circumradius. Because the circumcircle of
, the two triangles must have the same circumradius. Because the circumcircle of ![]() is
is ![]() , the circles
, the circles ![]() and
and ![]() have the same radius
have the same radius ![]() . Denote the centers of
. Denote the centers of ![]() and
and ![]() by
by ![]() and
and ![]() , respectively, and let
, respectively, and let ![]() be the midpoint of
be the midpoint of ![]() . Note that trapezoid
. Note that trapezoid ![]() has
has ![]() . Also
. Also ![]() and
and ![]() . Because
. Because ![]() is a translation of
is a translation of ![]() in the direction of
in the direction of ![]() , it follows that
, it follows that ![]() . Finally, the Pythagorean Theorem applied to
. Finally, the Pythagorean Theorem applied to ![]() yields
yields ![]() . Let
. Let ![]() be the projection of
be the projection of ![]() onto
onto ![]() . Then
. Then ![]() , so the Pythagorean Theorem applied to
, so the Pythagorean Theorem applied to ![]() yields
yields
![]() Solving for
Solving for ![]() gives
gives ![]() . It follows from properties of the orthocenter
. It follows from properties of the orthocenter ![]() that
that![]() so
so![]() Therefore by the Extended Law of Sines
Therefore by the Extended Law of Sines![]() so
so
![]() The requested sum is
The requested sum is ![]() .
.
![[asy] unitsize(0.6 cm); pair A, B, C, D, H, M, O, Op, P, T, X, Y, Z; real R = 21/(2*sqrt(5)); A = (7/sqrt(5),7/2); O = (0,0); B = intersectionpoint((0,-3/2)--(R,-3/2),Circle(O,R)); C = intersectionpoint((0,-3/2)--(-R,-3/2),Circle(O,R)); H = A + B + C; P = reflect(B,C)*(H); D = (H + P)/2; Op = reflect(B,C)*(O); X = intersectionpoint(H--(H + scale(2)*rotate(90)*(Op - H)), Circle(O,R)); Y = intersectionpoint(H--(H + scale(2)*rotate(90)*(H - Op)), Circle(O,R)); Z = extension(X, Y, B, C); M = (X + Y)/2; T = H + O - M; draw(Circle(O,R)); draw(Circle(Op,R)); draw(A--B--C--cycle); draw(A--P); draw(B--Z--Y); draw(H--Op--O--M); draw(O--T); draw(O--X); dot("$A$", A, NE); dot("$B$", B, SW); dot("$C$", C, W); dot("$D$", D, SW); dot("$H$", H, NE); dot("$M$", M, NE); dot("$O$", O, W); dot("$O'$", Op, W); dot("$P$", P, SE); dot("$T$", T, N); dot("$X$", X, E); dot("$Y$", Y, NW); dot("$Z$", Z, E); label("$\omega$", R*dir(140), dir(140)); label("$\omega'$", Op + R*dir(220), dir(220)); [/asy]](http://latex.artofproblemsolving.com/f/e/8/fe81e76486d086a9421e8b20c94f05408e59f28f.png)
Solution 3a (slightly modified Solution 3)
Note that ![]() bisects
bisects ![]() . Using the same method from Solution 3 we find
. Using the same method from Solution 3 we find ![]() . Let the midpoint of
. Let the midpoint of ![]() be
be ![]() , then by the Pythagorean Theorem we have
, then by the Pythagorean Theorem we have ![]() , so
, so ![]() . Since
. Since ![]() we have that the area of ABC is
we have that the area of ABC is ![]() so the answer is
so the answer is ![]()
~bobjoebilly
Solution 4 (Official MAA 2)
Let ![]() be the intersection point of line
be the intersection point of line ![]() and
and ![]() , noting that
, noting that ![]() . Because the area of
. Because the area of ![]() is
is ![]() , it suffices to compute
, it suffices to compute ![]() and
and ![]() separately. As in the previous solution,
separately. As in the previous solution, ![]() . The value of
. The value of ![]() can be found using the following lemma.
can be found using the following lemma.
Lemma: Triangle ![]() is isosceles with base
is isosceles with base ![]() .
.
Proof: Because the circumcircle of ![]() ,
, ![]() , and
, and ![]() have the same radius, there exists a translation
have the same radius, there exists a translation ![]() sending the former to the latter. Because
sending the former to the latter. Because ![]() is parallel to the line connecting the centers of the two circles,
is parallel to the line connecting the centers of the two circles, ![]() must send
must send ![]() to
to ![]() , meaning
, meaning ![]() also sends
also sends ![]() to the tangent to
to the tangent to ![]() at
at ![]() . But this means that this tangent is parallel to
. But this means that this tangent is parallel to ![]() , which implies the conclusion.
, which implies the conclusion.
Applying Stewart's Theorem to ![]() yields
yields![]() implying
implying ![]()
By the Law of Cosines
![]() so
so![]() Let
Let ![]() be the radius of
be the radius of ![]() . By the Extended Law of Sines
. By the Extended Law of Sines![]() Then the solution proceeds as in Solution 3.
Then the solution proceeds as in Solution 3.
Solution 5 (Official MAA 3)
Define points ![]() and
and ![]() as above, and note that
as above, and note that ![]() and
and ![]() . Let the circumcircle of
. Let the circumcircle of ![]() be
be ![]() .
.
Extend ![]() past
past ![]() until it intersects line
until it intersects line ![]() at point
at point ![]() . Because line
. Because line ![]() is a radical axis of
is a radical axis of ![]() and
and ![]() , it follows from the Power of a Point Theorem that
, it follows from the Power of a Point Theorem that
![]() from which
from which ![]() . By Pythagorean Theorem
. By Pythagorean Theorem ![]() .
.
Let ![]() and
and ![]() . By the Power of a Point Theorem
. By the Power of a Point Theorem
![]() On the other hand,
On the other hand,
![]() from which
from which ![]() . Therefore
. Therefore
![]() Thus
Thus ![]() . Therefore
. Therefore
![]() as above.
as above.
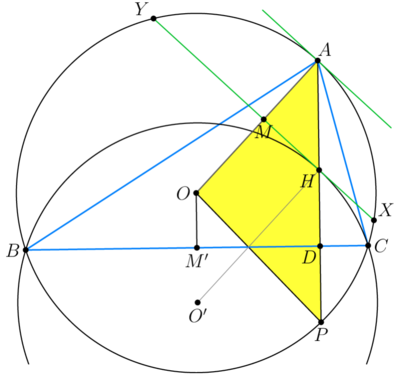
Solution 6
Let ![]() be circumcenter of
be circumcenter of ![]() let
let ![]() be circumradius of
be circumradius of ![]() let
let ![]() be the image of circle
be the image of circle ![]() over line
over line ![]() (the circumcircle of
(the circumcircle of ![]() ).
).
Let ![]() be the image of the reflection of
be the image of the reflection of ![]() over line
over line ![]() lies on circle
lies on circle ![]() Let
Let ![]() be the midpoint of
be the midpoint of ![]() Then
Then ![]() lies on
lies on ![]()
(see here: https://brilliant.org/wiki/triangles-orthocenter/ or https://en.wikipedia.org/wiki/Altitude_(triangle) Russian)
![]() lies on
lies on ![]()
![]() lies on
lies on ![]()
We use properties of crossing chords and get
![]() We use properties of radius perpendicular chord and get
We use properties of radius perpendicular chord and get
![]() We find
We find
![]() We use properties of isosceles
We use properties of isosceles ![]() and find
and find ![]()
We use ![]() and find
and find ![]()
The area of ![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Two Video Solutions by MOP 2024
- https://youtube.com/watch?v=qgM-GbAWXCc (Power of a Point and Symmetry)
- https://youtube.com/watch?v=XOUssYh14aw (Geometric Transformations, Angle Chasing, Trig)
~r00tsOfUnity
Video Solution by On the Spot STEM
https://www.youtube.com/watch?v=L7B20E95s4M
See Also
| 2020 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Problem | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()