2020 AIME I Problems/Problem 6
Contents
[hide]Problem
A flat board has a circular hole with radius ![]() and a circular hole with radius
and a circular hole with radius ![]() such that the distance between the centers of the two holes is
such that the distance between the centers of the two holes is ![]() Two spheres with equal radii sit in the two holes such that the spheres are tangent to each other. The square of the radius of the spheres is
Two spheres with equal radii sit in the two holes such that the spheres are tangent to each other. The square of the radius of the spheres is ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Diagram
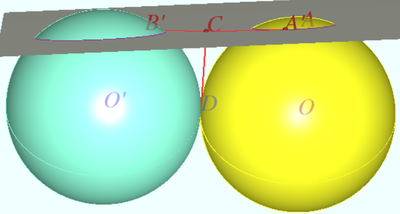
![[asy] /* Made by MRENTHUSIASM */ size(300); import graph3; import solids; currentprojection=orthographic((1,-5,1)); real r = sqrt(160/13); triple C1, C2, B1, B2; C1 = (0,0,sqrt(r^2-1^2)); C2 = (7,0,sqrt(r^2-2^2)); B1 = (0,0,0); B2 = (7,0,0); draw((-5,-10,0)--(-5,10,0)--(12,10,0)--(12,-10,0)--cycle); draw(shift(C1)*scale3(r)*unitsphere,yellow,light=White); draw(shift(C2)*scale3(r)*unitsphere,yellow,light=White); draw(Circle(B1,1,(0,0,1))); draw(Circle(B2,2,(0,0,1))); dot(C1^^C2^^B1^^B2,linewidth(4.5)); [/asy]](http://latex.artofproblemsolving.com/b/b/3/bb3493ac92ddd157a54c88f53fdb25d258a5f123.png) ~MRENTHUSIASM
~MRENTHUSIASM
Solution 1 (Pythagorean Theorem)
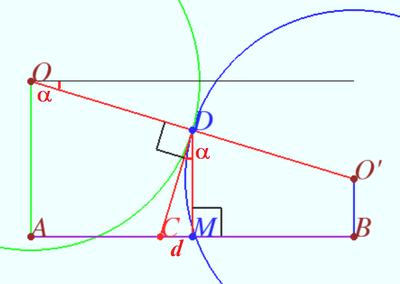
![[asy] size(10cm); pair A, B, C, D, O, P, H, L, X, Y; A = (-1, 0); B = (1, 0); H = (0, 0); C = (5, 0); D = (9, 0); L = (7, 0); O = (0, sqrt(160/13 - 1)); P = (7, sqrt(160/13 - 4)); X = (0, sqrt(160/13 - 4)); Y = (O + P) / 2; draw(A -- O -- B -- cycle); draw(C -- P -- D -- cycle); draw(B -- C); draw(O -- P); draw(P -- X, dashed); draw(O -- H, dashed); draw(P -- L, dashed); draw(circle(O, sqrt(160/13))); draw(circle(P, sqrt(160/13))); path b = brace(L-(0,1), H-(0,1),0.5); draw(b); label("$r$", O -- Y, N); label("$r$", Y -- P, N); label("$r$", O -- A, NW); label("$r$", P -- D, NE); label("$1$", A -- H, N); label("$2$", L -- D, N); label("$7$", b, S); dot(A^^B^^C^^D^^O^^P^^H^^L^^X^^Y,linewidth(4)); [/asy]](http://latex.artofproblemsolving.com/6/3/a/63af3ee78c8a31a2ef396006676d018ab50a0d2f.png) Set the common radius to
Set the common radius to ![]() . First, take the cross section of the sphere sitting in the hole of radius
. First, take the cross section of the sphere sitting in the hole of radius ![]() . If we draw the perpendicular bisector of the chord (the hole) through the circle, this line goes through the center. Connect the center also to where the chord hits the circle, for a right triangle with hypotenuse
. If we draw the perpendicular bisector of the chord (the hole) through the circle, this line goes through the center. Connect the center also to where the chord hits the circle, for a right triangle with hypotenuse ![]() and base
and base ![]() . Therefore, the height of this circle outside of the hole is
. Therefore, the height of this circle outside of the hole is ![]() .
.
The other circle follows similarly for a height (outside the hole) of ![]() . Now, if we take the cross section of the entire board, essentially making it two-dimensional, we can connect the centers of the two spheres, then form another right triangle with base
. Now, if we take the cross section of the entire board, essentially making it two-dimensional, we can connect the centers of the two spheres, then form another right triangle with base ![]() , as given by the problem. The height of this triangle is the difference between the heights of the parts of the two spheres outside the holes, which is
, as given by the problem. The height of this triangle is the difference between the heights of the parts of the two spheres outside the holes, which is ![]() . Now we can set up an equation in terms of
. Now we can set up an equation in terms of ![]() with the Pythagorean theorem:
with the Pythagorean theorem: ![]() Simplifying a few times,
Simplifying a few times,
 Therefore, our answer is
Therefore, our answer is ![]() .
.
~molocyxu
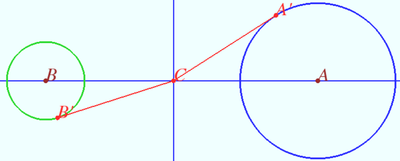
Solution 2 (Tangential Distance)
Let ![]() and
and ![]() be the centers of the holes, let
be the centers of the holes, let ![]() be the point of crossing
be the point of crossing ![]() and radical axes of the circles. So
and radical axes of the circles. So ![]() has equal tangential distance to any point of both spheres. In particular to the circles (https://en.wikipedia.org/wiki/Radical_axis.)
has equal tangential distance to any point of both spheres. In particular to the circles (https://en.wikipedia.org/wiki/Radical_axis.)
![]()
![]()
Let ![]() be the point of tangency of the spheres common radius
be the point of tangency of the spheres common radius ![]() centered at
centered at ![]() and
and ![]() Let
Let ![]() be the angle between
be the angle between ![]() and flat board. In the plane, perpendicular to board
and flat board. In the plane, perpendicular to board ![]()
Distance between ![]() and midpoint
and midpoint ![]() of
of ![]() is
is
![]()
![]()
![\[2R \cos \alpha = AB = 7 \implies R = \frac {\frac{7}{2} } {\frac{7}{2}\sqrt \frac{13}{160}} = \sqrt {\frac{160}{13}}.\]](http://latex.artofproblemsolving.com/f/e/3/fe3b4ac08893261aaa785d9dfa52759e05f997cb.png) Hence the answer is
Hence the answer is ![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Video solution (With Animation)
Video Solution
https://www.youtube.com/watch?v=qCTq8KhZfYQ
See Also
| 2020 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 5 |
Followed by Problem 7 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
These problems are copyrighted © by the Mathematical Association of America, as part of the American Mathematics Competitions. ![]()