2021 Fall AMC 12B Problems/Problem 15
Contents
[hide]Problem
Three identical square sheets of paper each with side length ![]() are stacked on top of each other. The middle sheet is rotated clockwise
are stacked on top of each other. The middle sheet is rotated clockwise ![]() about its center and the top sheet is rotated clockwise
about its center and the top sheet is rotated clockwise ![]() about its center, resulting in the
about its center, resulting in the ![]() -sided polygon shown in the figure below. The area of this polygon can be expressed in the form
-sided polygon shown in the figure below. The area of this polygon can be expressed in the form ![]() , where
, where ![]() ,
, ![]() , and
, and ![]() are positive integers, and
are positive integers, and ![]() is not divisible by the square of any prime. What is
is not divisible by the square of any prime. What is ![]() ?
?
![[asy] defaultpen(fontsize(8)+0.8); size(150); pair O,A1,B1,C1,A2,B2,C2,A3,B3,C3,A4,B4,C4; real x=45, y=90, z=60; O=origin; A1=dir(x); A2=dir(x+y); A3=dir(x+2y); A4=dir(x+3y); B1=dir(x-z); B2=dir(x+y-z); B3=dir(x+2y-z); B4=dir(x+3y-z); C1=dir(x-2z); C2=dir(x+y-2z); C3=dir(x+2y-2z); C4=dir(x+3y-2z); draw(A1--A2--A3--A4--A1, gray+0.25+dashed); filldraw(B1--B2--B3--B4--cycle, white, gray+dashed+linewidth(0.25)); filldraw(C1--C2--C3--C4--cycle, white, gray+dashed+linewidth(0.25)); dot(O); pair P1,P2,P3,P4,Q1,Q2,Q3,Q4,R1,R2,R3,R4; P1=extension(A1,A2,B1,B2); Q1=extension(A1,A2,C3,C4); P2=extension(A2,A3,B2,B3); Q2=extension(A2,A3,C4,C1); P3=extension(A3,A4,B3,B4); Q3=extension(A3,A4,C1,C2); P4=extension(A4,A1,B4,B1); Q4=extension(A4,A1,C2,C3); R1=extension(C2,C3,B2,B3); R2=extension(C3,C4,B3,B4); R3=extension(C4,C1,B4,B1); R4=extension(C1,C2,B1,B2); draw(A1--P1--B2--R1--C3--Q1--A2); draw(A2--P2--B3--R2--C4--Q2--A3); draw(A3--P3--B4--R3--C1--Q3--A4); draw(A4--P4--B1--R4--C2--Q4--A1); [/asy]](http://latex.artofproblemsolving.com/7/e/b/7eb8841b95d6e1c451addf20403c4e540f176116.png)
![]()
Solution 1
![[asy] defaultpen(fontsize(8)+0.8); size(100); pair A=(0,0); pair B=(1.732,3); pair C=(3,3); pair D=(3,1.732); draw(A--(0,3)--C--(3,0)--A, lightgray+dashed); draw(A--B--C--A); draw(A--D--C, gray); label("$A$",A,W); label("$B$",B,N); label("$C$",C,NE); label("$D$",D,E); label("$E$",(0,3),NW); label("$F$",(3,0),E); [/asy]](http://latex.artofproblemsolving.com/6/4/f/64f3c31b5b88bfd1d71ed15cecc5de817a573f8e.png) The
The ![]() -sided polygon is made out of
-sided polygon is made out of ![]() shapes like
shapes like ![]() . Then
. Then ![]() , and
, and ![]() , so
, so ![]() . Then
. Then ![]() ; therefore
; therefore ![]() . Thus
. Thus
![]() and the required area is
and the required area is ![]() . Finally
. Finally ![]() .
~lopkiloinm
.
~lopkiloinm
Note: Drop an altitude from ![]() to
to ![]() to construct point
to construct point ![]() . This creates right triangles. ~erringbubble
. This creates right triangles. ~erringbubble
Solution 2
As shown in Image:2021_AMC_12B_(Nov)_Problem_15,_sol.png, all 12 vertices of three squares form a regular dodecagon (12-gon).
Denote by ![]() the center of this dodecagon.
the center of this dodecagon.
Hence, ![]() .
.
Because the length of a side of a square is 6, ![]() .
.
Hence, ![]() .
.
We notice that ![]() .
Hence,
.
Hence, ![]() .
.
Therefore, the area of the region that three squares cover is

Therefore, the answer is ![]() .
.
~Steven Chen (www.professorchenedu.com)
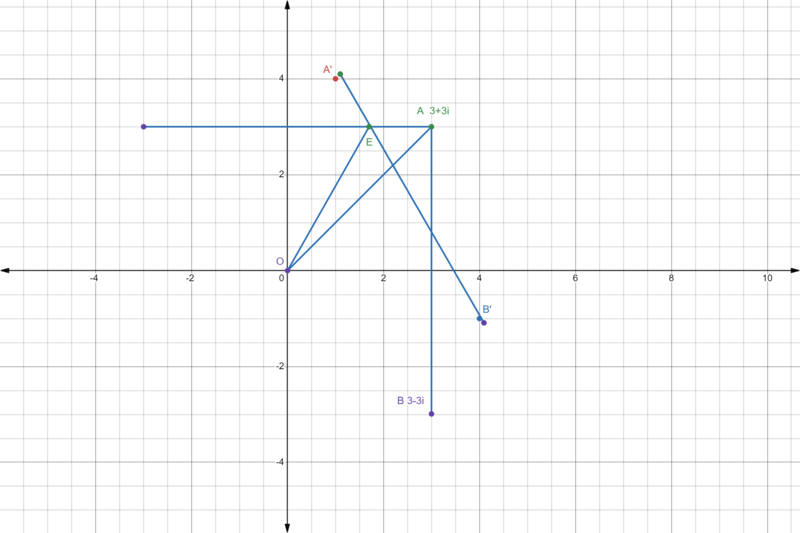
Solution 3 (complex number & coordinate geometry)
set A = 3+3i , A' , B' rotate 30 degree from A, B
A'= A ![]()
line A'B' 
intersect with line y=3 at point ![]() , then length
, then length ![]() ,
,
use shoelace or ![]() = 1/2 * AE * AB/2 = 1/2 *
= 1/2 * AE * AB/2 = 1/2 * ![]() * 3
* 3
total area = 24 * ![]() = = 108 - 36
= = 108 - 36 ![]() the answer is
the answer is ![]() .
.
Video Solution (Just 4 min!)
~Education, the Study of Everything
Video Solution by TheBeautyofMath
~IceMatrix
See Also
| 2021 Fall AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 17 |
Followed by Problem 19 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
| 2021 Fall AMC 12B (Problems • Answer Key • Resources) | |
| Preceded by Problem 14 |
Followed by Problem 16 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()