2022 AIME II Problems/Problem 3
Contents
[hide]Problem
A right square pyramid with volume ![]() has a base with side length
has a base with side length ![]() The five vertices of the pyramid all lie on a sphere with radius
The five vertices of the pyramid all lie on a sphere with radius ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
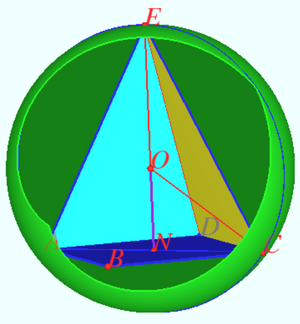
Diagram
![[asy] import three; import settings; leftbutton=new string[] {"rotate","zoom","shift","pan"}; middlebutton=new string[] {""}; rightbutton=new string[] {"zoom","rotateX","rotateY","rotateZ"}; wheelup=new string[] {"zoomin"}; wheeldown=new string[] {"zoomout"}; import three; pen p = rgb("00FF80")+opacity(0.25); pen q = rgb("FF8000")+opacity(0.75); triple A = (-3,-3,0); triple B = (-3,3,0); triple C = (3,3,0); triple D = (3,-3,0); triple F = (0,0,9/2); surface sphere = shift((0,0,1/4))*scale3(17/4)*unitsphere; draw(sphere,p); draw(A--B--C--D--A--F--B--F--C--F--D--F--A,q); dot(A); dot(B); dot(C); dot(D); dot(F); [/asy]](http://latex.artofproblemsolving.com/c/6/4/c64a045f830f45315105799c102d69a5e288a845.png)
Solution 1
Although I can't draw the exact picture of this problem, but it is quite easy to imagine that four vertices of the base of this pyramid is on a circle (Radius ![]() ). Since all five vertices are on the sphere, the distances of the spherical center and the vertices are the same:
). Since all five vertices are on the sphere, the distances of the spherical center and the vertices are the same: ![]() . Because of the symmetrical property of the pyramid,
we can imagine that the line of the apex and the (sphere's) center will intersect the square at the (base's) center.
. Because of the symmetrical property of the pyramid,
we can imagine that the line of the apex and the (sphere's) center will intersect the square at the (base's) center.
Since the volume is ![]() , where
, where ![]() is the height of this pyramid, we have:
is the height of this pyramid, we have: ![]() according to the Pythagorean theorem.
according to the Pythagorean theorem.
Solve this equation will give us ![]() therefore
therefore ![]()
Solution 2
To start, we find the height of the pyramid. By the volume of a pyramid formula, we have ![]() Next, let us find the length of the non-base sides of the pyramid. By the Pythagorean Theorem, noting that the distance from one vertex of the base to the center of the base is
Next, let us find the length of the non-base sides of the pyramid. By the Pythagorean Theorem, noting that the distance from one vertex of the base to the center of the base is ![]() , we have
, we have ![\[x=\sqrt{\left(\frac92\right)^2+(3\sqrt2)^2}=\sqrt{\frac{153}4}=\frac{3\sqrt{17}}2.\]](http://latex.artofproblemsolving.com/7/5/6/7568a8673657eb8699e69661e8c82e765d9b2933.png) Taking the cross section of the pyramid and transforming the problem into
Taking the cross section of the pyramid and transforming the problem into ![]() -d, it suffices to find the radius of the circumcircle of a triangle of side lengths
-d, it suffices to find the radius of the circumcircle of a triangle of side lengths ![]() ,
, ![]() ,
, ![]() . This turns out to be easy by the formula
. This turns out to be easy by the formula ![]() , and through computing this value (the work has been left out) we find that
, and through computing this value (the work has been left out) we find that ![]() , so our answer is
, so our answer is ![]() .
.
~A1001
Solution 3 (Coord bash)
By the volume of a pyramid formula, we have that the height of the pyramid is ![]() . Since the base is a square with side length 6, the simplest way to place it in the coordinate plane is to put the center of the square at the origin and let the base be on the
. Since the base is a square with side length 6, the simplest way to place it in the coordinate plane is to put the center of the square at the origin and let the base be on the ![]() plane. Then, the vertices of the base would be
plane. Then, the vertices of the base would be ![]() in some order. Also, let the vertex be
in some order. Also, let the vertex be ![]() . Recall that the formula for a sphere is
. Recall that the formula for a sphere is ![]() where the center is
where the center is ![]() and the radius is
and the radius is ![]() . Symmetry gives that
. Symmetry gives that ![]() . Plug in
. Plug in ![]() and
and ![]() and you get the system of equation
and you get the system of equation
![]()
![]()
Solving gives ![]() and
and ![]() , so our answer is
, so our answer is ![]() .~Ddk001
.~Ddk001
Solution 4 (Power of a Point)
We know that the volume of a square pyramid is ![]() . The volume of the pyramid is
. The volume of the pyramid is ![]() and the square's side length is
and the square's side length is ![]() . Plugging the information back into the formula, we get
. Plugging the information back into the formula, we get
![]() .
.
By Pythagorean theorem, we can say the diagonal of the square is
![]() .
.
If we draw a line going through the poles of the sphere, we can see that the line perpendicularly bisects the square's diagonal. If we take the cross-section of the sphere making the problem ![]() -d, and call the radius of the sphere
-d, and call the radius of the sphere ![]() , by the power of point, we can say
, by the power of point, we can say
![]()
solving this equation gives you
![]()
so the answer is ![]() . ~Lentarot
. ~Lentarot
Video Solution (Mathematical Dexterity)
https://www.youtube.com/watch?v=UJAYW6YNFVU
Video Solution by Power of Logic
See Also
| 2022 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 2 |
Followed by Problem 4 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()