Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1985 AIME Problems/Problem 4"
 
(14 intermediate revisions by 11 users not shown)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
−
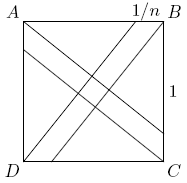
A small [[square (geometry) | square]] is constructed inside a square of [[area]] 1 by dividing each side of the unit square into <math>n</math> equal parts, and then connecting the [[vertex | vertices]] to the division points closest to the opposite vertices. Find the value of <math>n</math> if the the area of the small square is exactly <math>\frac1{1985}</math>.  
+
A small [[square (geometry) | square]] is constructed inside a square of [[area]] 1 by dividing each side of the unit square into <math>n</math> equal parts, and then connecting the [[vertex | vertices]] to the division points closest to the opposite vertices. Find the value of <math>n</math> if the the [[area]] of the small square is exactly <math>\frac1{1985}</math>.  
−
{{image}}
+
 
−
== Solution ==
+
[[Image:AIME_1985_Problem_4.png]]
−
{{solution}}
+
 
 +
== Solution 1==
 +
The lines passing through <math>A</math> and <math>C</math> divide the square into three parts, two [[right triangle]]s and a [[parallelogram]].  Using the smaller side of the parallelogram, <math>1/n</math>, as the base, where the height is 1, we find that the area of the parallelogram is <math>A = \frac{1}{n}</math>.  By the [[Pythagorean Theorem]], the longer base of the parallelogram has [[length]] <math>l = \sqrt{1^2 + \left(\frac{n - 1}{n}\right)^2} = \frac{1}{n}\sqrt{2n^2 - 2n + 1}</math>, so the parallelogram has height <math>h = \frac{A}{l} = \frac{1}{\sqrt{2n^2 - 2n + 1}}</math>.  But the height of the parallelogram is the side of the little square, so <math>2n^2 - 2n + 1 = 1985</math>.  Solving this [[quadratic equation]] gives <math>n = \boxed{32}</math>.
 +
 
 +
==Solution 2==
 +
[[File:Aime.png]]
 +
 
 +
Surrounding the square with area <math>\frac{1}{1985}</math> are <math>4</math> right triangles with hypotenuse <math>1</math> (sides of the large square). Thus, <math>X + \frac{1}{1985} = 1</math>, where <math>X</math> is the area of the of the 4 triangles.
 +
We can thus use proportions to solve this problem.
 +
<cmath>\begin{eqnarray*}
 +
\frac{GF}{BE}=\frac{CG}{CB}\implies
 +
\frac{\frac{1}{\sqrt{1985}}}{BE}=\frac{\frac{1}{n}}{1}\implies
 +
BE=\frac{n\sqrt{1985}}{1985}
 +
\end{eqnarray*}</cmath>
 +
Also,
 +
<cmath>\begin{eqnarray*}
 +
\frac{BE}{1}=\frac{EC}{\frac{n-1}{n}}\implies
 +
EC=\frac{\sqrt{1985}}{1985}(n-1)
 +
\end{eqnarray*}</cmath>
 +
Thus,
 +
<cmath>\begin{eqnarray*}
 +
2(BE)(EC)+\frac{1}{1985}=1\\
 +
2n^{2}-2n+1=1985\\
 +
n(n-1)=992
 +
\end{eqnarray*}</cmath>
 +
Simple factorization and guess and check gives us <math>\boxed{32}</math>.
 +
 
 +
== Solution 3 ==
 +
[[File:AIME_1985_Problem_4_Solution_3_Diagram.png]]
 +
 
 +
Line Segment <math>DE = \frac{1}{n}</math>, so <math>EC = 1 - \frac{1}{n} = \frac{n-1}{n}</math>. Draw line segment <math>HE</math> parallel to the corresponding sides of the small square, <math>HE</math> has length <math>\frac{1}{\sqrt{1985}}</math>, as it is the same length as the sides of the square. Notice that <math>\triangle CEL</math> is similar to <math>\triangle HDE</math> by <math>AA</math> similarity. Thus, <math>\frac{LC}{HE} = \frac{EC}{DE} = n-1</math>, so <math>LC = \frac{n-1}{\sqrt{1985}}</math>. Notice that <math>\triangle CEL</math> is also similar to <math>\triangle CDF</math> by <math>AA</math> similarity. Thus, <math>\frac{FC}{EC} = \frac{DC}{LC}</math>, and the expression simplifies into a quadratic equation <math>n^2 - n - 992 = 0</math>. Solving this quadratic equation yields <math>n =\boxed{32}</math>.
 +
 
 
== See also ==
 
== See also ==
−
* [[1985 AIME Problems/Problem 3 | Previous problem]]
+
{{AIME box|year=1985|num-b=3|num-a=5}}
−
* [[1985 AIME Problems/Problem 5 | Next problem]]
+
* [[AIME Problems and Solutions]]
−
* [[1985 AIME Problems]]
+
* [[American Invitational Mathematics Examination]]
 +
* [[Mathematics competition resources]]
  
 
[[Category: Intermediate Geometry Problems]]
 
[[Category: Intermediate Geometry Problems]]

Latest revision as of 20:40, 2 March 2020

Problem

A small square is constructed inside a square of area 1 by dividing each side of the unit square into $n$ equal parts, and then connecting the vertices to the division points closest to the opposite vertices. Find the value of $n$ if the the area of the small square is exactly $\frac1{1985}$.

AIME 1985 Problem 4.png

Solution 1

The lines passing through $A$ and $C$ divide the square into three parts, two right triangles and a parallelogram. Using the smaller side of the parallelogram, $1/n$, as the base, where the height is 1, we find that the area of the parallelogram is $A = \frac{1}{n}$. By the Pythagorean Theorem, the longer base of the parallelogram has length $l = \sqrt{1^2 + \left(\frac{n - 1}{n}\right)^2} = \frac{1}{n}\sqrt{2n^2 - 2n + 1}$, so the parallelogram has height $h = \frac{A}{l} = \frac{1}{\sqrt{2n^2 - 2n + 1}}$. But the height of the parallelogram is the side of the little square, so $2n^2 - 2n + 1 = 1985$. Solving this quadratic equation gives $n = \boxed{32}$.

Solution 2

Aime.png

Surrounding the square with area $\frac{1}{1985}$ are $4$ right triangles with hypotenuse $1$ (sides of the large square). Thus, $X + \frac{1}{1985} = 1$, where $X$ is the area of the of the 4 triangles. We can thus use proportions to solve this problem. \begin{eqnarray*} \frac{GF}{BE}=\frac{CG}{CB}\implies \frac{\frac{1}{\sqrt{1985}}}{BE}=\frac{\frac{1}{n}}{1}\implies BE=\frac{n\sqrt{1985}}{1985} \end{eqnarray*} Also, \begin{eqnarray*} \frac{BE}{1}=\frac{EC}{\frac{n-1}{n}}\implies EC=\frac{\sqrt{1985}}{1985}(n-1) \end{eqnarray*} Thus, \begin{eqnarray*} 2(BE)(EC)+\frac{1}{1985}=1\\ 2n^{2}-2n+1=1985\\ n(n-1)=992 \end{eqnarray*} Simple factorization and guess and check gives us $\boxed{32}$.

Solution 3

AIME 1985 Problem 4 Solution 3 Diagram.png

Line Segment $DE = \frac{1}{n}$, so $EC = 1 - \frac{1}{n} = \frac{n-1}{n}$. Draw line segment $HE$ parallel to the corresponding sides of the small square, $HE$ has length $\frac{1}{\sqrt{1985}}$, as it is the same length as the sides of the square. Notice that $\triangle CEL$ is similar to $\triangle HDE$ by $AA$ similarity. Thus, $\frac{LC}{HE} = \frac{EC}{DE} = n-1$, so $LC = \frac{n-1}{\sqrt{1985}}$. Notice that $\triangle CEL$ is also similar to $\triangle CDF$ by $AA$ similarity. Thus, $\frac{FC}{EC} = \frac{DC}{LC}$, and the expression simplifies into a quadratic equation $n^2 - n - 992 = 0$. Solving this quadratic equation yields $n =\boxed{32}$.

See also

1985 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 3 		Followed by
Problem 5
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1985_AIME_Problems/Problem_4&oldid=118672"