Difference between revisions of "2006 Cyprus MO/Lyceum/Problems"
(→Problem 11) |
(→Problem 12) |
||
| Line 175: | Line 175: | ||
== Problem 12 == | == Problem 12 == | ||
| + | If <math>f(\alpha,\beta)= | ||
| + | then <math>f(28,17)</math> equals | ||
| + | |||
| + | A. <math>8</math> | ||
| + | |||
| + | B. <math>0</math> | ||
| + | |||
| + | C. <math>11</math> | ||
| + | |||
| + | D. <math>5</math> | ||
| + | |||
| + | E. <math>1</math> | ||
[[2006 Cyprus MO/Lyceum/Problem 12|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 12|Solution]] | ||
Revision as of 10:10, 30 June 2007
Contents
[hide]- 1 Problem 1
- 2 Problem 2
- 3 Problem 3
- 4 Problem 4
- 5 Problem 5
- 6 Problem 6
- 7 Problem 7
- 8 Problem 8
- 9 Problem 9
- 10 Problem 10
- 11 Problem 11
- 12 Problem 12
- 13 Problem 13
- 14 Problem 14
- 15 Problem 15
- 16 Problem 16
- 17 Problem 17
- 18 Problem 18
- 19 Problem 19
- 20 Problem 20
- 21 Problem 21
- 22 Problem 22
- 23 Problem 23
- 24 Problem 24
- 25 Problem 25
- 26 Problem 26
- 27 Problem 27
- 28 Problem 28
- 29 Problem 29
- 30 Problem 30
- 31 See also
Problem 1
A diary industry, in a quantity of milk with $4%$ (Error compiling LaTeX. Unknown error_msg) fat adds a quantity of milk with $1%$ (Error compiling LaTeX. Unknown error_msg) fat and produces ![]() kg of milk with $2%$ (Error compiling LaTeX. Unknown error_msg) fat.
The quantity of milk with $1%$ (Error compiling LaTeX. Unknown error_msg) fat, that was added is (in kg)
kg of milk with $2%$ (Error compiling LaTeX. Unknown error_msg) fat.
The quantity of milk with $1%$ (Error compiling LaTeX. Unknown error_msg) fat, that was added is (in kg)
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 2
The operation ![]() is defined by
is defined by ![]()
![]() .
The value of the expression
.
The value of the expression ![]() is
is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 3
The domain of the function ![]() is
is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 4
Given the function ![]() ,
, ![]() Which of the following is correct, about the graph of
Which of the following is correct, about the graph of ![]() ?
?
A. intersects x-axis
B. touches y-axis
C. touches x-axis
D. has minimum point
E. has maximum point
Problem 5
If both integers ![]() are bigger than 1 and satisfy
are bigger than 1 and satisfy ![]() , then the minimum value of
, then the minimum value of ![]() is
is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 6
The value of the expression ![]() is
is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 7
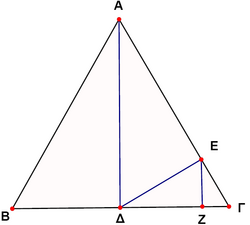
In the figure, ![]() is an equilateral triangle and
is an equilateral triangle and ![]() ,
, ![]() ,
, ![]() . If
. If ![]() , then the length of the side os the triangle ABC is
, then the length of the side os the triangle ABC is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 8
In the figure ![]() is a regular 5-sided polygon and
is a regular 5-sided polygon and ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() are the points of intersections of the extensions of the sides.
If the area of the "star"
are the points of intersections of the extensions of the sides.
If the area of the "star" ![]() is 1, then the area of the shaded quadrilateral
is 1, then the area of the shaded quadrilateral ![]() is
is
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. None of these
Problem 9
If ![]() and
and ![]() , then which of the following is correct
, then which of the following is correct
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. None of these
Problem 10
If ![]() and
and ![]() , then the product
, then the product ![]() equals
equals
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()
Problem 11
Problem 12
If 
then ![]() equals
equals
A. ![]()
B. ![]()
C. ![]()
D. ![]()
E. ![]()