Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2022 AIME II Problems/Problem 2"
Line 2: Line 2:
  
 
Azar, Carl, Jon, and Sergey are the four players left in a singles tennis tournament. They are randomly assigned opponents in the semifinal matches, and the winners of those matches play each other in the final match to determine the winner of the tournament. When Azar plays Carl, Azar will win the match with probability <math>\frac23</math>. When either Azar or Carl plays either Jon or Sergey, Azar or Carl will win the match with probability <math>\frac34</math>. Assume that outcomes of different matches are independent. The probability that Carl will win the tournament is <math>\frac{p}{q}</math>, where <math>p</math> and <math>q</math> are relatively prime positive integers. Find <math>p+q</math>.
 
Azar, Carl, Jon, and Sergey are the four players left in a singles tennis tournament. They are randomly assigned opponents in the semifinal matches, and the winners of those matches play each other in the final match to determine the winner of the tournament. When Azar plays Carl, Azar will win the match with probability <math>\frac23</math>. When either Azar or Carl plays either Jon or Sergey, Azar or Carl will win the match with probability <math>\frac34</math>. Assume that outcomes of different matches are independent. The probability that Carl will win the tournament is <math>\frac{p}{q}</math>, where <math>p</math> and <math>q</math> are relatively prime positive integers. Find <math>p+q</math>.
 +
 +
==Solution 1==
 +
 +
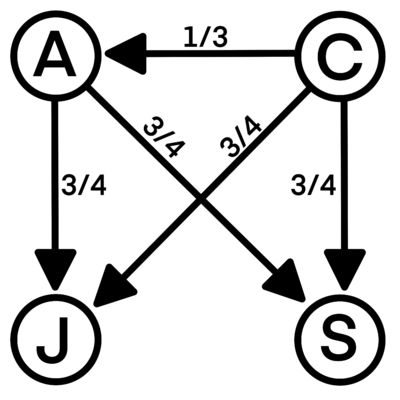
[[File:2022AIMEIIP2.png|400px]]
 +
 +
Let <math>A</math> be Azar, <math>C</math> be Carl, <math>J</math> be Jon, and <math>S</math> be Sergey. This problem can be solved by using <math>2</math> cases.
 +
 +
<math>\textbf{Case 1:}</math> <math>C</math>'s opponent for the semifinals is <math>A</math>
 +
 +
The probability <math>C</math>'s opponent is <math>A</math> is <math>\frac13</math>. Therefore the probability <math>C</math> wins <math>A</math> in the semifinals is <math>\frac13 \cdot \frac13 = \frac19</math>.
 +
The  other semifinal game is played between <math>J</math> and <math>S</math>, it doesn't matter who wins because <math>C</math> has the same probability of winning either one. The probability of <math>C</math> winning in the finals is <math>\frac34</math>, so the probability of <math>C</math> winning the tournament is <math>\frac19 \cdot \frac34 = \frac{1}{12}</math>
 +
 +
 +
<math>\textbf{Case 2:}</math> <math>C</math>'s opponent for the semifinals is <math>J</math> or <math>S</math>
 +
 +
It doesn't matter if <math>C</math>'s opponent is <math>J</math> or <math>S</math> because <math>C</math> has the same probability of winning either one
 +
 +
To be continued......
 +
 +
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
  
 
==Video Solution (Mathematical Dexterity)==
 
==Video Solution (Mathematical Dexterity)==

Revision as of 02:41, 19 February 2022

Problem

Azar, Carl, Jon, and Sergey are the four players left in a singles tennis tournament. They are randomly assigned opponents in the semifinal matches, and the winners of those matches play each other in the final match to determine the winner of the tournament. When Azar plays Carl, Azar will win the match with probability $\frac23$. When either Azar or Carl plays either Jon or Sergey, Azar or Carl will win the match with probability $\frac34$. Assume that outcomes of different matches are independent. The probability that Carl will win the tournament is $\frac{p}{q}$, where $p$ and $q$ are relatively prime positive integers. Find $p+q$.

Solution 1

2022AIMEIIP2.png

Let $A$ be Azar, $C$ be Carl, $J$ be Jon, and $S$ be Sergey. This problem can be solved by using $2$ cases.

$\textbf{Case 1:}$ $C$'s opponent for the semifinals is $A$

The probability $C$'s opponent is $A$ is $\frac13$. Therefore the probability $C$ wins $A$ in the semifinals is $\frac13 \cdot \frac13 = \frac19$. The other semifinal game is played between $J$ and $S$, it doesn't matter who wins because $C$ has the same probability of winning either one. The probability of $C$ winning in the finals is $\frac34$, so the probability of $C$ winning the tournament is $\frac19 \cdot \frac34 = \frac{1}{12}$


$\textbf{Case 2:}$ $C$'s opponent for the semifinals is $J$ or $S$

It doesn't matter if $C$'s opponent is $J$ or $S$ because $C$ has the same probability of winning either one

To be continued......

~isabelchen

Video Solution (Mathematical Dexterity)

https://www.youtube.com/watch?v=C14f91P2pYc

See Also

2022 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 1 		Followed by
Problem 3
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2022_AIME_II_Problems/Problem_2&oldid=171517"