Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2022 AIME II Problems/Problem 11"

(→‎Solution)
Line 2: Line 2:
 
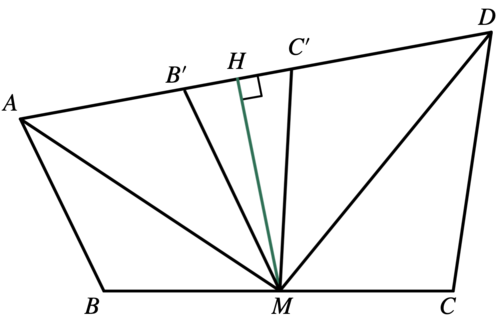
Let <math>ABCD</math> be a convex quadrilateral with <math>AB=2</math>, <math>AD=7</math>, and <math>CD=3</math> such that the bisectors of acute angles <math>\angle{DAB}</math> and <math>\angle{ADC}</math> intersect at the midpoint of <math>\overline{BC}</math>. Find the square of the area of <math>ABCD</math>.
 
Let <math>ABCD</math> be a convex quadrilateral with <math>AB=2</math>, <math>AD=7</math>, and <math>CD=3</math> such that the bisectors of acute angles <math>\angle{DAB}</math> and <math>\angle{ADC}</math> intersect at the midpoint of <math>\overline{BC}</math>. Find the square of the area of <math>ABCD</math>.
  
−
==Solution==
+
==Solution 1==
  
 
[[Image:2022AIME2-Q11.png|thumb|center|500px|2022 AIME II Q11(Hand-draw picture)]]
 
[[Image:2022AIME2-Q11.png|thumb|center|500px|2022 AIME II Q11(Hand-draw picture)]]
Line 29: Line 29:
  
 
~DSAERF-CALMIT (https://binaryphi.site)
 
~DSAERF-CALMIT (https://binaryphi.site)
 +
 +
==Solution 2==
 +
 +
Denote by <math>M</math> the midpoint of segment <math>BC</math>.
 +
Let points <math>P</math> and <math>Q</math> be on segment <math>AD</math>, such that <math>AP = AB</math> and <math>DQ = DC</math>.
 +
 +
Denote <math>\angle DAM = \alpha</math>, <math>\angle BAD = \beta</math>, <math>\angle BMA = \theta</math>, <math>\angle CMD = \phi</math>.
 +
 +
Denote <math>BM = x</math>. Because <math>M</math> is the midpoint of <math>BC</math>, <math>CM = x</math>.
 +
 +
Because <math>AM</math> is the angle bisector of <math>\angle BAD</math> and <math>AB = AP</math>, <math>\triangle BAM \cong \triangle PAM</math>.
 +
Hence, <math>MP = MB</math> and <math>\angle AMP = \theta</math>.
 +
Hence, <math>\angle MPD = \angle MAP + \angle PMA = \alpha + \theta</math>.
 +
 +
Because <math>DM</math> is the angle bisector of <math>\angle CDA</math> and <math>DC = DQ</math>, <math>\triangle CDM \cong \triangle QDM</math>.
 +
Hence, <math>MQ = MC</math> and <math>\angle DMQ = \phi</math>.
 +
Hence, <math>\angle MQA = \angle MDQ + \angle QMD = \beta + \phi</math>.
 +
 +
Because <math>M</math> is the midpoint of segment <math>BC</math>, <math>MB = MC</math>.
 +
Because <math>MP = MB</math> and <math>MQ = MC</math>, <math>MP = MQ</math>.
 +
Thus, <math>\angle MPD = \angle MQA</math>.
 +
Thus,
 +
\[
 +
\alpha + \theta = \beta + \phi . \hspace{1cm} (1)
 +
\]
 +
 +
In <math>\triangle AMD</math>, <math>\angle AMD = 180^\circ - \angle MAD - \angle MDA = 180^\circ - \alpha - \beta</math>.
 +
In addition, <math>\angle AMD = 180^\circ - \angle BMA - \angle CMD = 180^\circ - \theta - \phi</math>.
 +
Thus,
 +
\[
 +
\alpha + \beta = \theta + \phi . \hspace{1cm} (2)
 +
\]
 +
 +
Taking <math>(1) + (2)</math>, we get <math>\alpha = \phi</math>.
 +
Taking <math>(1) - (2)</math>, we get <math>\beta = \theta</math>.
 +
 +
Therefore, <math>\triangle ADM \sim \triangle AMB \sim \triangle MDC</math>.
 +
 +
Hence, <math>\frac{AD}{AM} = \frac{AM}{AB}</math> and <math>\frac{AD}{DM} = \frac{DM}{CD}</math>.
 +
Thus, <math>AM = \sqrt{AD \cdot AD} = \sqrt{14}</math> and <math>DM = \sqrt{AD \cdot CD} = \sqrt{21}</math>.
 +
 +
In <math>\triangle ADM</math>, by applying the law of cosines, <math>\cos \angle AMD  = \frac{AM^2 + DM^2 - AD^2}{2 AM \cdot DM} = - \frac{1}{\sqrt{6}}</math>.
 +
Hence, <math>\sin \angle AMD = \sqrt{1 - \cos^2 \angle AMD} = \frac{\sqrt{5}}{\sqrt{6}}</math>.
 +
Hence, <math>{\rm Area} \ \triangle ADM = \frac{1}{2} AM \cdot DM \dot \sin \angle AMD = \frac{7 \sqrt{5}}{2}</math>.
 +
 +
Therefore,
 +
\begin{align*}
 +
{\rm Area} \ ABCD & = {\rm Area} \ \triangle AMD + {\rm Area} \ \triangle ABM + {\rm Area} \ \triangle MCD \\
 +
& = {\rm Area} \ \triangle AMD \left( 1 + \left( \frac{AM}{AD} \right)^2 + \left( \frac{MD}{AD} \right)^2 \right) \\
 +
& = 6 \sqrt{5} .
 +
\end{align*}
 +
 +
Therefore, the square of <math>{\rm Area} \ ABCD</math> is <math>\left( 6 \sqrt{5} \right)^2 = \boxed{\textbf{(180) }}</math>.
 +
 +
~Steven Chen (www.professorchenedu.com)
  
 
==See Also==
 
==See Also==
 
{{AIME box|year=2022|n=II|num-b=10|num-a=12}}
 
{{AIME box|year=2022|n=II|num-b=10|num-a=12}}
 
{{MAA Notice}}
 
{{MAA Notice}}

Revision as of 13:48, 19 February 2022

Problem

Let $ABCD$ be a convex quadrilateral with $AB=2$, $AD=7$, and $CD=3$ such that the bisectors of acute angles $\angle{DAB}$ and $\angle{ADC}$ intersect at the midpoint of $\overline{BC}$. Find the square of the area of $ABCD$.

Solution 1

2022 AIME II Q11(Hand-draw picture)


According to the problem, we have $AB=AB'=2$, $DC=DC'=3$, $MB=MB'$, $MC=MC'$, and $B'C'=7-2-3=2$

Because $M$ is the midpoint of $BC$, we have $BM=MC$, so: \[MB=MB'=MC'=MC.\]

Then, we can see that $\bigtriangleup{MB'C'}$ is an isosceles triangle with $MB'=MC'$

Therefore, we could start our angle chasing: $\angle{MB'C'}=\angle{MC'B'}=180^\circ-\angle{MC'D}=180^\circ-\angle{MCD}$.

This is when we found that points $M$, $C$, $D$, and $B'$ are on a circle. Thus, $\angle{BMB'}=\angle{CDC'} \Rightarrow \angle{B'MA}=\angle{C'DM}$. This is the time we found that $\bigtriangleup{AB'M} \sim \bigtriangleup{MC'D}$.

Thus, $\frac{AB'}{B'M}=\frac{MC'}{C'D} \Longrightarrow (BM')^2=AB' \cdot C'D = 6$

Point $H$ is the midpoint of $B'C'$, and $MH \perp AD$. $B'H=HC'=1 \Longrightarrow MH=\sqrt{B'M^2-B'H^2}=\sqrt{6-1}=\sqrt{5}$.

The area of this quadrilateral is the sum of areas of triangles: \[S_{\bigtriangleup{ABM}}+S_{\bigtriangleup{AB'M}}+S_{\bigtriangleup{CDM}}+S_{\bigtriangleup{CD'M}}+S_{\bigtriangleup{B'C'M}}\] \[=S_{\bigtriangleup{AB'M}}\cdot 2 + S_{\bigtriangleup{B'C'M}} + S_{\bigtriangleup{C'DM}}\cdot 2\] \[=2 \cdot \frac{1}{2} \cdot AB' \cdot MH + \frac{1}{2} \cdot B'C' \cdot MH + 2 \cdot \frac{1}{2} \cdot C'D \cdot MH\] \[=2\sqrt{5}+\sqrt{5}+3\sqrt{5}=6\sqrt{5}\]

Finally, the square of the area is $(6\sqrt{5})^2=\boxed{180}$

~DSAERF-CALMIT (https://binaryphi.site)

Solution 2

Denote by $M$ the midpoint of segment $BC$. Let points $P$ and $Q$ be on segment $AD$, such that $AP = AB$ and $DQ = DC$.

Denote $\angle DAM = \alpha$, $\angle BAD = \beta$, $\angle BMA = \theta$, $\angle CMD = \phi$.

Denote $BM = x$. Because $M$ is the midpoint of $BC$, $CM = x$.

Because $AM$ is the angle bisector of $\angle BAD$ and $AB = AP$, $\triangle BAM \cong \triangle PAM$. Hence, $MP = MB$ and $\angle AMP = \theta$. Hence, $\angle MPD = \angle MAP + \angle PMA = \alpha + \theta$.

Because $DM$ is the angle bisector of $\angle CDA$ and $DC = DQ$, $\triangle CDM \cong \triangle QDM$. Hence, $MQ = MC$ and $\angle DMQ = \phi$. Hence, $\angle MQA = \angle MDQ + \angle QMD = \beta + \phi$.

Because $M$ is the midpoint of segment $BC$, $MB = MC$. Because $MP = MB$ and $MQ = MC$, $MP = MQ$. Thus, $\angle MPD = \angle MQA$. Thus, \[ \alpha + \theta = \beta + \phi . \hspace{1cm} (1) \]

In $\triangle AMD$, $\angle AMD = 180^\circ - \angle MAD - \angle MDA = 180^\circ - \alpha - \beta$. In addition, $\angle AMD = 180^\circ - \angle BMA - \angle CMD = 180^\circ - \theta - \phi$. Thus, \[ \alpha + \beta = \theta + \phi . \hspace{1cm} (2) \]

Taking $(1) + (2)$, we get $\alpha = \phi$. Taking $(1) - (2)$, we get $\beta = \theta$.

Therefore, $\triangle ADM \sim \triangle AMB \sim \triangle MDC$.

Hence, $\frac{AD}{AM} = \frac{AM}{AB}$ and $\frac{AD}{DM} = \frac{DM}{CD}$. Thus, $AM = \sqrt{AD \cdot AD} = \sqrt{14}$ and $DM = \sqrt{AD \cdot CD} = \sqrt{21}$.

In $\triangle ADM$, by applying the law of cosines, $\cos \angle AMD = \frac{AM^2 + DM^2 - AD^2}{2 AM \cdot DM} = - \frac{1}{\sqrt{6}}$. Hence, $\sin \angle AMD = \sqrt{1 - \cos^2 \angle AMD} = \frac{\sqrt{5}}{\sqrt{6}}$. Hence, ${\rm Area} \ \triangle ADM = \frac{1}{2} AM \cdot DM \dot \sin \angle AMD = \frac{7 \sqrt{5}}{2}$.

Therefore, \begin{align*} {\rm Area} \ ABCD & = {\rm Area} \ \triangle AMD + {\rm Area} \ \triangle ABM + {\rm Area} \ \triangle MCD \\ & = {\rm Area} \ \triangle AMD \left( 1 + \left( \frac{AM}{AD} \right)^2 + \left( \frac{MD}{AD} \right)^2 \right) \\ & = 6 \sqrt{5} . \end{align*}

Therefore, the square of ${\rm Area} \ ABCD$ is $\left( 6 \sqrt{5} \right)^2 = \boxed{\textbf{(180) }}$.

~Steven Chen (www.professorchenedu.com)

See Also

2022 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 10 		Followed by
Problem 12
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2022_AIME_II_Problems/Problem_11&oldid=171581"