Difference between revisions of "2022 AIME II Problems/Problem 15"
(→Solution 3) |
(→Solution 3) |
||
| Line 273: | Line 273: | ||
<cmath>\tan \alpha =\frac { \sin 2 \alpha}{1+\cos 2 \alpha} = \frac {4/5}{1 - 3/5}=2.</cmath> | <cmath>\tan \alpha =\frac { \sin 2 \alpha}{1+\cos 2 \alpha} = \frac {4/5}{1 - 3/5}=2.</cmath> | ||
| − | Semiperimeter of <math>\triangle B'O_2 D </math> is <math> | + | Semiperimeter of <math>\triangle B'O_2 D </math> is <math>s = \frac {15 + \sqrt{193}}{2}.</math> |
| − | The distance from the vertex <math>O_2</math> to the tangent points of the inscribed circle of the triangle <math>B'O_2 D</math> is equal <math> | + | The distance from the vertex <math>O_2</math> to the tangent points of the inscribed circle of the triangle <math>B'O_2 D</math> is equal <math>s – B'D = \frac{15 – \sqrt{193}}{2}.</math> |
| − | The radius of the inscribed circle is <math>r = ( | + | The radius of the inscribed circle is <math>r = (s – B'D) \tan \alpha.</math> |
| − | The area of triangle <math>B'O_2 D</math> is <math> | + | The area of triangle <math>B'O_2 D</math> is <math>[B'O_2 D] = sr = s (s – B'D) \tan \alpha = \frac {15^2 – 193}{2} = 16.</math> |
The hexagon <math>ABO_1 CDO_2</math> has the same area as hexagon <math>B'A'O_1 CDO_2.</math> | The hexagon <math>ABO_1 CDO_2</math> has the same area as hexagon <math>B'A'O_1 CDO_2.</math> | ||
Revision as of 12:42, 18 June 2022
Contents
[hide]Problem
Two externally tangent circles ![]() and
and ![]() have centers
have centers ![]() and
and ![]() , respectively. A third circle
, respectively. A third circle ![]() passing through
passing through ![]() and
and ![]() intersects
intersects ![]() at
at ![]() and
and ![]() and
and ![]() at
at ![]() and
and ![]() , as shown. Suppose that
, as shown. Suppose that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() is a convex hexagon. Find the area of this hexagon.
is a convex hexagon. Find the area of this hexagon.
![[asy] import geometry; size(10cm); point O1=(0,0),O2=(15,0),B=9*dir(30); circle w1=circle(O1,9),w2=circle(O2,6),o=circle(O1,O2,B); point A=intersectionpoints(o,w2)[1],D=intersectionpoints(o,w2)[0],C=intersectionpoints(o,w1)[0]; filldraw(A--B--O1--C--D--O2--cycle,0.2*red+white,black); draw(w1); draw(w2); draw(O1--O2,dashed); draw(o); dot(O1); dot(O2); dot(A); dot(D); dot(C); dot(B); label("$\omega_1$",8*dir(110),SW); label("$\omega_2$",5*dir(70)+(15,0),SE); label("$O_1$",O1,W); label("$O_2$",O2,E); label("$B$",B,N+1/2*E); label("$A$",A,N+1/2*W); label("$C$",C,S+1/4*W); label("$D$",D,S+1/4*E); label("$15$",midpoint(O1--O2),N); label("$16$",midpoint(C--D),N); label("$2$",midpoint(A--B),S); label("$\Omega$",o.C+(o.r-1)*dir(270)); [/asy]](http://latex.artofproblemsolving.com/7/4/a/74a9883958ea503b78cb2c07bc71aefe4d830ce9.png)
Solution 1
First observe that ![]() and
and ![]() . Let points
. Let points ![]() and
and ![]() be the reflections of
be the reflections of ![]() and
and ![]() , respectively, about the perpendicular bisector of
, respectively, about the perpendicular bisector of ![]() . Then quadrilaterals
. Then quadrilaterals ![]() and
and ![]() are congruent, so hexagons
are congruent, so hexagons ![]() and
and ![]() have the same area. Furthermore, triangles
have the same area. Furthermore, triangles ![]() and
and ![]() are congruent, so
are congruent, so ![]() and quadrilateral
and quadrilateral ![]() is an isosceles trapezoid.
is an isosceles trapezoid.
![[asy] import olympiad; size(180); defaultpen(linewidth(0.7)); pair Bp = dir(105), Ap = dir(75), O1 = dir(25), C = dir(320), D = dir(220), O2 = dir(175); draw(unitcircle^^Bp--Ap--O1--C--D--O2--cycle); label("$B'$",Bp,dir(origin--Bp)); label("$A'$",Ap,dir(origin--Ap)); label("$O_1$",O1,dir(origin--O1)); label("$C$",C,dir(origin--C)); label("$D$",D,dir(origin--D)); label("$O_2$",O2,dir(origin--O2)); draw(O2--O1,linetype("4 4")); draw(Bp--D^^Ap--C,linetype("2 2")); [/asy]](http://latex.artofproblemsolving.com/8/d/7/8d777e11cf1e82712d37d5839537f1b3d5e93c03.png) Next, remark that
Next, remark that ![]() , so quadrilateral
, so quadrilateral ![]() is also an isosceles trapezoid; in turn,
is also an isosceles trapezoid; in turn, ![]() , and similarly
, and similarly ![]() . Thus, Ptolmey's theorem on
. Thus, Ptolmey's theorem on ![]() yields
yields ![]() , whence
, whence ![]() . Let
. Let ![]() . The Law of Cosines on triangle
. The Law of Cosines on triangle ![]() yields
yields
![]() and hence
and hence ![]() . Thus the distance between bases
. Thus the distance between bases ![]() and
and ![]() is
is ![]() (in fact,
(in fact, ![]() is a
is a ![]() triangle with a
triangle with a ![]() triangle removed), which implies the area of
triangle removed), which implies the area of ![]() is
is ![]() .
.
Now let ![]() and
and ![]() ; the tangency of circles
; the tangency of circles ![]() and
and ![]() implies
implies ![]() . Furthermore, angles
. Furthermore, angles ![]() and
and ![]() are opposite angles in cyclic quadrilateral
are opposite angles in cyclic quadrilateral ![]() , which implies the measure of angle
, which implies the measure of angle ![]() is
is ![]() . Therefore, the Law of Cosines applied to triangle
. Therefore, the Law of Cosines applied to triangle ![]() yields
yields

Thus ![]() , and so the area of triangle
, and so the area of triangle ![]() is
is ![]() .
.
Thus, the area of hexagon ![]() is
is ![]() .
.
~djmathman
Solution 2
Denote by ![]() the center of
the center of ![]() .
Denote by
.
Denote by ![]() the radius of
the radius of ![]() .
.
We have ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() are all on circle
are all on circle ![]() .
.
Denote ![]() .
Denote
.
Denote ![]() .
Denote
.
Denote ![]() .
.
Because ![]() and
and ![]() are on circles
are on circles ![]() and
and ![]() ,
, ![]() is a perpendicular bisector of
is a perpendicular bisector of ![]() . Hence,
. Hence, ![]() .
.
Because ![]() and
and ![]() are on circles
are on circles ![]() and
and ![]() ,
, ![]() is a perpendicular bisector of
is a perpendicular bisector of ![]() . Hence,
. Hence, ![]() .
.
In ![]() ,
,
![]()
Hence,
![]()
In ![]() ,
,

Hence,
![]()
In ![]() ,
,

Hence,
![]()
Taking ![]() , we get
, we get ![]() .
Thus,
.
Thus, ![]() .
.
Taking these into (1), we get ![]() .
Hence,
.
Hence,

Hence, ![]() .
.
In ![]() ,
,
![]()
In ![]() , by applying the law of sines, we get
, by applying the law of sines, we get
![]()
Because circles ![]() and
and ![]() are externally tangent,
are externally tangent, ![]() is on circle
is on circle ![]() ,
, ![]() is on circle
is on circle ![]() ,
,

Thus, ![]() .
.
Now, we compute ![]() and
and ![]() .
.
Recall ![]() and
and ![]() .
Thus,
.
Thus, ![]() .
.
We also have

Thus,

Therefore,

~Steven Chen (www.professorchenedu.com)
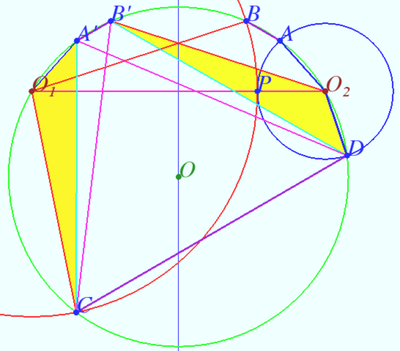
Solution 3
Let points ![]() and
and ![]() be the reflections of
be the reflections of ![]() and
and ![]() respectively, about the perpendicular bisector of
respectively, about the perpendicular bisector of ![]()
![]()
![]() We establish the equality of the arcs and conclude that the corresponding chords are equal
We establish the equality of the arcs and conclude that the corresponding chords are equal
![]()
![]() Similarly
Similarly ![]()
Ptolmey's theorem on ![]() yields
yields ![]()
![]() The area of the trapezoid
The area of the trapezoid ![]() is equal to the area of an isosceles triangle with sides
is equal to the area of an isosceles triangle with sides
![]() and
and ![]()
The height of this triangle is ![]() The area of
The area of ![]() is
is ![]()
![]()
![]()
Denote ![]()
![]() hence
hence ![]()
![]()
Semiperimeter of ![]() is
is ![]()
The distance from the vertex ![]() to the tangent points of the inscribed circle of the triangle
to the tangent points of the inscribed circle of the triangle ![]() is equal
is equal ![]()
The radius of the inscribed circle is ![]()
The area of triangle ![]() is
is ![]()
The hexagon ![]() has the same area as hexagon
has the same area as hexagon ![]()
The area of hexagon ![]() is equal to the sum of the area of the trapezoid
is equal to the sum of the area of the trapezoid ![]() and the areas of two equal triangles
and the areas of two equal triangles ![]() and
and ![]() so the area of the hexagon
so the area of the hexagon ![]() is
is ![]()
Shelomovskii, vvsss, www.deoma-cmd.ru
See Also
| 2022 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Problem | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.