Difference between revisions of "2019 AIME II Problems/Problem 15"
(→Solution 4 (Clean)) |
m (→Solution 4 (Clean)) |
||
| Line 81: | Line 81: | ||
==Solution 4 (Clean)== | ==Solution 4 (Clean)== | ||
| − | [[File: | + | [[File:AIME-II-2019-15.png|400px|right]] |
This solution is directly based of @CantonMathGuy's solution. | This solution is directly based of @CantonMathGuy's solution. | ||
We start off with a key claim. | We start off with a key claim. | ||
Revision as of 11:17, 26 December 2022
Contents
[hide]Problem
In acute triangle ![]() points
points ![]() and
and ![]() are the feet of the perpendiculars from
are the feet of the perpendiculars from ![]() to
to ![]() and from
and from ![]() to
to ![]() , respectively. Line
, respectively. Line ![]() intersects the circumcircle of
intersects the circumcircle of ![]() in two distinct points,
in two distinct points, ![]() and
and ![]() . Suppose
. Suppose ![]() ,
, ![]() , and
, and ![]() . The value of
. The value of ![]() can be written in the form
can be written in the form ![]() where
where ![]() and
and ![]() are positive integers, and
are positive integers, and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]() .
.
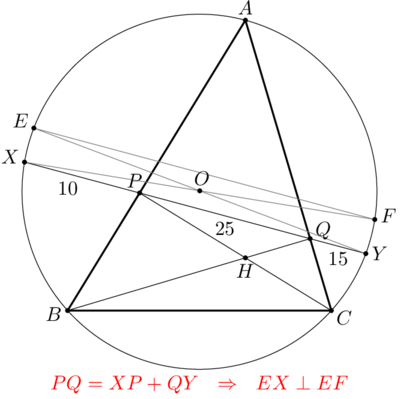
Diagram
![[asy] size(200); defaultpen(linewidth(0.4)+fontsize(10)); pen s = linewidth(0.8)+fontsize(8); pair A,B,C,P,Q,X,Y,O; O = origin; real theta = 32; A = dir(180+theta); B = dir(-theta); C = dir(75); Q = foot(B,A,C); P = foot(C,A,B); path c = circumcircle(A,B,C); X = IP(c, Q--(2*P-Q)); Y = IP(c, P--(2*Q-P)); draw(A--B--C--A, black+0.8); draw(c^^X--Y^^B--Q^^C--P); dot("$A$", A, SW); dot("$B$", B, SE); dot("$C$", C, N); dot("$P$", P, SW); dot("$Q$", Q, W); dot("$X$", X, SE); dot("$Y$", Y, NW); label("$25$", P--Q, SW); label("$15$", Q--Y, SW); label("$10$", X--P, SW); [/asy]](http://latex.artofproblemsolving.com/0/b/9/0b96efb71a1d1aef4a0c2f0c402c8d9d0e29cee0.png)
Solution 1
First we have ![]() , and
, and ![]() by PoP. Similarly,
by PoP. Similarly, ![]() and dividing these each by
and dividing these each by ![]() gives
gives
![]() .
.
It is known that the sides of the orthic triangle are ![]() , and its angles are
, and its angles are ![]() ,
,![]() , and
, and ![]() . We thus have the three sides of the orthic triangle now.
Letting
. We thus have the three sides of the orthic triangle now.
Letting ![]() be the foot of the altitude from
be the foot of the altitude from ![]() , we have, in
, we have, in ![]() ,
,
![]()
![]() similarly, we get
similarly, we get
![]() To finish,
To finish, ![]() The requested sum is
The requested sum is ![]() .
.
༺\ crazyeyemoody9❂7 //༻
Solution 2
Let ![]() ,
, ![]() , and
, and ![]() . Let
. Let ![]() . Then
. Then ![]() and
and ![]() .
.
By Power of a Point theorem,
![]() Thus
Thus ![]() . Then
. Then ![]() ,
, ![]() , and
, and
![]() Use the Law of Cosines in
Use the Law of Cosines in ![]() to get
to get ![]() , which rearranges to
, which rearranges to ![]() Upon simplification, this reduces to a linear equation in
Upon simplification, this reduces to a linear equation in ![]() , with solution
, with solution ![]() . Then
. Then ![]() So the final answer is
So the final answer is ![]()
By SpecialBeing2017
Solution 3
Let ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . By Power of a Point,
. By Power of a Point,
![]() Points
Points ![]() and
and ![]() lie on the circle,
lie on the circle, ![]() , with diameter
, with diameter ![]() , and pow
, and pow![]() , so
, so ![]() Use Law of Cosines in
Use Law of Cosines in ![]() to get
to get ![]() ; since
; since ![]() , this simplifies as
, this simplifies as
![]() We get
We get ![]() and thus
and thus
![]() Therefore
Therefore ![]() . So the answer is
. So the answer is ![]()
By asr41
Solution 4 (Clean)
This solution is directly based of @CantonMathGuy's solution. We start off with a key claim.
Claim. ![]() and
and ![]() .
.
Proof.
Let ![]() and
and ![]() denote the reflections of the orthocenter over points
denote the reflections of the orthocenter over points ![]() and
and ![]() , respectively. Since
, respectively. Since
![]() and
and ![]() ,
,
we have that ![]() is a rectangle.
is a rectangle.
Then, since ![]() we obtain
we obtain ![]() (which directly follows from
(which directly follows from ![]() being cyclic);
being cyclic);
hence ![]() , or
, or ![]() .
.
Similarly, we can obtain ![]() .
.
A direct result of this claim is that ![]() .
.
Thus, we can set ![]() and
and ![]() , then applying Power of a Point on
, then applying Power of a Point on ![]() we get
we get ![]() . Also, we can set
. Also, we can set ![]() and
and ![]() and once again applying Power of a Point (but this time to
and once again applying Power of a Point (but this time to ![]() ) we get
) we get ![]() . Hence,
. Hence, ![]() and the answer is
and the answer is ![]() . ~rocketsri
. ~rocketsri
See Also
| 2019 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()