Difference between revisions of "2019 AIME II Problems/Problem 15"
m (→Solution 4 (Clean)) |
m (→Solution 4 (Clean)) |
||
| Line 81: | Line 81: | ||
==Solution 4 (Clean)== | ==Solution 4 (Clean)== | ||
| − | |||
This solution is directly based of @CantonMathGuy's solution. | This solution is directly based of @CantonMathGuy's solution. | ||
We start off with a key claim. | We start off with a key claim. | ||
| − | |||
<i> Claim. </i> <math>XB \parallel AC</math> and <math>YC \parallel AB</math>. | <i> Claim. </i> <math>XB \parallel AC</math> and <math>YC \parallel AB</math>. | ||
<i> Proof. </i> | <i> Proof. </i> | ||
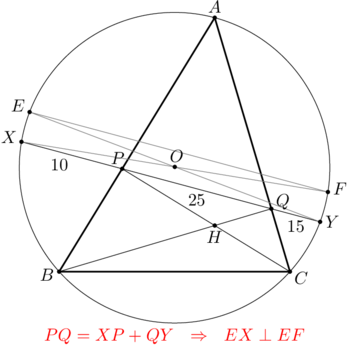
| + | [[File:AIME-II-2019-15.png|350px|right]] | ||
Let <math>E</math> and <math>F</math> denote the reflections of the orthocenter over points <math>P</math> and <math>Q</math>, respectively. Since <math>EF \parallel XY</math> and <cmath>EF = 2 PQ = XP + PQ + QY = XY,</cmath> we have that <math>E X Y F</math> is a rectangle. Then, since <math>\angle XYF = 90^\circ</math> we obtain <math>\angle XBF = 90^\circ</math> (which directly follows from <math>XBYF</math> being cyclic); hence <math>\angle XBQ = \angle AQB</math>, or <math>XB \parallel AQ \Rightarrow XB \parallel AC</math>. | Let <math>E</math> and <math>F</math> denote the reflections of the orthocenter over points <math>P</math> and <math>Q</math>, respectively. Since <math>EF \parallel XY</math> and <cmath>EF = 2 PQ = XP + PQ + QY = XY,</cmath> we have that <math>E X Y F</math> is a rectangle. Then, since <math>\angle XYF = 90^\circ</math> we obtain <math>\angle XBF = 90^\circ</math> (which directly follows from <math>XBYF</math> being cyclic); hence <math>\angle XBQ = \angle AQB</math>, or <math>XB \parallel AQ \Rightarrow XB \parallel AC</math>. | ||
| Line 96: | Line 95: | ||
A direct result of this claim is that <math>\triangle BPX \sim \triangle APQ \sim \triangle CYQ</math>. | A direct result of this claim is that <math>\triangle BPX \sim \triangle APQ \sim \triangle CYQ</math>. | ||
| − | Thus, we can set <math>AP = 5k</math> and <math>BP = 2k</math>, then applying Power of a Point on <math>P</math> we get <math>10 \cdot 40 = 10k^2 \implies k = 2\sqrt{10} \implies AB = 14 \sqrt{10}</math>. Also, we can set <math>AQ = 5l</math> and <math>CQ = 3l</math> and once again applying Power of a Point (but this time to <math>Q</math>) we get <math>15 \cdot 35 = 15l^2 \implies l = \sqrt{35} \implies AC = 8 \sqrt{35}</math>. Hence, | + | Thus, we can set <math>AP = 5k</math> and <math>BP = 2k</math>, then applying Power of a Point on <math>P</math> we get <math>10 \cdot 40 = 10k^2 \implies k = 2\sqrt{10} \implies AB = 14 \sqrt{10}</math>. Also, we can set <math>AQ = 5l</math> and <math>CQ = 3l</math> and once again applying Power of a Point (but this time to <math>Q</math>) we get |
| + | |||
| + | <math>\phantom{...................}15 \cdot 35 = 15l^2 \implies l = \sqrt{35} \implies AC = 8 \sqrt{35}</math>. | ||
| + | |||
| + | Hence, | ||
<math>\phantom{...................}AB \cdot AC = 112 \sqrt{350} = 112 \cdot 5 \sqrt{14} = 560 \sqrt{14}</math> | <math>\phantom{...................}AB \cdot AC = 112 \sqrt{350} = 112 \cdot 5 \sqrt{14} = 560 \sqrt{14}</math> | ||
Revision as of 11:25, 26 December 2022
Contents
[hide]Problem
In acute triangle ![]() points
points ![]() and
and ![]() are the feet of the perpendiculars from
are the feet of the perpendiculars from ![]() to
to ![]() and from
and from ![]() to
to ![]() , respectively. Line
, respectively. Line ![]() intersects the circumcircle of
intersects the circumcircle of ![]() in two distinct points,
in two distinct points, ![]() and
and ![]() . Suppose
. Suppose ![]() ,
, ![]() , and
, and ![]() . The value of
. The value of ![]() can be written in the form
can be written in the form ![]() where
where ![]() and
and ![]() are positive integers, and
are positive integers, and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]() .
.
Diagram
![[asy] size(200); defaultpen(linewidth(0.4)+fontsize(10)); pen s = linewidth(0.8)+fontsize(8); pair A,B,C,P,Q,X,Y,O; O = origin; real theta = 32; A = dir(180+theta); B = dir(-theta); C = dir(75); Q = foot(B,A,C); P = foot(C,A,B); path c = circumcircle(A,B,C); X = IP(c, Q--(2*P-Q)); Y = IP(c, P--(2*Q-P)); draw(A--B--C--A, black+0.8); draw(c^^X--Y^^B--Q^^C--P); dot("$A$", A, SW); dot("$B$", B, SE); dot("$C$", C, N); dot("$P$", P, SW); dot("$Q$", Q, W); dot("$X$", X, SE); dot("$Y$", Y, NW); label("$25$", P--Q, SW); label("$15$", Q--Y, SW); label("$10$", X--P, SW); [/asy]](http://latex.artofproblemsolving.com/0/b/9/0b96efb71a1d1aef4a0c2f0c402c8d9d0e29cee0.png)
Solution 1
First we have ![]() , and
, and ![]() by PoP. Similarly,
by PoP. Similarly, ![]() and dividing these each by
and dividing these each by ![]() gives
gives
![]() .
.
It is known that the sides of the orthic triangle are ![]() , and its angles are
, and its angles are ![]() ,
,![]() , and
, and ![]() . We thus have the three sides of the orthic triangle now.
Letting
. We thus have the three sides of the orthic triangle now.
Letting ![]() be the foot of the altitude from
be the foot of the altitude from ![]() , we have, in
, we have, in ![]() ,
,
![]()
![]() similarly, we get
similarly, we get
![]() To finish,
To finish, ![]() The requested sum is
The requested sum is ![]() .
.
༺\ crazyeyemoody9❂7 //༻
Solution 2
Let ![]() ,
, ![]() , and
, and ![]() . Let
. Let ![]() . Then
. Then ![]() and
and ![]() .
.
By Power of a Point theorem,
![]() Thus
Thus ![]() . Then
. Then ![]() ,
, ![]() , and
, and
![]() Use the Law of Cosines in
Use the Law of Cosines in ![]() to get
to get ![]() , which rearranges to
, which rearranges to ![]() Upon simplification, this reduces to a linear equation in
Upon simplification, this reduces to a linear equation in ![]() , with solution
, with solution ![]() . Then
. Then ![]() So the final answer is
So the final answer is ![]()
By SpecialBeing2017
Solution 3
Let ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . By Power of a Point,
. By Power of a Point,
![]() Points
Points ![]() and
and ![]() lie on the circle,
lie on the circle, ![]() , with diameter
, with diameter ![]() , and pow
, and pow![]() , so
, so ![]() Use Law of Cosines in
Use Law of Cosines in ![]() to get
to get ![]() ; since
; since ![]() , this simplifies as
, this simplifies as
![]() We get
We get ![]() and thus
and thus
![]() Therefore
Therefore ![]() . So the answer is
. So the answer is ![]()
By asr41
Solution 4 (Clean)
This solution is directly based of @CantonMathGuy's solution. We start off with a key claim.
Claim. ![]() and
and ![]() .
.
Proof.
Let ![]() and
and ![]() denote the reflections of the orthocenter over points
denote the reflections of the orthocenter over points ![]() and
and ![]() , respectively. Since
, respectively. Since ![]() and
and ![]() we have that
we have that ![]() is a rectangle. Then, since
is a rectangle. Then, since ![]() we obtain
we obtain ![]() (which directly follows from
(which directly follows from ![]() being cyclic); hence
being cyclic); hence ![]() , or
, or ![]() .
.
Similarly, we can obtain ![]() .
. ![]()
A direct result of this claim is that ![]() .
.
Thus, we can set ![]() and
and ![]() , then applying Power of a Point on
, then applying Power of a Point on ![]() we get
we get ![]() . Also, we can set
. Also, we can set ![]() and
and ![]() and once again applying Power of a Point (but this time to
and once again applying Power of a Point (but this time to ![]() ) we get
) we get
![]() .
.
Hence,
![]()
and the answer is ![]() . ~rocketsri
. ~rocketsri
See Also
| 2019 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()