Difference between revisions of "2020 AIME I Problems/Problem 6"
(→Solution 2 (Tangential distance)) |
MRENTHUSIASM (talk | contribs) (→Solution 2 (Tangential distance)) |
||
| Line 55: | Line 55: | ||
~molocyxu | ~molocyxu | ||
| − | ==Solution 2 (Tangential | + | ==Solution 2 (Tangential Distance)== |
[[File:2020 AIME I 6a.png|400px|right]] | [[File:2020 AIME I 6a.png|400px|right]] | ||
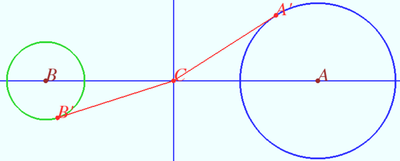
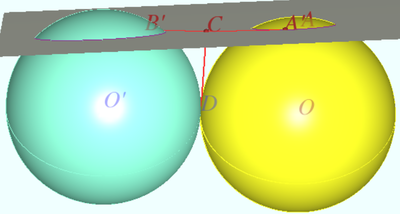
Let <math>A</math> and <math>B</math> be the centers of the holes, let <math>C</math> be the point of crossing <math>AB</math> and radical axes of the circles. So <math>C</math> has equal tangential distance to any point of both spheres. In particular to the circles (https://en.wikipedia.org/wiki/Radical_axis.) | Let <math>A</math> and <math>B</math> be the centers of the holes, let <math>C</math> be the point of crossing <math>AB</math> and radical axes of the circles. So <math>C</math> has equal tangential distance to any point of both spheres. In particular to the circles (https://en.wikipedia.org/wiki/Radical_axis.) | ||
Revision as of 01:07, 12 January 2023
Contents
Problem
A flat board has a circular hole with radius 
and a circular hole with radius 
such that the distance between the centers of the two holes is 
Two spheres with equal radii sit in the two holes such that the spheres are tangent to each other. The square of the radius of the spheres is 
where 
and 
are relatively prime positive integers. Find 
Solution
![[asy] size(10cm); pair A, B, C, D, O, P, H, L, X, Y; A = (-1, 0); B = (1, 0); H = (0, 0); C = (5, 0); D = (9, 0); L = (7, 0); O = (0, sqrt(160/13 - 1)); P = (7, sqrt(160/13 - 4)); X = (0, sqrt(160/13 - 4)); Y = (O + P) / 2; draw(A -- O -- B -- cycle); draw(C -- P -- D -- cycle); draw(B -- C); draw(O -- P); draw(P -- X, dashed); draw(O -- H, dashed); draw(P -- L, dashed); draw(circle(O, sqrt(160/13))); draw(circle(P, sqrt(160/13))); path b = brace(L-(0,1), H-(0,1),0.5); draw(b); label("$r$", O -- Y, N); label("$r$", Y -- P, N); label("$r$", O -- A, NW); label("$r$", P -- D, NE); label("$1$", A -- H, N); label("$2$", L -- D, N); label("$7$", b, S); dot(A^^B^^C^^D^^O^^P^^H^^L^^X^^Y,linewidth(4)); [/asy]](http://latex.artofproblemsolving.com/6/3/a/63af3ee78c8a31a2ef396006676d018ab50a0d2f.png)
Set the common radius to 
. First, take the cross section of the sphere sitting in the hole of radius . If we draw the perpendicular bisector of the chord (the hole) through the circle, this line goes through the center. Connect the center also to where the chord hits the circle, for a right triangle with hypotenuse and base . Therefore, the height of this circle outside of the hole is 
.
The other circle follows similarly for a height (outside the hole) of 
. Now, if we take the cross section of the entire board, essentially making it two-dimensional, we can connect the centers of the two spheres, then form another right triangle with base 
, as given by the problem. The height of this triangle is the difference between the heights of the parts of the two spheres outside the holes, which is 
. Now we can set up an equation in terms of with the Pythagorean theorem: ![\[\left(\sqrt{r^2-1} - \sqrt{r^2-4}\right)^2 + 7^2 = (2r)^2.\]](http://latex.artofproblemsolving.com/c/5/3/c5333012aea3a045a0d96d846d94552e32c9970f.png)
Simplifying a few times,
Therefore, our answer is 
.
~molocyxu
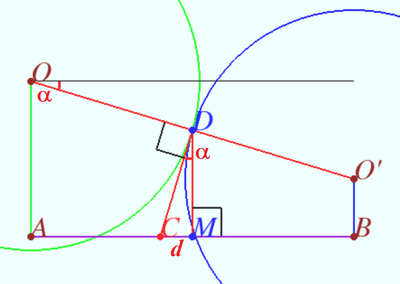
Solution 2 (Tangential Distance)
Let 
and 
be the centers of the holes, let 
be the point of crossing 
and radical axes of the circles. So has equal tangential distance to any point of both spheres. In particular to the circles (https://en.wikipedia.org/wiki/Radical_axis.)
![\[CA = \frac {AB} {2} – \frac {r_A^2 – r_B^2}{2 AB} = \frac{23}{7}, CB = AB - AC =\frac{26}{7},\]](http://latex.artofproblemsolving.com/a/0/2/a025b6d15152ebff4c98d5477dc438c4de6ac452.png)
![\[CA' = CB'= \sqrt{BC^2 – r_B^2} = \frac {4}{7} \sqrt{30}.\]](http://latex.artofproblemsolving.com/9/9/3/993874475cb03305ed2d842324e51b338cbf88cb.png)
Let 
be the point of tangency of the spheres common radius 
centered at 
and 
Let 
be the angle between 
and flat board. In the plane, perpendicular to board ![\[DC \perp OO', DC = \frac {4}{7} \sqrt{30}.\]](http://latex.artofproblemsolving.com/a/d/3/ad361428d6c5f4abbe1b74d7a1b7ec2bd0f7121e.png)
Distance between and midpoint 
of is
![\[d = \frac {26}{7} - \frac {7}{2} = \frac{3}{14} \implies \sin \alpha = \frac {d}{DC} = \frac {3}{8\sqrt 30}.\]](http://latex.artofproblemsolving.com/2/3/9/2399d7baf05068fb432c533b1a014674df509875.png)
![\[\cos \alpha = \sqrt {1 – \frac {9}{64 \cdot 30}} = \sqrt{ \frac {637}{640}} = \frac {7}{2} \sqrt {\frac{13}{160}}.\]](http://latex.artofproblemsolving.com/0/a/f/0af1c1835b358527f286f2f3d1956839c1a6878c.png)
![\[2R \cos \alpha = AB = 7 \implies R = \frac {\frac{7}{2} } {\frac{7}{2}\sqrt \frac{13}{160}} = \sqrt {\frac{160}{13}} .\]](http://latex.artofproblemsolving.com/6/e/9/6e9bfe01428bbc20b474eb54b2bc27a7f5112bbf.png)
vladimir.shelomovskii@gmail.com, vvsss
Video solution (With Animation)
Video Solution
https://www.youtube.com/watch?v=qCTq8KhZfYQ
See Also
| 2020 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 5 |
Followed by Problem 7 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
