Difference between revisions of "1997 AIME Problems/Problem 4"
m |
(sol) |
||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
| − | + | [[Circle]]s of [[radii]] <math>5, 5, 8,</math> and <math>\frac mn</math> are mutually externally tangent, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m + n.</math> | |
== Solution == | == Solution == | ||
| − | {{ | + | [[Image:1997_AIME-4.png]] |
| + | |||
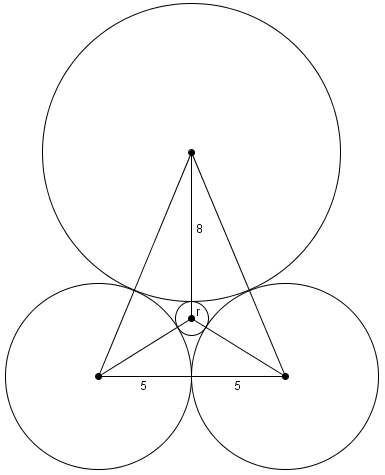
| + | If (in the diagram above) we draw the line going through the centers of the circles with radii <math>8</math> and <math>\frac mn = r</math>, that line is the perpendicular bisector of the segment connecting the centers of the two circles with radii <math>5</math>. Then we form two [[right triangles]], of lengths <math>5, x, 5+r</math> and <math>5, 8+r+x, 13</math>, wher <math>x</math> is the distance between the center of the circle in question and the segment connecting the centers of the two circles of radii <math>5</math>. By the [[Pythagorean Theorem]], we now have two equations with two unknowns: | ||
| + | |||
| + | <math>\begin{eqnarray*} | ||
| + | 5^2 + x^2 &=& (5+r)^2 \ | ||
| + | x &=& \sqrt{10r + r^2} \ | ||
| + | && \ | ||
| + | (8 + r + \sqrt{10r+r^2})^2 + 5^2 &=& 13^2\ | ||
| + | 8 + r + \sqrt{10r+r^2} &=& 12\ | ||
| + | \sqrt{10r+r^2}&=& 4-r\ | ||
| + | 10r+r^2 &=& 16 - 8r + r^2\ | ||
| + | r &=& \frac{8}{9} | ||
| + | \end{eqnarray*}</math> | ||
| + | |||
| + | So <math>m+n = \boxed{17}</math>. | ||
== See also == | == See also == | ||
{{AIME box|year=1997|num-b=3|num-a=5}} | {{AIME box|year=1997|num-b=3|num-a=5}} | ||
| + | |||
| + | [[Category:Intermediate Geometry Problems]] | ||
Revision as of 18:29, 21 November 2007
Problem
Circles of radii ![]() and
and ![]() are mutually externally tangent, where
are mutually externally tangent, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
Solution
If (in the diagram above) we draw the line going through the centers of the circles with radii ![]() and
and ![]() , that line is the perpendicular bisector of the segment connecting the centers of the two circles with radii
, that line is the perpendicular bisector of the segment connecting the centers of the two circles with radii ![]() . Then we form two right triangles, of lengths
. Then we form two right triangles, of lengths ![]() and
and ![]() , wher
, wher ![]() is the distance between the center of the circle in question and the segment connecting the centers of the two circles of radii
is the distance between the center of the circle in question and the segment connecting the centers of the two circles of radii ![]() . By the Pythagorean Theorem, we now have two equations with two unknowns:
. By the Pythagorean Theorem, we now have two equations with two unknowns:
$
So ![]() .
.
See also
| 1997 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 3 |
Followed by Problem 5 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||