Difference between revisions of "2021 AIME II Problems/Problem 12"
MRENTHUSIASM (talk | contribs) m (→Bretschneider's Formula) |
Mathkiddie (talk | contribs) (→Note 2) |
||
| (15 intermediate revisions by 7 users not shown) | |||
| Line 58: | Line 58: | ||
7^2 &= d^2 + a^2 - 2da\cos \theta. &&(4) | 7^2 &= d^2 + a^2 - 2da\cos \theta. &&(4) | ||
\end{align*}</cmath> | \end{align*}</cmath> | ||
| − | If we subtract <math>( | + | If we subtract <math>(2)+(4)</math> from <math>(1)+(3)</math>, the squared terms cancel, leaving us with: |
<cmath>\begin{align*} | <cmath>\begin{align*} | ||
5^2 + 9^2 - 6^2 - 7^2 &= 2ab \cos \theta + 2bc \cos \theta + 2cd \cos \theta + 2da \cos \theta \\ | 5^2 + 9^2 - 6^2 - 7^2 &= 2ab \cos \theta + 2bc \cos \theta + 2cd \cos \theta + 2da \cos \theta \\ | ||
| Line 156: | Line 156: | ||
~ Leo.Euler | ~ Leo.Euler | ||
| + | |||
| + | ==Solution 4 (Symmetry)== | ||
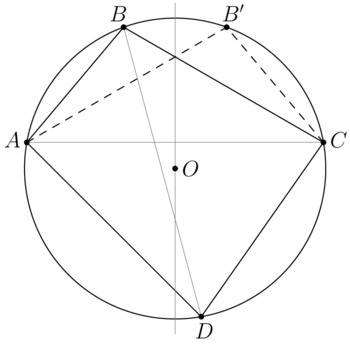
| + | [[File:AIME-I-2021-12.png|350px|right]] | ||
| + | <i><b>Claim</b></i> | ||
| + | |||
| + | Given an inscribed quadrilateral <math>ABCD</math> with sides <math>AB = a, BC = b, CD = c,</math> and <math>DA = d.</math> Prove that the <math>\angle \theta < 90^\circ</math> between the diagonals is given by | ||
| + | <cmath>\begin{align*}2(ac + bd) \cos \theta = {|d^2 – c^2 + b^2 – a^2|}.\end{align*}</cmath> | ||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Let the point <math>B'</math> be symmetric to <math>B</math> with respect to the perpendicular bisector <math>AC.</math> Then the quadrilateral <math>AB'CD</math> is an inscribed one, <math>AB' = b, B'C = a.</math> | ||
| + | |||
| + | <cmath> 2 \angle AEB = \overset{\Large\frown} {AB} + \overset{\Large\frown} {CD}.</cmath> | ||
| + | <cmath>\begin{align*} 2\angle B'AD = \overset{\Large\frown} {B'C} + \overset{\Large\frown} {CD} = \overset{\Large\frown} {AB} + \overset{\Large\frown} {CD} \implies \angle AEB = \angle B'AD.\end{align*}</cmath> | ||
| + | |||
| + | We apply the Law of Cosines to <math>\triangle AB'D</math> and <math>\triangle CB'D</math>: | ||
| + | <cmath>\begin{align*} B'D^2 = AD^2 + AB'^2 – 2 AD \cdot AB' \cos \theta, \end{align*}</cmath> | ||
| + | <cmath>\begin{align*} B'D^2 = CD^2 + CB'^2 + 2 CD \cdot CB' \cos \theta,\end{align*}</cmath> | ||
| + | <cmath>\begin{align*} d^2 + b^2 – 2 bd \cos \theta = c^2 + a^2 + 2ac \cos \theta,\end{align*}</cmath> | ||
| + | <cmath>\begin{align*} 2(ac + bd) \cos \theta = |d^2 – c^2 + b^2 – a^2|.\end{align*}</cmath> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Note 1== | ||
| + | By generalization, the tangent of the acute angle formed by the diagonals is <cmath>\left|\frac{4A}{a^2-b^2+c^2-d^2}\right|.</cmath> | ||
| + | |||
| + | ==Video Solution by MOP 2024== | ||
| + | https://youtu.be/K0u0ACMTSw8 | ||
| + | |||
| + | ~r00tsOfUnity | ||
==Video Solution== | ==Video Solution== | ||
https://www.youtube.com/watch?v=7DxIdTLNbo0 | https://www.youtube.com/watch?v=7DxIdTLNbo0 | ||
| + | |||
| + | ==Video Solution by Interstigation== | ||
| + | https://youtu.be/8GRO4za5rPI | ||
| + | |||
| + | ~Interstigation | ||
==See Also== | ==See Also== | ||
{{AIME box|year=2021|n=II|num-b=11|num-a=13}} | {{AIME box|year=2021|n=II|num-b=11|num-a=13}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Latest revision as of 16:33, 12 January 2024
Contents
Problem
A convex quadrilateral has area ![]() and side lengths
and side lengths ![]() and
and ![]() in that order. Denote by
in that order. Denote by ![]() the measure of the acute angle formed by the diagonals of the quadrilateral. Then
the measure of the acute angle formed by the diagonals of the quadrilateral. Then ![]() can be written in the form
can be written in the form ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Solution 1 (Sines and Cosines)
Since we are asked to find ![]() , we can find
, we can find ![]() and
and ![]() separately and use their values to get
separately and use their values to get ![]() . We can start by drawing a diagram. Let the vertices of the quadrilateral be
. We can start by drawing a diagram. Let the vertices of the quadrilateral be ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Let
. Let ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Let
. Let ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . We know that
. We know that ![]() is the acute angle formed between the intersection of the diagonals
is the acute angle formed between the intersection of the diagonals ![]() and
and ![]() .
.
![[asy] unitsize(4cm); pair A,B,C,D,X; A = (0,0); B = (1,0); C = (1.25,-1); D = (-0.75,-0.75); draw(A--B--C--D--cycle,black+1bp); X = intersectionpoint(A--C,B--D); draw(A--C); draw(B--D); label("$A$",A,NW); label("$B$",B,NE); label("$C$",C,SE); label("$D$",D,SW); dot(X); label("$X$",X,S); label("$5$",(A+B)/2,N); label("$6$",(B+C)/2,E); label("$9$",(C+D)/2,S); label("$7$",(D+A)/2,W); label("$\theta$",X,2.5E); label("$a$",(A+X)/2,NE); label("$b$",(B+X)/2,NW); label("$c$",(C+X)/2,SW); label("$d$",(D+X)/2,SE); [/asy]](http://latex.artofproblemsolving.com/0/c/8/0c8fe8bfd35bddd29e1d986195ef4801b7bc8e63.png) We are given that the area of quadrilateral
We are given that the area of quadrilateral ![]() is
is ![]() . We can express this area using the areas of triangles
. We can express this area using the areas of triangles ![]() ,
, ![]() ,
, ![]() , and
, and ![]() . Since we want to find
. Since we want to find ![]() and
and ![]() , we can represent these areas using
, we can represent these areas using ![]() as follows:
as follows:
![\begin{align*} 30 &=[ABCD] \\ &=[AXB] + [BXC] + [CXD] + [DXA] \\ &=\frac{1}{2} ab \sin (\angle AXB) + \frac{1}{2} bc \sin (\angle BXC) + \frac{1}{2} cd \sin (\angle CXD) + \frac{1}{2} da \sin (\angle AXD) \\ &=\frac{1}{2} ab \sin (180^\circ - \theta) + \frac{1}{2} bc \sin (\theta) + \frac{1}{2} cd \sin (180^\circ - \theta) + \frac{1}{2} da \sin (\theta). \end{align*}](http://latex.artofproblemsolving.com/7/0/6/706452485c6b6cec38a2ad349109e199044c6395.png) We know that
We know that ![]() . Therefore it follows that:
. Therefore it follows that:
 From here we see that
From here we see that ![]() . Now we need to find
. Now we need to find ![]() . Using the Law of Cosines on each of the four smaller triangles, we get following equations:
. Using the Law of Cosines on each of the four smaller triangles, we get following equations:
 We know that
We know that ![]() for all
for all ![]() . We can substitute this value into our equations to get:
. We can substitute this value into our equations to get:
 If we subtract
If we subtract ![]() from
from ![]() , the squared terms cancel, leaving us with:
, the squared terms cancel, leaving us with:
![]() From here we see that
From here we see that ![]() .
.
Since we have figured out ![]() and
and ![]() , we can calculate
, we can calculate ![]() :
: ![\[\tan \theta = \frac{\sin \theta}{\cos \theta} = \frac{\frac{60}{ab + bc + cd + da}}{\frac{21/2}{ab + bc + cd + da}} = \frac{60}{21/2} = \frac{120}{21} = \frac{40}{7}.\]](http://latex.artofproblemsolving.com/5/0/9/509d3858cb3bed38db134b26f63a7d0fea216fe6.png) Therefore our answer is
Therefore our answer is ![]() .
.
~ Steven Chen (www.professorchenedu.com)
~ my_aops_lessons
Solution 2 (Right Triangles)
In convex quadrilateral ![]() let
let ![]() and
and ![]() Let
Let ![]() and
and ![]() be the feet of the perpendiculars from
be the feet of the perpendiculars from ![]() and
and ![]() respectively, to
respectively, to ![]() We obtain the following diagram:
We obtain the following diagram:
![[asy] /* Made by MRENTHUSIASM */ size(500); pair A, B, C, D, P, A1, C1; B = origin; D = (3*sqrt(32498*(29400*sqrt(47)+312523))/32498,0); A = intersectionpoints(Circle(B,5),Circle(D,7))[0]; C = intersectionpoints(Circle(B,6),Circle(D,9))[1]; P = intersectionpoint(A--C,B--D); A1 = foot(A,B,D); C1 = foot(C,B,D); markscalefactor=3/160; draw(rightanglemark(A,A1,D),red); draw(rightanglemark(C,C1,B),red); dot("$A$",A,1.5*dir(aCos(7/sqrt(1649)))); dot("$B$",B,1.5*W); dot("$C$",C,1.5*dir(180+aCos(7/sqrt(1649)))); dot("$D$",D,1.5*E); dot("$E$",P,dir(180-(180-aCos(7/sqrt(1649)))/2)); dot("$A'$",A1,dir(-75)); dot("$C'$",C1,N); label("$\theta$",P,dir(180+aCos(7/sqrt(1649))/2),red); draw(A--A1^^C--C1,dashed); draw(A--B--C--D--cycle^^A--C^^B--D); [/asy]](http://latex.artofproblemsolving.com/e/a/a/eaad14a17c0f6c7a078d77fa4c6788e26b9409ae.png) Let
Let ![]() and
and ![]() We apply the Pythagorean Theorem to right triangles
We apply the Pythagorean Theorem to right triangles ![]() and
and ![]() respectively:
respectively:
![\[\begin{array}{ccccccccccccccccc} (p+q+r)^2&+&h_1^2&=&5^2, &&&&&&&&&&&&\hspace{36mm}(1) \\ [1ex] p^2&+&h_2^2&=&6^2, &&&&&&&&&&&&\hspace{36mm}(2) \\ [1ex] (q+r+s)^2&+&h_2^2&=&9^2, &&&&&&&&&&&&\hspace{36mm}(3) \\ [1ex] s^2&+&h_1^2&=&7^2. &&&&&&&&&&&&\hspace{36mm}(4) \end{array}\]](http://latex.artofproblemsolving.com/6/d/8/6d892a581db85152efa92115ea6c35bd32724782.png) Let the brackets denote areas. We get
Let the brackets denote areas. We get
![\begin{align*} [ABD]+[CBD]&=[ABCD] \\ \frac12(p+q+r+s)h_1+\frac12(p+q+r+s)h_2&=30 \\ \frac12(p+q+r+s)(h_1+h_2)&=30 \\ (p+q+r+s)(h_1+h_2)&=60. \hspace{49.25mm}(5) \end{align*}](http://latex.artofproblemsolving.com/f/c/d/fcdc2189cf8d7c3f2c93ec59190361210f7a14d0.png) We subtract
We subtract ![]() from
from ![]()
![\begin{align*} (p+q+r)^2+(q+r+s)^2-p^2-s^2&=21 \\ \left[(p+q+r)^2-s^2\right]+\left[(q+r+s)^2-p^2\right]&=21 \\ (p+q+r+s)(p+q+r-s)+(p+q+r+s)(-p+q+r+s)&=21 \\ (p+q+r+s)(2q+2r)&=21 \\ 2(p+q+r+s)(q+r)&=21 \\ (p+q+r+s)(q+r)&=\frac{21}{2}. \hspace{9.5mm}(6) \end{align*}](http://latex.artofproblemsolving.com/3/3/f/33f3edc91bb17b51407e22eded41aa32c7ade23f.png) From right triangles
From right triangles ![]() and
and ![]() we have
we have ![]() It follows that
It follows that
 Finally, we divide
Finally, we divide ![]() by
by ![]()
 from which the answer is
from which the answer is ![]()
~MRENTHUSIASM
Solution 3 (Bretschneider's Formula)
Bretschneider's Formula
![[asy] size(200); import olympiad; defaultpen(linewidth(0.8)+fontsize(10)); pair A,B,C,D; A=origin; B=(1.25,0); D=dir(65); C=D+0.85*dir(90)*(A-D); draw(A--B--C--D--cycle); draw(A--C^^B--D, gray+0.5); dot("$A$", A, SW); dot("$B$", B, SE); dot("$C$", C, NE); dot("$D$",D,NW); label("$a$", A--B, S); label("$b$", B--C, E); label("$c$", D--C, N); label("$d$",D--A,W); label("$u$",D--B,2*dir(170)); label("$v$",A--C,S); [/asy]](http://latex.artofproblemsolving.com/2/3/0/230b3c79642cd579ca59e6d44347e92acedc4b0a.png) Given quadrilateral
Given quadrilateral ![]() , let,
, let, ![]() , be the sides,
, be the sides, ![]() the semiperimeter, and
the semiperimeter, and ![]() , the diagonals. Then the area,
, the diagonals. Then the area, ![]() , is given by
, is given by ![]()
Solution
By Bretschneider's Formula, ![]() Thus,
Thus, ![]() . Also,
. Also, ![]() solving for
solving for ![]() yields
yields ![]() . Since
. Since ![]() is acute,
is acute, ![]() is positive, from which
is positive, from which ![]() . Solving for
. Solving for ![]() yields
yields ![]() for a final answer of
for a final answer of ![]() .
.
~ Leo.Euler
Solution 4 (Symmetry)
Claim
Given an inscribed quadrilateral ![]() with sides
with sides ![]() and
and ![]() Prove that the
Prove that the ![]() between the diagonals is given by
between the diagonals is given by
![]() Proof
Proof
Let the point ![]() be symmetric to
be symmetric to ![]() with respect to the perpendicular bisector
with respect to the perpendicular bisector ![]() Then the quadrilateral
Then the quadrilateral ![]() is an inscribed one,
is an inscribed one, ![]()
![]()
![]()
We apply the Law of Cosines to ![]() and
and ![]() :
:
![]()
![]()
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
Note 1
By generalization, the tangent of the acute angle formed by the diagonals is ![]()
Video Solution by MOP 2024
~r00tsOfUnity
Video Solution
https://www.youtube.com/watch?v=7DxIdTLNbo0
Video Solution by Interstigation
~Interstigation
See Also
| 2021 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 11 |
Followed by Problem 13 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.