Difference between revisions of "2018 AIME II Problems/Problem 14"
(→Solution 2 (Projective)) |
(→Solution 4 (Projective geometry)) |
||
| (16 intermediate revisions by 7 users not shown) | |||
| Line 3: | Line 3: | ||
The incircle <math>\omega</math> of triangle <math>ABC</math> is tangent to <math>\overline{BC}</math> at <math>X</math>. Let <math>Y \neq X</math> be the other intersection of <math>\overline{AX}</math> with <math>\omega</math>. Points <math>P</math> and <math>Q</math> lie on <math>\overline{AB}</math> and <math>\overline{AC}</math>, respectively, so that <math>\overline{PQ}</math> is tangent to <math>\omega</math> at <math>Y</math>. Assume that <math>AP = 3</math>, <math>PB = 4</math>, <math>AC = 8</math>, and <math>AQ = \dfrac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>. | The incircle <math>\omega</math> of triangle <math>ABC</math> is tangent to <math>\overline{BC}</math> at <math>X</math>. Let <math>Y \neq X</math> be the other intersection of <math>\overline{AX}</math> with <math>\omega</math>. Points <math>P</math> and <math>Q</math> lie on <math>\overline{AB}</math> and <math>\overline{AC}</math>, respectively, so that <math>\overline{PQ}</math> is tangent to <math>\omega</math> at <math>Y</math>. Assume that <math>AP = 3</math>, <math>PB = 4</math>, <math>AC = 8</math>, and <math>AQ = \dfrac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>. | ||
| + | |||
| + | ==Diagram== | ||
| + | <asy> size(200); import olympiad; defaultpen(linewidth(1)+fontsize(12)); | ||
| + | pair A,B,C,P,Q,Wp,X,Y,Z; B=origin; C=(6.75,0); A=IP(CR(B,7),CR(C,8)); path c=incircle(A,B,C); Wp=IP(c,A--C); Z=IP(c,A--B); X=IP(c,B--C); Y=IP(c,A--X); pair I=incenter(A,B,C); P=extension(A,B,Y,Y+dir(90)*(Y-I)); Q=extension(A,C,P,Y); | ||
| + | draw(A--B--C--cycle, black+1); draw(c^^A--X^^P--Q); | ||
| + | pen p=4+black; dot("$A$",A,N,p); dot("$B$",B,SW,p); dot("$C$",C,SE,p); dot("$X$",X,S,p); dot("$Y$",Y,dir(55),p); dot("$W$",Wp,E,p); dot("$Z$",Z,W,p); dot("$P$",P,W,p); dot("$Q$",Q,E,p); MA("\beta",C,X,A,0.3,black); MA("\alpha",B,A,X,0.7,black); </asy> | ||
==Solution 1== | ==Solution 1== | ||
| Line 8: | Line 14: | ||
==Solution 2 (Projective)== | ==Solution 2 (Projective)== | ||
| − | Let the incircle of <math>ABC</math> be tangent to <math>AB</math> and <math>AC</math> at <math> | + | Let the incircle of <math>ABC</math> be tangent to <math>AB</math> and <math>AC</math> at <math>Z</math> and <math>W</math>. By Brianchon's theorem on tangential hexagons <math>QWCBZP</math> and <math>PYQCXB</math>, we know that <math>ZW,CP,BQ</math> and <math>XY</math> are concurrent at a point <math>O</math>. Let <math>PQ \cap BC = M</math>. Then by La Hire's <math>A</math> lies on the polar of <math>M</math> so <math>M</math> lies on the polar of <math>A</math>. Therefore, <math>ZW</math> also passes through <math>M</math>. Then projecting through <math>M</math>, we have |
| − | <cmath> -1 = (A,O;Y,X) \stackrel{ | + | <cmath> -1 = (A,O;Y,X) \stackrel{M}{=} (A,Z;P,B) \stackrel{M}{=} (A,W;Q,C).</cmath>Therefore, <math>\frac{AP \cdot ZB}{MP \cdot AB} = 1 \implies \frac{3 \cdot ZB}{ZP \cdot 7} = 1</math>. Since <math>ZB+ZP=4</math> we know that <math>ZP = \frac{6}{5}</math> and <math>ZB = \frac{14}{5}</math>. Therefore, <math>AW = AZ = \frac{21}{5}</math> and <math>WC = 8 - \frac{21}{5} = \frac{19}{5}</math>. Since <math>(A,W;Q,C) = -1</math>, we also have <math>\frac{AQ \cdot WC}{NQ \cdot AC} = 1 \implies \frac{AQ \cdot \tfrac{19}{5}}{(\tfrac{21}{5} - AQ) \cdot 8} = 1</math>. Solving for <math>AQ</math>, we obtain <math>AQ = \frac{168}{59} \implies m+n = \boxed{227}</math>. |
| − | + | 😃 | |
-Vfire | -Vfire | ||
| Line 63: | Line 69: | ||
~Solution by <math>BladeRunnerAUG</math> (Frank FYC) | ~Solution by <math>BladeRunnerAUG</math> (Frank FYC) | ||
| + | |||
| + | ==Solution 4 (Projective geometry)== | ||
| + | [[File:2018 AIME II 14.png|500px|right]] | ||
| + | <i><b>Claim</b></i> | ||
| + | |||
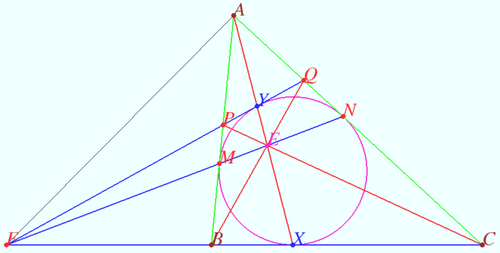
| + | Let the sides <math>\overline{AB}</math> and <math>\overline{AC}</math> be tangent to <math>\omega</math> at <math>M</math> and <math>N</math>, respectively. Then | ||
| + | lines <math>PQ, MN,</math> and <math>BC</math> are concurrent and lines <math>PC, MN, AX,</math> and <math>BQ</math> are concurrent. | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Let <math>E</math> be point of crossing <math>AX</math> and <math>BQ.</math> We make projective transformation such that circle <math>\omega</math> maps into the circle and point <math>E</math> maps into the center of new circle point <math>I.</math> We denote images using notification <math>X \rightarrow X'.</math> | ||
| + | [[File:2018 AIME II 14a.png|300px|right]] | ||
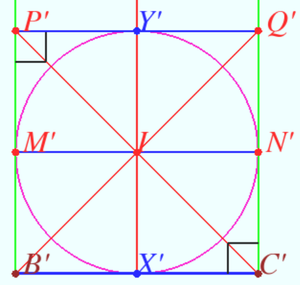
| + | <math>BCQP</math> maps into <math>B'C'Q'P'</math>, so lines <math>B'Q'</math> and <math>A'X'</math> be the diameters. | ||
| + | This implies <math>P'Q'||B'C', \angle B'P'Q' = \angle B'C'Q' = 90^\circ \implies B'C'Q'P'</math> be a square. | ||
| + | |||
| + | Therefore <math>M'N'</math> be the diameter <math>\implies P'C', B'Q',</math> be diagonals of the square. <math>M'N'</math> and <math>X'Y'</math> be midlines which crossing in the center <math>I.</math> Therefore lines <math>PC, MN, AX,</math> and <math>BQ</math> are concurrent. | ||
| + | |||
| + | Lines <math>P'Q'||M'N' ||B'C' \implies PQ, MN</math> and <math>BC</math> are concurrent. | ||
| + | |||
| + | <i><b>Solution</b></i> | ||
| + | The cross-ratio associated with a list of four collinear points <math>A,P,M,D</math> is defined as <cmath>(A,P;M,B)={\frac {AP\cdot MB}{AB\cdot PM}}.</cmath> | ||
| + | The cross-ratio be <i><b>projective invariant</b></i> of a quadruple of collinear points, so | ||
| + | [[File:2018 AIME II 14b.png|300px|right]] | ||
| + | <cmath>(A,P; M,B) = {\frac {A'P'\cdot M'B'}{A'B'\cdot P'M'}} = \frac {M'B'}{P'M'} = 1.</cmath> | ||
| + | <cmath>(A,P; M,B)={\frac {3\cdot (7 - AM)}{7\cdot (AM - 3)}} = 1 \implies AM = \frac {21}{5} \implies AN = AM = \frac {21}{5}.</cmath> | ||
| + | [[File:2018 AIME II 14c.png|300px|right]] | ||
| + | <cmath>(A,Q;N,C)={\frac {AQ\cdot NC}{AC\cdot QN}} = \frac {AQ\cdot (AC- AN)}{AC\cdot (AN-AQ)} = 1.</cmath> | ||
| + | <cmath>AQ \cdot (8 - \frac{21}{5}) = 8 \cdot (\frac{21}{5} – AQ) \implies AQ = \frac{168}{59}.</cmath> | ||
| + | |||
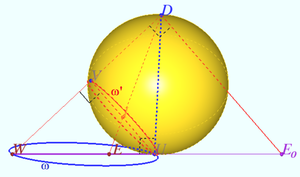
| + | For visuals only, I will show how one can find the perceptor <math>D</math> and the image’s plane. | ||
| + | <math>E_0</math> is image of inversion <math>E</math> with respect <math>\omega.</math> | ||
| + | <math>UW</math> is the diameter of <math>\omega, E,E_0,U,W</math> are collinear. | ||
| + | <math>DU \perp \omega, DE_0\perp WD, UV \perp WD, UV</math> is diameter of <math>\omega'</math>. | ||
| + | |||
| + | Plane of images is perpendicular to <math>WD.</math> | ||
| + | |||
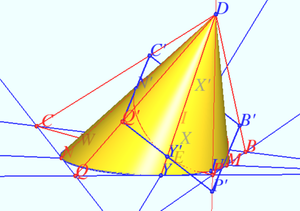
| + | Last diagram shows the result of transformation. Transformation is possible. The end. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Video Solution by Mop 2024== | ||
| + | https://youtu.be/SIs1JFLFzyw | ||
| + | |||
| + | ~r00tsOfUnity | ||
| + | |||
| + | ==See Also== | ||
{{AIME box|year=2018|n=II|num-b=13|num-a=15}} | {{AIME box|year=2018|n=II|num-b=13|num-a=15}} | ||
| + | |||
| + | [[Category:Intermediate Geometry Problems]] | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Revision as of 13:32, 28 January 2024
Contents
Problem
The incircle ![]() of triangle
of triangle ![]() is tangent to
is tangent to ![]() at
at ![]() . Let
. Let ![]() be the other intersection of
be the other intersection of ![]() with
with ![]() . Points
. Points ![]() and
and ![]() lie on
lie on ![]() and
and ![]() , respectively, so that
, respectively, so that ![]() is tangent to
is tangent to ![]() at
at ![]() . Assume that
. Assume that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Diagram
![[asy] size(200); import olympiad; defaultpen(linewidth(1)+fontsize(12)); pair A,B,C,P,Q,Wp,X,Y,Z; B=origin; C=(6.75,0); A=IP(CR(B,7),CR(C,8)); path c=incircle(A,B,C); Wp=IP(c,A--C); Z=IP(c,A--B); X=IP(c,B--C); Y=IP(c,A--X); pair I=incenter(A,B,C); P=extension(A,B,Y,Y+dir(90)*(Y-I)); Q=extension(A,C,P,Y); draw(A--B--C--cycle, black+1); draw(c^^A--X^^P--Q); pen p=4+black; dot("$A$",A,N,p); dot("$B$",B,SW,p); dot("$C$",C,SE,p); dot("$X$",X,S,p); dot("$Y$",Y,dir(55),p); dot("$W$",Wp,E,p); dot("$Z$",Z,W,p); dot("$P$",P,W,p); dot("$Q$",Q,E,p); MA("\beta",C,X,A,0.3,black); MA("\alpha",B,A,X,0.7,black); [/asy]](http://latex.artofproblemsolving.com/4/0/7/4073dcacb93163e2fca4cd2a02d09ff864a1f50b.png)
Solution 1
Let the sides ![]() and
and ![]() be tangent to
be tangent to ![]() at
at ![]() and
and ![]() , respectively. Let
, respectively. Let ![]() and
and ![]() . Because
. Because ![]() and
and ![]() are both tangent to
are both tangent to ![]() and
and ![]() and
and ![]() subtend the same arc of
subtend the same arc of ![]() , it follows that
, it follows that ![]() . By equal tangents,
. By equal tangents, ![]() . Applying the Law of Sines to
. Applying the Law of Sines to ![]() yields
yields ![]() Similarly, applying the Law of Sines to
Similarly, applying the Law of Sines to ![]() gives
gives ![]() It follows that
It follows that ![]() implying
implying ![]() . Applying the same argument to
. Applying the same argument to ![]() yields
yields ![]() from which
from which ![]() . The requested sum is
. The requested sum is ![]() .
.
Solution 2 (Projective)
Let the incircle of ![]() be tangent to
be tangent to ![]() and
and ![]() at
at ![]() and
and ![]() . By Brianchon's theorem on tangential hexagons
. By Brianchon's theorem on tangential hexagons ![]() and
and ![]() , we know that
, we know that ![]() and
and ![]() are concurrent at a point
are concurrent at a point ![]() . Let
. Let ![]() . Then by La Hire's
. Then by La Hire's ![]() lies on the polar of
lies on the polar of ![]() so
so ![]() lies on the polar of
lies on the polar of ![]() . Therefore,
. Therefore, ![]() also passes through
also passes through ![]() . Then projecting through
. Then projecting through ![]() , we have
, we have
![]() Therefore,
Therefore, ![]() . Since
. Since ![]() we know that
we know that ![]() and
and ![]() . Therefore,
. Therefore, ![]() and
and ![]() . Since
. Since ![]() , we also have
, we also have ![]() . Solving for
. Solving for ![]() , we obtain
, we obtain ![]() .
😃
-Vfire
.
😃
-Vfire
Solution 3 (Combination of Law of Sine and Law of Cosine)
Let the center of the incircle of ![]() be
be ![]() . Link
. Link ![]() and
and ![]() . Then we have
. Then we have ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Let the incircle of ![]() be tangent to
be tangent to ![]() and
and ![]() at
at ![]() and
and ![]() , let
, let ![]() and
and ![]() .
.
Use Law of Sine in ![]() and
and ![]() , we have
, we have
![]()
![]()
therefore we have
![]()
Solve this equation, we have ![]()
As a result, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
So, ![]()
Use Law of Cosine in ![]() and
and ![]() , we have
, we have
![]()

And we have
![]()
So

Solve this equation, we have ![]()
As a result, ![]()
So, the final answer of this question is ![]()
~Solution by ![]() (Frank FYC)
(Frank FYC)
Solution 4 (Projective geometry)
Claim
Let the sides ![]() and
and ![]() be tangent to
be tangent to ![]() at
at ![]() and
and ![]() , respectively. Then
lines
, respectively. Then
lines ![]() and
and ![]() are concurrent and lines
are concurrent and lines ![]() and
and ![]() are concurrent.
are concurrent.
Proof
Let ![]() be point of crossing
be point of crossing ![]() and
and ![]() We make projective transformation such that circle
We make projective transformation such that circle ![]() maps into the circle and point
maps into the circle and point ![]() maps into the center of new circle point
maps into the center of new circle point ![]() We denote images using notification
We denote images using notification ![]()
![]() maps into
maps into ![]() , so lines
, so lines ![]() and
and ![]() be the diameters.
This implies
be the diameters.
This implies ![]() be a square.
be a square.
Therefore ![]() be the diameter
be the diameter ![]() be diagonals of the square.
be diagonals of the square. ![]() and
and ![]() be midlines which crossing in the center
be midlines which crossing in the center ![]() Therefore lines
Therefore lines ![]() and
and ![]() are concurrent.
are concurrent.
Lines ![]() and
and ![]() are concurrent.
are concurrent.
Solution
The cross-ratio associated with a list of four collinear points ![]() is defined as
is defined as ![]() The cross-ratio be projective invariant of a quadruple of collinear points, so
The cross-ratio be projective invariant of a quadruple of collinear points, so
![]()
![]()
![]()
![]()
For visuals only, I will show how one can find the perceptor ![]() and the image’s plane.
and the image’s plane.
![]() is image of inversion
is image of inversion ![]() with respect
with respect ![]()
![]() is the diameter of
is the diameter of ![]() are collinear.
are collinear.
![]() is diameter of
is diameter of ![]() .
.
Plane of images is perpendicular to ![]()
Last diagram shows the result of transformation. Transformation is possible. The end.
vladimir.shelomovskii@gmail.com, vvsss
Video Solution by Mop 2024
~r00tsOfUnity
See Also
| 2018 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 13 |
Followed by Problem 15 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()