Difference between revisions of "2022 AIME II Problems/Problem 11"

Latest revision as of 17:26, 8 February 2024

Problem

Let $ABCD$ be a convex quadrilateral with $AB=2, AD=7,$ and $CD=3$ such that the bisectors of acute angles $\angle{DAB}$ and $\angle{ADC}$ intersect at the midpoint of $\overline{BC}.$ Find the square of the area of $ABCD.$

Solution 1

$[asy] defaultpen(fontsize(12)+0.6); size(300); pair A,B,C,D,M,H; real xb=71, xd=121; A=origin; D=(7,0); B=2*dir(xb); C=3*dir(xd)+D; M=(B+C)/2; H=foot(M,A,D); path c=CR(D,3); pair A1=bisectorpoint(D,A,B), D1=bisectorpoint(C,D,A), Bp=IP(CR(A,2),A--H), Cp=IP(CR(D,3),D--H); draw(B--A--D--C--B); draw(A--M--D^^M--H^^Bp--M--Cp, gray+0.4); draw(rightanglemark(A,H,M,5)); dot("$A$",A,SW); dot("$D$",D,SE); dot("$B$",B,NW); dot("$C$",C,NE); dot("$M$",M,up); dot("$H$",H,down); dot("$B'$",Bp,down); dot("$C'$",Cp,down); [/asy]$

According to the problem, we have $AB=AB'=2$ , $DC=DC'=3$ , $MB=MB'$ , $MC=MC'$ , and $B'C'=7-2-3=2$

Because $M$ is the midpoint of $BC$ , we have $BM=MC$ , so: $MB=MB'=MC'=MC.$

Then, we can see that $\bigtriangleup{MB'C'}$ is an isosceles triangle with $MB'=MC'$

Therefore, we could start our angle chasing: $\angle{MB'C'}=\angle{MC'B'}=180^\circ-\angle{MC'D}=180^\circ-\angle{MCD}$ .

This is when we found that points $M$ , $C$ , $D$ , and $B'$ are on a circle. Thus, $\angle{BMB'}=\angle{CDC'} \Rightarrow \angle{B'MA}=\angle{C'DM}$ . This is the time we found that $\bigtriangleup{AB'M} \sim \bigtriangleup{MC'D}$ .

Thus, $\frac{AB'}{B'M}=\frac{MC'}{C'D} \Longrightarrow (B'M)^2=AB' \cdot C'D = 6$

Point $H$ is the midpoint of $B'C'$ , and $MH \perp AD$ . $B'H=HC'=1 \Longrightarrow MH=\sqrt{B'M^2-B'H^2}=\sqrt{6-1}=\sqrt{5}$ .

The area of this quadrilateral is the sum of areas of triangles: $S_{\bigtriangleup{ABM}}+S_{\bigtriangleup{AB'M}}+S_{\bigtriangleup{CDM}}+S_{\bigtriangleup{CD'M}}+S_{\bigtriangleup{B'C'M}}$ $=S_{\bigtriangleup{AB'M}}\cdot 2 + S_{\bigtriangleup{B'C'M}} + S_{\bigtriangleup{C'DM}}\cdot 2$ $=2 \cdot \frac{1}{2} \cdot AB' \cdot MH + \frac{1}{2} \cdot B'C' \cdot MH + 2 \cdot \frac{1}{2} \cdot C'D \cdot MH$ $=2\sqrt{5}+\sqrt{5}+3\sqrt{5}=6\sqrt{5}$

Finally, the square of the area is $(6\sqrt{5})^2=\boxed{180}$

Solution 2

Denote by $M$ the midpoint of segment $BC$ . Let points $P$ and $Q$ be on segment $AD$ , such that $AP = AB$ and $DQ = DC$ .

Denote $\angle DAM = \alpha$ , $\angle BAD = \beta$ , $\angle BMA = \theta$ , $\angle CMD = \phi$ .

Denote $BM = x$ . Because $M$ is the midpoint of $BC$ , $CM = x$ .

Because $AM$ is the angle bisector of $\angle BAD$ and $AB = AP$ , $\triangle BAM \cong \triangle PAM$ . Hence, $MP = MB$ and $\angle AMP = \theta$ . Hence, $\angle MPD = \angle MAP + \angle PMA = \alpha + \theta$ .

Because $DM$ is the angle bisector of $\angle CDA$ and $DC = DQ$ , $\triangle CDM \cong \triangle QDM$ . Hence, $MQ = MC$ and $\angle DMQ = \phi$ . Hence, $\angle MQA = \angle MDQ + \angle QMD = \beta + \phi$ .

Because $M$ is the midpoint of segment $BC$ , $MB = MC$ . Because $MP = MB$ and $MQ = MC$ , $MP = MQ$ .

Thus, $\angle MPD = \angle MQA$ .

Thus, $\alpha + \theta = \beta + \phi . \hspace{1cm} (1)$

In $\triangle AMD$ , $\angle AMD = 180^\circ - \angle MAD - \angle MDA = 180^\circ - \alpha - \beta$ . In addition, $\angle AMD = 180^\circ - \angle BMA - \angle CMD = 180^\circ - \theta - \phi$ . Thus, $\alpha + \beta = \theta + \phi . \hspace{1cm} (2)$

Taking $(1) + (2)$ , we get $\alpha = \phi$ . Taking $(1) - (2)$ , we get $\beta = \theta$ .

Therefore, $\triangle ADM \sim \triangle AMB \sim \triangle MDC$ .

Hence, $\frac{AD}{AM} = \frac{AM}{AB}$ and $\frac{AD}{DM} = \frac{DM}{CD}$ . Thus, $AM = \sqrt{AD \cdot AD} = \sqrt{14}$ and $DM = \sqrt{AD \cdot CD} = \sqrt{21}$ .

In $\triangle ADM$ , by applying the law of cosines, $\cos \angle AMD = \frac{AM^2 + DM^2 - AD^2}{2 AM \cdot DM} = - \frac{1}{\sqrt{6}}$ . Hence, $\sin \angle AMD = \sqrt{1 - \cos^2 \angle AMD} = \frac{\sqrt{5}}{\sqrt{6}}$ . Hence, ${\rm Area} \ \triangle ADM = \frac{1}{2} AM \cdot DM \dot \sin \angle AMD = \frac{7 \sqrt{5}}{2}$ .

Therefore, $\begin{align*} {\rm Area} \ ABCD & = {\rm Area} \ \triangle AMD + {\rm Area} \ \triangle ABM + {\rm Area} \ \triangle MCD \\ & = {\rm Area} \ \triangle AMD \left( 1 + \left( \frac{AM}{AD} \right)^2 + \left( \frac{MD}{AD} \right)^2 \right) \\ & = 6 \sqrt{5} . \end{align*}$

Therefore, the square of ${\rm Area} \ ABCD$ is $\left( 6 \sqrt{5} \right)^2 = \boxed{\textbf{(180) }}$ .

~Steven Chen (www.professorchenedu.com)

Solution 3 (Visual)

Claim

In the triangle $ABC, AB = 2AC, M$ is the midpoint of $AB. D$ is the point of intersection of the circumcircle and the bisector of angle $A.$ Then $DM = BD.$

Proof

Let $A = 2\alpha.$ Then $\angle DBC = \angle DCB = \alpha.$

Let $E$ be the intersection point of the perpendicular dropped from $D$ to $AB$ with the circle.

Then the sum of arcs $\overset{\Large\frown} {BE} + \overset{\Large\frown}{AC} + \overset{\Large\frown}{CD} = 180^\circ.$ $\overset{\Large\frown} {BE} = 180^\circ – 2\alpha – \overset{\Large\frown}{AC}.$

Let $E'$ be the point of intersection of the line $CM$ with the circle. $CM$ is perpendicular to $AD, \angle AMC = 90^\circ – \alpha,$ the sum of arcs $\overset{\Large\frown}{A}C + \overset{\Large\frown}{BE'} = 180^\circ – 2\alpha \implies E'$ coincides with $E.$

The inscribed angles $\angle DEM = \angle DEB, M$ is symmetric to $B$ with respect to $DE, DM = DB.$

Solution

Let $AB' = AB, DC' = DC, B'$ and $C'$ on $AD.$

Then $AB' = 2, DC' = 3, B'C' = 2 = AB'.$

Quadrilateral $ABMC'$ is cyclic. Let $\angle A = 2\alpha.$ Then $\angle MBC' = \angle MC'B = \alpha.$

Circle $BB'C'C$ centered at $M, BC$ is its diameter, $\angle BC'C = 90^\circ.$ $\angle DMC' = \angle MC'B,$ since they both complete $\angle MC'C$ to $90^\circ.$

$\angle MB'A = \angle MC'D,$ since they are the exterior angles of an isosceles $\triangle MB'C'.$ $\triangle AMB' \sim \triangle MDC'$ by two angles. $\frac {AB'}{MC'} = \frac {MB'}{DC'}, MC' =\sqrt{AB' \cdot C'D} = \sqrt{6}.$

The height dropped from $M$ to $AD$ is $\sqrt{MB'^2 - (\frac{B'C'}{2})^2} =\sqrt{6 - 1} = \sqrt{5}.$

The areas of triangles $\triangle AMB'$ and $\triangle MC'B'$ are equal to $\sqrt{5},$ area of $\triangle MC'D$ is $\frac{3}{2} \sqrt{5}.$

$\triangle AMB' = \triangle AMB, \triangle MC'D = \triangle MCD \implies$ The area of $ABCD$ is $(1 + 2 + 3) \sqrt{5} = 6\sqrt{5} \implies 6^2 \cdot 5 = \boxed{180}.$

vladimir.shelomovskii@gmail.com, vvsss

Solution 4 (THINK OUTSIDE THE BOX)

Extend $AB$ and $CD$ so they intersect at a point $X$ . Then note that $M$ is the incenter of $\triangle{XAD}$ , implying that $M$ is on the angle bisector of $X$ . Now because $XM$ is both an angle bisector and a median of $\triangle{XBC}$ , $\triangle{XBC}$ is isosceles. Then we can start angle chasing:

Let $\angle{BAM}=a, \angle{CDM}=b,$ and $\angle{XBC}=c$ . Then $\angle{AMD}=\pi-(a+b), \angle{ABM}=\pi-c, \angle{DCM}=\pi-c$ , implying that $\angle{BMA}+\angle{CMD}=a+b$ , implying that $2c-(a+b)=(a+b)$ , or that $c=a+b$ . Substituting this into the rest of the diagram, we find that $\triangle{BMA} \sim \triangle{CDM} \sim \triangle{MDA}$ .

Then $\frac{AB}{BM}=\frac{MC}{CD}$ , or $BM=CM=\sqrt{6}$ . Moreover, $\frac{AB}{AM}=\frac{AM}{AD}$ , or $AM=\sqrt{14}$ . Similarly, $\frac{CD}{MD}=\frac{MD}{AD}$ , or $DM=\sqrt{21}$ . Then using Law of Cosines on $\triangle{AMD}$ , to get that $cos\angle{AMD}=-\frac{\sqrt{6}}{6}$ , or $sin\angle{AMD}=\frac{\sqrt{30}}{6}$ .

We finish by using the formula $K=\frac{1}{2}absinC$ , as follows:

$[ABCD]=[ABM]+[CDM]+[ADM]=\frac{\frac{\sqrt{30}}{6}(2\sqrt{6}+3\sqrt{6}+7\sqrt{6})}{2}=6\sqrt{5}$ .

$(6\sqrt{5})^2=\boxed{180}$ .

-dragoon

Solution 5 (incircle)

As shown in paragraph one of solution 4, extending $AB$ and $CD$ to $X$ , we realize that $\triangle{XBC}$ is isosceles, thus $XM \perp BC$ . Let $XB = XC = x$ . And, midpoint $M$ is the incenter of $\triangle{XAD}$ . Construct perpendiculars $ME, MF, MG$ to sides $AD, AX, DX$ respectively (constructing the radii of the incircle). Let $EM = FM = GM = r$ . The semiperimeter $s = \frac{2x + 2 + 3 + 7}{2} = x+6$ . Since $FX$ is the tangent off the incircle, $FX = s - AD = x-1$ . So, $BF = BX - FX = 1$ . Because $\triangle{BFM} \sim \triangle{MFX}$ ,

$\frac{BF}{FM} = \frac{FM}{FX} \implies {FM}^2 = BF \cdot FX = x - 1 \implies r^2 = x - 1$ .

By Heron's formula and the inradius area formula,

$(x+6)r = \sqrt{(x+6)\cdot 4 \cdot 3 \cdot (x-1)} \implies (x+6)r^2 = 12(x-1) \implies (x+6)(x-1) = 12(x-1) \implies x=6$

Then, $r^2 = x - 1 = 5 \implies r = \sqrt{5}$ . Finally,

$[ABCD] = [ABM] + [CDM] + [AMD] = \frac{AB \cdot FM}{2} + \frac{CD \cdot GM}{2} + \frac{AD \cdot EM}{2} = \frac{2r}{2} + \frac{3r}{2} + \frac{7r}{2} = 6r = 6\sqrt{5}$

Thus, our answer is $(6\sqrt{5})^{2} = \boxed{180}$

Remark

$B$ and $C$ are the tangent points of the X-mixtilinear incircle (of $\triangle{XAD}$ ). This may be useful, but I haven't looked into it.

~CrazyVideoGamez

Solution 6 (bash)

Let the midpoint of $BC$ be $M$ . Angle-chase and observe that $\Delta AMD~\Delta ABM~\Delta MCD$ . Let $BM=CM=a$ and $AM=x$ and $DM=y$ . As a result of this similarity, we write

$\dfrac2a=\dfrac a3,$

which gives $a=\sqrt 6$ . Similarly, we write

$\dfrac2x=\dfrac x7$

and

$\dfrac3y=\dfrac y7$

to get $x=\sqrt{14}$ and $y=\sqrt{21}$ .

We now have all required side lengths; we can find the area of $\Delta AMD$ with Heron's formula. Doing so yields $\dfrac72\sqrt5$ . We could also bash out the areas of the other two triangles since we know all their side lengths (this is what I did :sob:), but a more intelligent method is to recall the triangles' similarity. The ratio of similarlity between $\Delta AMD$ and $\Delta ABM$ is $\dfrac{\sqrt{14}}7=\sqrt{\dfrac27}$ , and between $\Delta AMD$ and $\Delta MCD$ is $\dfrac{\sqrt{21}}7=\sqrt{\dfrac37}$ . Thus, the area ratios are $\dfrac27$ and $\dfrac37$ , respectively, so adding together we have $\dfrac27+\dfrac37=\dfrac57$ . Multiplying this by our $\dfrac72\sqrt5$ , we have $\dfrac52\sqrt5$ as their total area. Adding this to our original area, we have $\dfrac52\sqrt5+\dfrac72\sqrt5=\sqrt5\left(\dfrac52+\dfrac72\right)=\sqrt5\left(\dfrac{12}2\right)=6\sqrt5$ .

The square of this is $\boxed{180}$ .

~~Technodoggo

Solution 7 (similar to 4)

As in solution 4, let $X=AB\cap CD$ , so $M$ is the incenter of $ADX$ and $XB=XC$ . Let $XB=XC=x$ . Then the normalized barycentric coordinates of $B$ , $C$ , and $M$ with respect to $ADX$ are $\left[\frac{x}{x+2}:0:\frac{2}{x+2}\right]$ , $\left[0:\frac{x}{x+3}:\frac{3}{x+3}\right]$ , and $\left[\frac{x+3}{2x+12}:\frac{x+2}{2x+12}:\frac{7}{2x+12}\right]$ . So we have $\frac{1}{2}\frac{x}{x+2}=\frac{x+3}{2x+12}$ giving $x=6$ . The sidelengths of $ADX$ are thus $AD=7$ , $AX=8$ , and $DX=9$ giving $[ADX]=12\sqrt 5$ . Also, we have $[BCX]=\frac{6}{8}\cdot\frac{6}{9}[ADX]=6\sqrt 5$ so that $[ABCD]=[ADX]-[BCX]=6\sqrt 5$ . The area squared is thus $\boxed{180}$ . ~~ golue3120

Video Solution by The Power of Logic

https://youtu.be/giLyWHKFr1I

@@ Line 1: / Line 1: @@
 ==Problem==
-Let <math>ABCD</math> be a convex quadrilateral with <math>AB=2</math>, <math>AD=7</math>, and <math>CD=3</math> such that the bisectors of acute angles <math>\angle{DAB}</math> and <math>\angle{ADC}</math> intersect at the midpoint of <math>\overline{BC}</math>. Find the square of the area of <math>ABCD</math>.
+Let <math>ABCD</math> be a convex quadrilateral with <math>AB=2, AD=7,</math> and <math>CD=3</math> such that the bisectors of acute angles <math>\angle{DAB}</math> and <math>\angle{ADC}</math> intersect at the midpoint of <math>\overline{BC}.</math> Find the square of the area of <math>ABCD.</math>
 ==Solution 1==
@@ Line 34: / Line 35: @@
 Finally, the square of the area is <math>(6\sqrt{5})^2=\boxed{180}</math>
-~DSAERF-CALMIT (https://binaryphi.site)
 ==Solution 2==
@@ Line 138: / Line 137: @@
 '''vladimir.shelomovskii@gmail.com, vvsss'''
+==Solution 4 (THINK OUTSIDE THE BOX)==
+Extend <math>AB</math> and <math>CD</math> so they intersect at a point <math>X</math>. Then note that <math>M</math> is the incenter of <math>\triangle{XAD}</math>, implying that <math>M</math> is on the angle bisector of <math>X</math>. Now because <math>XM</math> is both an angle bisector and a median of <math>\triangle{XBC}</math>, <math>\triangle{XBC}</math> is isosceles. Then we can start angle chasing:
+Let <math>\angle{BAM}=a, \angle{CDM}=b,</math> and <math>\angle{XBC}=c</math>. Then <math>\angle{AMD}=\pi-(a+b), \angle{ABM}=\pi-c, \angle{DCM}=\pi-c</math>, implying that <math>\angle{BMA}+\angle{CMD}=a+b</math>, implying that <math>2c-(a+b)=(a+b)</math>, or that <math>c=a+b</math>. Substituting this into the rest of the diagram, we find that <math>\triangle{BMA} \sim \triangle{CDM} \sim \triangle{MDA}</math>.
+Then <math>\frac{AB}{BM}=\frac{MC}{CD}</math>, or <math>BM=CM=\sqrt{6}</math>. Moreover, <math>\frac{AB}{AM}=\frac{AM}{AD}</math>, or <math>AM=\sqrt{14}</math>. Similarly, <math>\frac{CD}{MD}=\frac{MD}{AD}</math>, or <math>DM=\sqrt{21}</math>. Then using Law of Cosines on <math>\triangle{AMD}</math>, to get that <math>cos\angle{AMD}=-\frac{\sqrt{6}}{6}</math>, or <math>sin\angle{AMD}=\frac{\sqrt{30}}{6}</math>.
+We finish by using the formula <math>K=\frac{1}{2}absinC</math>, as follows:
+<math>[ABCD]=[ABM]+[CDM]+[ADM]=\frac{\frac{\sqrt{30}}{6}(2\sqrt{6}+3\sqrt{6}+7\sqrt{6})}{2}=6\sqrt{5}</math>.
+<math>(6\sqrt{5})^2=\boxed{180}</math>.
+-dragoon
+==Solution 5 (incircle)==
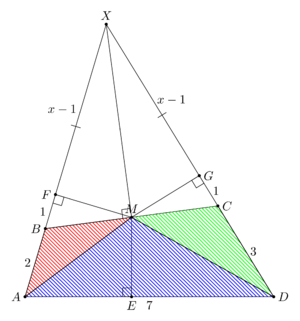
+[[File:2022_AIME_II_Problem_11_Diagram.png|300px|right]]
+As shown in paragraph one of solution 4, extending <math>AB</math> and <math>CD</math> to <math>X</math>, we realize that <math>\triangle{XBC}</math> is isosceles, thus <math>XM \perp BC</math>. Let <math>XB = XC = x</math>. And, midpoint <math>M</math> is the incenter of <math>\triangle{XAD}</math>. Construct perpendiculars <math>ME, MF, MG</math> to sides <math>AD, AX, DX</math> respectively (constructing the radii of the incircle). Let <math>EM = FM = GM = r</math>. The semiperimeter <math>s = \frac{2x + 2 + 3 + 7}{2} = x+6</math>. Since <math>FX</math> is the tangent off the incircle, <math>FX = s - AD = x-1</math>. So, <math>BF = BX - FX = 1</math>. Because <math>\triangle{BFM} \sim \triangle{MFX}</math>,
+<cmath>\frac{BF}{FM} = \frac{FM}{FX} \implies {FM}^2 = BF \cdot FX = x - 1 \implies r^2 = x - 1</cmath>.
+By Heron's formula and the inradius area formula,
+<cmath>(x+6)r = \sqrt{(x+6)\cdot 4 \cdot 3 \cdot (x-1)} \implies (x+6)r^2 = 12(x-1) \implies (x+6)(x-1) = 12(x-1) \implies x=6</cmath>
+Then,  <math>r^2 = x - 1 = 5 \implies r = \sqrt{5}</math>. Finally,
+<cmath>[ABCD] = [ABM] + [CDM] + [AMD] = \frac{AB \cdot FM}{2} + \frac{CD \cdot GM}{2} + \frac{AD \cdot EM}{2} = \frac{2r}{2} + \frac{3r}{2} + \frac{7r}{2} = 6r = 6\sqrt{5}</cmath>
+Thus, our answer is <math>(6\sqrt{5})^{2} = \boxed{180}</math>
+===Remark===
+<math>B</math> and <math>C</math> are the tangent points of the X-mixtilinear incircle (of <math>\triangle{XAD}</math>). This may be useful, but I haven't looked into it.
+~[https://artofproblemsolving.com/wiki/index.php/User:Crazyvideogamez CrazyVideoGamez]
+==Solution 6 (bash)==
+Let the midpoint of <math>BC</math> be <math>M</math>. Angle-chase and observe that <math>\Delta AMD~\Delta ABM~\Delta MCD</math>. Let <math>BM=CM=a</math> and <math>AM=x</math> and <math>DM=y</math>. As a result of this similarity, we write
+<cmath>\dfrac2a=\dfrac a3,</cmath>
+which gives <math>a=\sqrt 6</math>. Similarly, we write
+<cmath>\dfrac2x=\dfrac x7</cmath>
+and
+<cmath>\dfrac3y=\dfrac y7</cmath>
+to get <math>x=\sqrt{14}</math> and <math>y=\sqrt{21}</math>.
+We now have all required side lengths; we can find the area of <math>\Delta AMD</math> with Heron's formula. Doing so yields <math>\dfrac72\sqrt5</math>. We could also bash out the areas of the other two triangles since we know all their side lengths (this is what I did :sob:), but a more intelligent method is to recall the triangles' similarity. The ratio of similarlity between <math>\Delta AMD</math> and <math>\Delta ABM</math> is <math>\dfrac{\sqrt{14}}7=\sqrt{\dfrac27}</math>, and between <math>\Delta AMD</math> and <math>\Delta MCD</math> is <math>\dfrac{\sqrt{21}}7=\sqrt{\dfrac37}</math>. Thus, the area ratios are <math>\dfrac27</math> and <math>\dfrac37</math>, respectively, so adding together we have <math>\dfrac27+\dfrac37=\dfrac57</math>. Multiplying this by our <math>\dfrac72\sqrt5</math>, we have <math>\dfrac52\sqrt5</math> as their total area. Adding this to our original area, we have <math>\dfrac52\sqrt5+\dfrac72\sqrt5=\sqrt5\left(\dfrac52+\dfrac72\right)=\sqrt5\left(\dfrac{12}2\right)=6\sqrt5</math>.
+The square of this is <math>\boxed{180}</math>.
+~~Technodoggo
+==Solution 7 (similar to 4)==
+As in solution 4, let <math>X=AB\cap CD</math>, so <math>M</math> is the incenter of <math>ADX</math> and <math>XB=XC</math>. Let <math>XB=XC=x</math>. Then the normalized barycentric coordinates of <math>B</math>, <math>C</math>, and <math>M</math> with respect to <math>ADX</math> are <math>\left[\frac{x}{x+2}:0:\frac{2}{x+2}\right]</math>, <math>\left[0:\frac{x}{x+3}:\frac{3}{x+3}\right]</math>, and <math>\left[\frac{x+3}{2x+12}:\frac{x+2}{2x+12}:\frac{7}{2x+12}\right]</math>. So we have <math>\frac{1}{2}\frac{x}{x+2}=\frac{x+3}{2x+12}</math> giving <math>x=6</math>. The sidelengths of <math>ADX</math> are thus <math>AD=7</math>, <math>AX=8</math>, and <math>DX=9</math> giving <math>[ADX]=12\sqrt 5</math>. Also, we have <math>[BCX]=\frac{6}{8}\cdot\frac{6}{9}[ADX]=6\sqrt 5</math> so that <math>[ABCD]=[ADX]-[BCX]=6\sqrt 5</math>. The area squared is thus <math>\boxed{180}</math>.
+~~ golue3120
 ==Video Solution by The Power of Logic==

2022 AIME II (Problems • Answer Key • Resources)
Preceded by Problem 10	Followed by Problem 12
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search