Difference between revisions of "2006 Cyprus MO/Lyceum/Problems"
(→Problem 18) |
I like pie (talk | contribs) m (Problem 2 - Spacing of LaTeX) |
||
| (28 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
== Problem 1 == | == Problem 1 == | ||
| − | A diary industry, in a quantity of milk with <math>4%</math> fat adds a quantity of milk with <math>1%</math> fat and produces <math>1200</math>kg of milk with <math>2%</math> fat. | + | A diary industry, in a quantity of milk with <math>4\%</math> fat adds a quantity of milk with <math>1\%</math> fat and produces <math>1200</math>kg of milk with <math>2\%</math> fat. |
| − | The quantity of milk with <math>1%</math> fat, that was added is (in kg) | + | The quantity of milk with <math>1\%</math> fat, that was added is (in kg) |
| − | + | <math>\mathrm{(A)}\ 1000\qquad\mathrm{(B)}\ 600\qquad\mathrm{(C)}\ 800\qquad\mathrm{(D)}\ 120\qquad\mathrm{(E)}\ 480</math> | |
| − | |||
| − | B | ||
| − | |||
| − | C | ||
| − | |||
| − | D | ||
| − | |||
| − | E | ||
[[2006 Cyprus MO/Lyceum/Problem 1|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 1|Solution]] | ||
== Problem 2 == | == Problem 2 == | ||
| − | The operation <math>\alpha * \beta</math> is defined by <math>\alpha * \beta = \alpha^2 - \beta^2 | + | The operation <math>\alpha*\beta</math> is defined by <math>\alpha*\beta=\alpha^2-\beta^2\ \forall\alpha,\beta\in\mathbb{R}</math>. |
| − | The value of the expression <math>K = \left[\left(1+\sqrt{3}\right) * 2\right]*\sqrt{2} </math> is | + | The value of the expression <math>K=\left[\left(1+\sqrt{3}\right)*2\right]*\sqrt{2}</math> is |
| − | + | <math>\mathrm{(A)}\ 3\qquad\mathrm{(B)}\ 0\qquad\mathrm{(C)}\ \sqrt{3}\qquad\mathrm{(D)}\ 9\qquad\mathrm{(E)}\ 1</math> | |
| − | |||
| − | B | ||
| − | |||
| − | C | ||
| − | |||
| − | D | ||
| − | |||
| − | E | ||
[[2006 Cyprus MO/Lyceum/Problem 2|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 2|Solution]] | ||
| Line 34: | Line 18: | ||
The domain of the function <math>f(x)=\sqrt{4+2x}</math> is | The domain of the function <math>f(x)=\sqrt{4+2x}</math> is | ||
| − | + | <math>\mathrm{(A)}\ (-2,+\infty)\qquad\mathrm{(B)}\ [0,+\infty)\qquad\mathrm{(C)}\ [-2,+\infty)\qquad\mathrm{(D)}\ [-2,0]\qquad\mathrm{(E)}\ \mathbb{R}</math> | |
| − | |||
| − | B | ||
| − | |||
| − | C | ||
| − | |||
| − | D | ||
| − | |||
| − | E | ||
[[2006 Cyprus MO/Lyceum/Problem 3|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 3|Solution]] | ||
| Line 50: | Line 26: | ||
Which of the following is correct, about the graph of <math>f</math>? | Which of the following is correct, about the graph of <math>f</math>? | ||
| − | A | + | <math>\mathrm{(A)}\ \text{intersects x-axis}\qquad\mathrm{(B)}\ \text{touches y-axis}\qquad\mathrm{(C)}\ \text{touches x-axis}\qquad\mathrm{(D)}\ \text{has minimum point}\qquad\mathrm{(E)}\ \text{has maximum point}</math> |
| − | |||
| − | B | ||
| − | |||
| − | C | ||
| − | |||
| − | D | ||
| − | |||
| − | E | ||
[[2006 Cyprus MO/Lyceum/Problem 4|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 4|Solution]] | ||
| Line 65: | Line 33: | ||
If both integers <math>\alpha,\beta</math> are bigger than 1 and satisfy <math>a^7=b^8</math>, then the minimum value of <math>\alpha+\beta</math> is | If both integers <math>\alpha,\beta</math> are bigger than 1 and satisfy <math>a^7=b^8</math>, then the minimum value of <math>\alpha+\beta</math> is | ||
| − | + | <math>\mathrm{(A)}\ 384\qquad\mathrm{(B)}\ 2\qquad\mathrm{(C)}\ 15\qquad\mathrm{(D)}\ 56\qquad\mathrm{(E)}\ 512</math> | |
| − | |||
| − | B | ||
| − | |||
| − | C | ||
| − | |||
| − | D | ||
| − | |||
| − | E | ||
[[2006 Cyprus MO/Lyceum/Problem 5|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 5|Solution]] | ||
== Problem 6 == | == Problem 6 == | ||
| − | The value of the expression <math>K=\sqrt{19+ | + | The value of the expression <math>K=\sqrt{19+8\sqrt{3}}-\sqrt{7+4\sqrt{3}}</math> is |
| − | + | <math>\mathrm{(A)}\ 4\qquad\mathrm{(B)}\ 4\sqrt{3}\qquad\mathrm{(C)}\ 12+4\sqrt{3}\qquad\mathrm{(D)}\ -2\qquad\mathrm{(E)}\ 2</math> | |
| − | |||
| − | B | ||
| − | |||
| − | C | ||
| − | |||
| − | D | ||
| − | |||
| − | E | ||
[[2006 Cyprus MO/Lyceum/Problem 6|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 6|Solution]] | ||
== Problem 7 == | == Problem 7 == | ||
| − | + | [[Image:2006 CyMO-7.PNG|250px|right]] | |
| − | [[Image:2006 CyMO-7.PNG|250px]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | In the figure, <math>AB\Gamma</math> is an equilateral triangle and <math>A\Delta \perp B\Gamma</math>, <math>\Delta E\perp A\Gamma</math>, <math>EZ\perp B\Gamma</math>. If <math>EZ=\sqrt{3}</math>, then the length of the side of the triangle <math>AB\Gamma</math> is | |
| − | + | <math>\mathrm{(A)}\ \frac{3\sqrt{3}}{2}\qquad\mathrm{(B)}\ 8\qquad\mathrm{(C)}\ 4\qquad\mathrm{(D)}\ 3\qquad\mathrm{(E)}\ 9</math> | |
| − | |||
| − | E | ||
[[2006 Cyprus MO/Lyceum/Problem 7|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 7|Solution]] | ||
== Problem 8 == | == Problem 8 == | ||
| − | + | [[Image:2006 CyMO-8.PNG|250px|right]] | |
| − | [[Image:2006 CyMO-8.PNG|250px]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | In the figure <math>AB\Gamma \Delta E</math> is a regular 5-sided polygon and <math>Z</math>, <math>H</math>, <math>\Theta</math>, <math>I</math>, <math>K</math> are the points of intersections of the extensions of the sides. | |
| + | If the area of the "star" <math>AHB\Theta \Gamma I\Delta KEZA</math> is 1, then the area of the shaded quadrilateral <math>A\Gamma IZ</math> is | ||
| − | E | + | <math>\mathrm{(A)}\ \frac{2}{3}\qquad\mathrm{(B)}\ \frac{1}{2}\qquad\mathrm{(C)}\ \frac{3}{7}\qquad\mathrm{(D)}\ \frac{3}{10}\qquad\mathrm{(E)}\ \text{None of these}</math> |
[[2006 Cyprus MO/Lyceum/Problem 8|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 8|Solution]] | ||
== Problem 9 == | == Problem 9 == | ||
| − | If <math>x=\sqrt[3]{4}</math> and <math>y=\sqrt[3]{6}-\sqrt[3]{3}</math>, then which of the following is correct | + | If <math>x=\sqrt[3]{4}</math> and <math>y=\sqrt[3]{6}-\sqrt[3]{3}</math>, then which of the following is correct? |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | E | + | <math>\mathrm{(A)}\ x=y\qquad\mathrm{(B)}\ x<y\qquad\mathrm{(C)}\ x=2y\qquad\mathrm{(D)}\ x>2y\qquad\mathrm{(E)}\ \text{None of these}</math> |
[[2006 Cyprus MO/Lyceum/Problem 9|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 9|Solution]] | ||
| Line 149: | Line 73: | ||
If <math>2^x=15</math> and <math>15^y=256</math>, then the product <math>xy</math> equals | If <math>2^x=15</math> and <math>15^y=256</math>, then the product <math>xy</math> equals | ||
| − | + | <math>\mathrm{(A)}\ 7\qquad\mathrm{(B)}\ 3\qquad\mathrm{(C)}\ 1\qquad\mathrm{(D)}\ 8\qquad\mathrm{(E)}\ 6</math> | |
| − | |||
| − | B | ||
| − | |||
| − | C | ||
| − | |||
| − | D | ||
| − | |||
| − | E | ||
[[2006 Cyprus MO/Lyceum/Problem 10|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 10|Solution]] | ||
== Problem 11 == | == Problem 11 == | ||
| − | + | [[Image:2006 CyMO-11.PNG|250px|right]] | |
| − | [[Image:2006 CyMO-11.PNG|250px]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The lines <math>(\epsilon):x-2y=0</math> and <math>(\delta):x+y=4</math> intersect at the point <math>\Gamma</math>. If the line <math>(\delta)</math> intersects the axes <math>Ox</math> and <math>Oy</math> to the points <math>A</math> and <math>B</math> respectively, then the ratio of the area of the triangle <math>OA\Gamma</math> to the area of the triangle <math>OB\Gamma</math> equals | |
| − | + | <math>\mathrm{(A)}\ \frac{1}{3}\qquad\mathrm{(B)}\ \frac{2}{3}\qquad\mathrm{(C)}\ \frac{3}{5}\qquad\mathrm{(D)}\ \frac{1}{2}\qquad\mathrm{(E)}\ \frac{4}{9}</math> | |
[[2006 Cyprus MO/Lyceum/Problem 11|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 11|Solution]] | ||
== Problem 12 == | == Problem 12 == | ||
| − | If <math>f(\alpha,\beta)= \begin{cases} | + | If <math>f(\alpha,\beta)= |
then <math>f(28,17)</math> equals | then <math>f(28,17)</math> equals | ||
| − | + | <math>\mathrm{(A)}\ 8\qquad\mathrm{(B)}\ 0\qquad\mathrm{(C)}\ 11\qquad\mathrm{(D)}\ 5\qquad\mathrm{(E)}\ 1</math> | |
| − | |||
| − | B | ||
| − | |||
| − | C | ||
| − | |||
| − | D | ||
| − | |||
| − | E | ||
[[2006 Cyprus MO/Lyceum/Problem 12|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 12|Solution]] | ||
== Problem 13 == | == Problem 13 == | ||
| − | |||
The sum of the digits of the number <math>10^{2006}-2006</math> is | The sum of the digits of the number <math>10^{2006}-2006</math> is | ||
| − | + | <math>\mathrm{(A)}\ 18006\qquad\mathrm{(B)}\ 20060\qquad\mathrm{(C)}\ 2006\qquad\mathrm{(D)}\ 18047\qquad\mathrm{(E)}\ \text{None of these}</math> | |
| − | |||
| − | B | ||
| − | |||
| − | C | ||
| − | |||
| − | D | ||
| − | |||
| − | |||
[[2006 Cyprus MO/Lyceum/Problem 13|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 13|Solution]] | ||
== Problem 14 == | == Problem 14 == | ||
| − | + | [[Image:2006 CyMO-14.PNG|250px|right]] | |
| − | [[Image:2006 CyMO- | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The rectangle <math>AB\Gamma \Delta</math> is a small garden divided to the rectangle <math>AZE\Delta</math> and to the square <math>ZB\Gamma E</math>, so that <math>AE=2\sqrt{5}\ \text{m}</math> and the shaded area of the triangle <math>\Delta BE</math> is <math>4\ \text{m}^2</math>. The area of the whole garden is | |
| − | + | <math>\mathrm{(A)}\ 24\ \text{m}^2\qquad\mathrm{(B)}\ 20\ \text{m}^2\qquad\mathrm{(C)}\ 16\ \text{m}^2\qquad\mathrm{(D)}\ 32\ \text{m}^2\qquad\mathrm{(E)}\ 10\sqrt{5}\ \text{m}^2</math> | |
[[2006 Cyprus MO/Lyceum/Problem 14|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 14|Solution]] | ||
== Problem 15 == | == Problem 15 == | ||
| + | The expression <math>\frac{1}{2+\sqrt7} + \frac{1}{\sqrt7+\sqrt{10}}+ \frac{1}{\sqrt{10}+\sqrt{13}} + \frac{1}{\sqrt{13}+4}</math> equals | ||
| − | + | <math>\mathrm{(A)}\ \frac{3}{4}\qquad\mathrm{(B)}\ \frac{3}{2}\qquad\mathrm{(C)}\ \frac{2}{5}\qquad\mathrm{(D)}\ \frac{1}{2}\qquad\mathrm{(E)}\ \frac{2}{3}</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | D | ||
| − | |||
| − | E | ||
[[2006 Cyprus MO/Lyceum/Problem 15|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 15|Solution]] | ||
== Problem 16 == | == Problem 16 == | ||
| − | |||
If <math>x_1,x_2</math> are the roots of the equation <math>x^2-2kx+2m=0</math>, then <math>\frac{1}{x_1},\frac{1}{x_2}</math> are the roots of the equation | If <math>x_1,x_2</math> are the roots of the equation <math>x^2-2kx+2m=0</math>, then <math>\frac{1}{x_1},\frac{1}{x_2}</math> are the roots of the equation | ||
| − | + | <math>\mathrm{(A)}\ x^2-2k^2x+2m^2=0\qquad\mathrm{(B)}\ x^2-\frac{k}{m}x+\frac{1}{2m}=0\qquad\mathrm{(C)}\ x^2-\frac{m}{k}x+\frac{1}{2m}=0\ \mathrm{(D)}\ 2mx^2-kx+1=0\qquad\mathrm{(E)}\ 2kx^2-2mx+1=0</math> | |
| − | |||
| − | B | ||
| − | |||
| − | C | ||
| − | |||
| − | D | ||
| − | |||
| − | E | ||
[[2006 Cyprus MO/Lyceum/Problem 16|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 16|Solution]] | ||
== Problem 17 == | == Problem 17 == | ||
| − | + | [[Image:2006 CyMO-17.PNG|250px|right]] | |
| − | [[Image:2006 CyMO-17.PNG|250px]] | ||
| − | |||
| − | |||
| − | |||
| − | A. <math> | + | <math>AB\Gamma</math> is equilateral triangle of side <math>\alpha</math> and <math>A\Delta=BE=\frac{\alpha}{3}</math>. The measure of the angle <math>\ang \Gamma PE</math> is |
| − | + | <math>\mathrm{(A)}\ 60^\circ\qquad\mathrm{(B)}\ 50^\circ\qquad\mathrm{(C)}\ 40^\circ\qquad\mathrm{(D)}\ 45^\circ\qquad\mathrm{(E)}\ 70^\circ</math> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
[[2006 Cyprus MO/Lyceum/Problem 17|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 17|Solution]] | ||
== Problem 18 == | == Problem 18 == | ||
| − | + | [[Image:2006 CyMO-18.PNG|250px|right]] | |
| − | [[Image:2006 CyMO-18.PNG|250px]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <math>K(k,0)</math> is the minimum point of the parabola and the parabola intersects the y-axis at the point <math>\Gamma (0,k)</math>. | |
| + | If the area if the rectangle <math>OAB\Gamma</math> is <math>8</math>, then the equation of the parabola is | ||
| − | + | <math>\mathrm{(A)}\ y=\frac{1}{2}(x+2)^2\qquad\mathrm{(B)}\ y=\frac{1}{2}(x-2)^2\qquad\mathrm{(C)}\ y=x^2+2\qquad\mathrm{(D)}\ y=x^2-2x+1\qquad\mathrm{(E)}\ y=x^2-4x+4</math> | |
| − | |||
| − | D | ||
| − | |||
| − | E | ||
[[2006 Cyprus MO/Lyceum/Problem 18|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 18|Solution]] | ||
== Problem 19 == | == Problem 19 == | ||
| − | + | [[Image:2006 CyMO-19.PNG|250px|right]] | |
| − | [[Image:2006 CyMO-19.PNG|250px]] | ||
| − | |||
| + | In the figure, <math>AB\Gamma</math> is an isosceles triangle with<math> AB=A\Gamma=\sqrt2</math> and <math>\ang A=45^\circ</math>. If <math>B\Delta</math> is an altitude of the triangle and the sector <math>B\Lambda \Delta KB</math> belongs to the circle <math>(B,B\Delta )</math>, the area of the shaded region is | ||
| + | |||
| + | <math>\mathrm{(A)}\ \frac{4\sqrt3-\pi}{6}\qquad\mathrm{(B)}\ 4\left(\sqrt2-\frac{\pi}{3}\right)\qquad\mathrm{(C)}\ \frac{8\sqrt2-3\pi}{16}\qquad\mathrm{(D)}\ \frac{\pi}{8}\qquad\mathrm{(E)}\ \text{None of these}</math> | ||
[[2006 Cyprus MO/Lyceum/Problem 19|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 19|Solution]] | ||
== Problem 20 == | == Problem 20 == | ||
| + | The sequence <math>f:N \to R</math> satisfies <math>f(n)=f(n-1)-f(n-2),\forall n\geq 3</math>. | ||
| + | Given that <math>f(1)=f(2)=1</math>, then <math>f(3n)</math> equals | ||
| + | <math>\mathrm{(A)}\ 3\qquad\mathrm{(B)}\ -3\qquad\mathrm{(C)}\ 2\qquad\mathrm{(D)}\ 1\qquad\mathrm{(E)}\ 0</math> | ||
[[2006 Cyprus MO/Lyceum/Problem 20|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 20|Solution]] | ||
== Problem 21 == | == Problem 21 == | ||
| + | A convex polygon has <math>n</math> sides and <math>740</math> diagonals. Then <math>n</math> equals | ||
| + | |||
| + | <math>\mathrm{(A)}\ 30\qquad\mathrm{(B)}\ 40\qquad\mathrm{(C)}\ 50\qquad\mathrm{(D)}\ 60\qquad\mathrm{(E)}\ \text{None of these}</math> | ||
[[2006 Cyprus MO/Lyceum/Problem 21|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 21|Solution]] | ||
== Problem 22 == | == Problem 22 == | ||
| − | + | [[Image:2006 CyMO-22.PNG|250px|right]] | |
| − | [[Image:2006 CyMO-22.PNG|250px]] | + | |
| − | </ | + | <math>AB\Gamma \Delta</math> is rectangular and the points <math>K,\Lambda ,M,N</math> lie on the sides <math>AB, B\Gamma , \Gamma \Delta, \Delta A</math> respectively so that <math>\frac{AK}{KB}=\frac{BL}{L\Gamma}=\frac{\Gamma M}{M\Delta}=\frac{\Delta N}{NA}=2</math>. If <math>E_1</math> is the area of <math>K\Lambda MN</math> and <math>E_2</math> is the area of the rectangle <math>AB\Gamma \Delta</math>, the ratio <math>\frac{E_1}{E_2}</math> equals |
| + | <math>\mathrm{(A)}\ \frac{5}{9}\qquad\mathrm{(B)}\ \frac{1}{3}\qquad\mathrm{(C)}\ \frac{9}{5}\qquad\mathrm{(D)}\ \frac{3}{5}\qquad\mathrm{(E)}\ \text{None of these}</math> | ||
[[2006 Cyprus MO/Lyceum/Problem 22|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 22|Solution]] | ||
== Problem 23 == | == Problem 23 == | ||
| + | Of <math>21</math> students taking Mathematics, Physics and Chemistry, no student takes one subject only. The number of students taking Mathematics and Chemistry only, equals to four times the number taking Mathematics and Physics only. If the number of students taking Physics and Chemistry only equals to three times the number of students taking all three subjects, then the number of students taking all three subjects is | ||
| + | <math>\mathrm{(A)}\ 0\qquad\mathrm{(B)}\ 5\qquad\mathrm{(C)}\ 2\qquad\mathrm{(D)}\ 4\qquad\mathrm{(E)}\ 1</math> | ||
[[2006 Cyprus MO/Lyceum/Problem 23|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 23|Solution]] | ||
== Problem 24 == | == Problem 24 == | ||
| + | The number of divisors of the number <math>2006</math> is | ||
| + | <math>\mathrm{(A)}\ 3\qquad\mathrm{(B)}\ 4\qquad\mathrm{(C)}\ 8\qquad\mathrm{(D)}\ 5\qquad\mathrm{(E)}\ 6</math> | ||
[[2006 Cyprus MO/Lyceum/Problem 24|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 24|Solution]] | ||
== Problem 25 == | == Problem 25 == | ||
| − | + | {{problem}} | |
[[2006 Cyprus MO/Lyceum/Problem 25|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 25|Solution]] | ||
== Problem 26 == | == Problem 26 == | ||
| + | {{problem}} | ||
[[2006 Cyprus MO/Lyceum/Problem 26|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 26|Solution]] | ||
== Problem 27 == | == Problem 27 == | ||
| + | {{problem}} | ||
[[2006 Cyprus MO/Lyceum/Problem 27|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 27|Solution]] | ||
== Problem 28 == | == Problem 28 == | ||
| − | + | {{problem}} | |
[[2006 Cyprus MO/Lyceum/Problem 28|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 28|Solution]] | ||
== Problem 29 == | == Problem 29 == | ||
| − | + | {{problem}} | |
[[2006 Cyprus MO/Lyceum/Problem 29|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 29|Solution]] | ||
== Problem 30 == | == Problem 30 == | ||
| − | + | {{problem}} | |
[[2006 Cyprus MO/Lyceum/Problem 30|Solution]] | [[2006 Cyprus MO/Lyceum/Problem 30|Solution]] | ||
Latest revision as of 09:56, 27 April 2008
Contents
[hide]- 1 Problem 1
- 2 Problem 2
- 3 Problem 3
- 4 Problem 4
- 5 Problem 5
- 6 Problem 6
- 7 Problem 7
- 8 Problem 8
- 9 Problem 9
- 10 Problem 10
- 11 Problem 11
- 12 Problem 12
- 13 Problem 13
- 14 Problem 14
- 15 Problem 15
- 16 Problem 16
- 17 Problem 17
- 18 Problem 18
- 19 Problem 19
- 20 Problem 20
- 21 Problem 21
- 22 Problem 22
- 23 Problem 23
- 24 Problem 24
- 25 Problem 25
- 26 Problem 26
- 27 Problem 27
- 28 Problem 28
- 29 Problem 29
- 30 Problem 30
- 31 See also
Problem 1
A diary industry, in a quantity of milk with ![]() fat adds a quantity of milk with
fat adds a quantity of milk with ![]() fat and produces
fat and produces ![]() kg of milk with
kg of milk with ![]() fat.
The quantity of milk with
fat.
The quantity of milk with ![]() fat, that was added is (in kg)
fat, that was added is (in kg)
![]()
Problem 2
The operation ![]() is defined by
is defined by ![]() .
The value of the expression
.
The value of the expression ![]() is
is
![]()
Problem 3
The domain of the function ![]() is
is
![]()
Problem 4
Given the function ![]() ,
, ![]() Which of the following is correct, about the graph of
Which of the following is correct, about the graph of ![]() ?
?
![]()
Problem 5
If both integers ![]() are bigger than 1 and satisfy
are bigger than 1 and satisfy ![]() , then the minimum value of
, then the minimum value of ![]() is
is
![]()
Problem 6
The value of the expression ![]() is
is
![]()
Problem 7
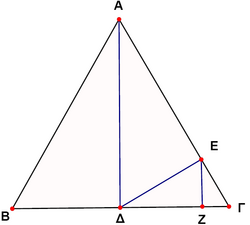
In the figure, ![]() is an equilateral triangle and
is an equilateral triangle and ![]() ,
, ![]() ,
, ![]() . If
. If ![]() , then the length of the side of the triangle
, then the length of the side of the triangle ![]() is
is
![]()
Problem 8
In the figure ![]() is a regular 5-sided polygon and
is a regular 5-sided polygon and ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() are the points of intersections of the extensions of the sides.
If the area of the "star"
are the points of intersections of the extensions of the sides.
If the area of the "star" ![]() is 1, then the area of the shaded quadrilateral
is 1, then the area of the shaded quadrilateral ![]() is
is
![]()
Problem 9
If ![]() and
and ![]() , then which of the following is correct?
, then which of the following is correct?
![]()
Problem 10
If ![]() and
and ![]() , then the product
, then the product ![]() equals
equals
![]()
Problem 11
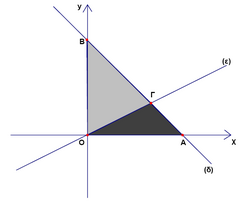
The lines ![]() and
and ![]() intersect at the point
intersect at the point ![]() . If the line
. If the line ![]() intersects the axes
intersects the axes ![]() and
and ![]() to the points
to the points ![]() and
and ![]() respectively, then the ratio of the area of the triangle
respectively, then the ratio of the area of the triangle ![]() to the area of the triangle
to the area of the triangle ![]() equals
equals
![]()
Problem 12
If 
then ![]() equals
equals
![]()
Problem 13
The sum of the digits of the number ![]() is
is
![]()
Problem 14
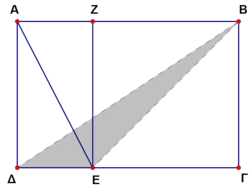
The rectangle ![]() is a small garden divided to the rectangle
is a small garden divided to the rectangle ![]() and to the square
and to the square ![]() , so that
, so that ![]() and the shaded area of the triangle
and the shaded area of the triangle ![]() is
is ![]() . The area of the whole garden is
. The area of the whole garden is
![]()
Problem 15
The expression ![]() equals
equals
![]()
Problem 16
If ![]() are the roots of the equation
are the roots of the equation ![]() , then
, then ![]() are the roots of the equation
are the roots of the equation

Problem 17
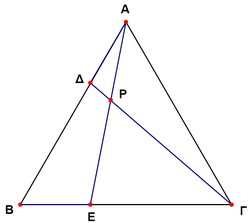
![]() is equilateral triangle of side
is equilateral triangle of side ![]() and
and ![]() . The measure of the angle $\ang \Gamma PE$ (Error compiling LaTeX. Unknown error_msg) is
. The measure of the angle $\ang \Gamma PE$ (Error compiling LaTeX. Unknown error_msg) is
![]()
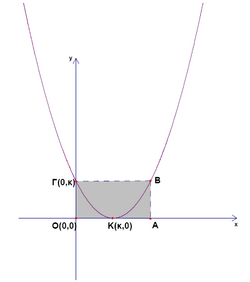
Problem 18
![]() is the minimum point of the parabola and the parabola intersects the y-axis at the point
is the minimum point of the parabola and the parabola intersects the y-axis at the point ![]() .
If the area if the rectangle
.
If the area if the rectangle ![]() is
is ![]() , then the equation of the parabola is
, then the equation of the parabola is
![]()
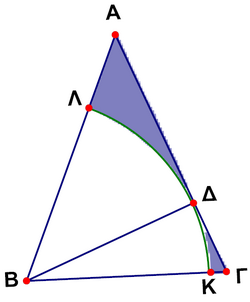
Problem 19
In the figure, ![]() is an isosceles triangle with
is an isosceles triangle with![]() and $\ang A=45^\circ$ (Error compiling LaTeX. Unknown error_msg). If
and $\ang A=45^\circ$ (Error compiling LaTeX. Unknown error_msg). If ![]() is an altitude of the triangle and the sector
is an altitude of the triangle and the sector ![]() belongs to the circle
belongs to the circle ![]() , the area of the shaded region is
, the area of the shaded region is
![]()
Problem 20
The sequence ![]() satisfies
satisfies ![]() .
Given that
.
Given that ![]() , then
, then ![]() equals
equals
![]()
Problem 21
A convex polygon has ![]() sides and
sides and ![]() diagonals. Then
diagonals. Then ![]() equals
equals
![]()
Problem 22
![]() is rectangular and the points
is rectangular and the points ![]() lie on the sides
lie on the sides ![]() respectively so that
respectively so that ![]() . If
. If ![]() is the area of
is the area of ![]() and
and ![]() is the area of the rectangle
is the area of the rectangle ![]() , the ratio
, the ratio ![]() equals
equals
![]()
Problem 23
Of ![]() students taking Mathematics, Physics and Chemistry, no student takes one subject only. The number of students taking Mathematics and Chemistry only, equals to four times the number taking Mathematics and Physics only. If the number of students taking Physics and Chemistry only equals to three times the number of students taking all three subjects, then the number of students taking all three subjects is
students taking Mathematics, Physics and Chemistry, no student takes one subject only. The number of students taking Mathematics and Chemistry only, equals to four times the number taking Mathematics and Physics only. If the number of students taking Physics and Chemistry only equals to three times the number of students taking all three subjects, then the number of students taking all three subjects is
![]()
Problem 24
The number of divisors of the number ![]() is
is
![]()
Problem 25
This problem has not been edited in. If you know this problem, please help us out by adding it.
Problem 26
This problem has not been edited in. If you know this problem, please help us out by adding it.
Problem 27
This problem has not been edited in. If you know this problem, please help us out by adding it.
Problem 28
This problem has not been edited in. If you know this problem, please help us out by adding it.
Problem 29
This problem has not been edited in. If you know this problem, please help us out by adding it.
Problem 30
This problem has not been edited in. If you know this problem, please help us out by adding it.