Difference between revisions of "1997 AIME Problems/Problem 6"
(solution) |
Talkinaway (talk | contribs) (→Solution) |
||
| Line 2: | Line 2: | ||
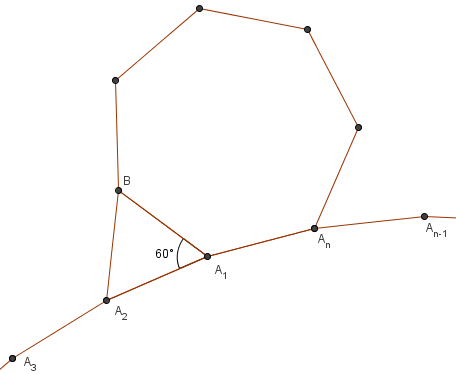
[[Point]] <math>B</math> is in the exterior of the [[regular polygon|regular]] <math>n</math>-sided polygon <math>A_1A_2\cdots A_n</math>, and <math>A_1A_2B</math> is an [[equilateral triangle]]. What is the largest value of <math>n</math> for which <math>A_1</math>, <math>A_n</math>, and <math>B</math> are consecutive vertices of a regular polygon? | [[Point]] <math>B</math> is in the exterior of the [[regular polygon|regular]] <math>n</math>-sided polygon <math>A_1A_2\cdots A_n</math>, and <math>A_1A_2B</math> is an [[equilateral triangle]]. What is the largest value of <math>n</math> for which <math>A_1</math>, <math>A_n</math>, and <math>B</math> are consecutive vertices of a regular polygon? | ||
| − | == Solution == | + | == Solution 1== |
[[Image:1997_AIME-6.png]] | [[Image:1997_AIME-6.png]] | ||
| Line 19: | Line 19: | ||
\end{eqnarray*}</cmath> | \end{eqnarray*}</cmath> | ||
Clearly <math>n</math> is maximized when <math>m = 7, n = \boxed{42}</math>. | Clearly <math>n</math> is maximized when <math>m = 7, n = \boxed{42}</math>. | ||
| + | |||
| + | == Solution 2 == | ||
| + | |||
| + | As above, find that <math>mn - 6m - 6n = 0</math> using the formula for the interior angle of a polygon. | ||
| + | |||
| + | Solve for <math>n</math> to find that <math>n = \frac{6m}{m-6}</math>. Clearly, <math>m>6</math> for <math>n</math> to be positive. | ||
| + | |||
| + | With this restriction of <math>m>6</math>, the larger <math>m</math> gets, the smaller the fraction <math>\frac{6m}{m-6}</math> becomes. This can be proven either by calculus, by noting that <math>n = \frac{6m}{m-6}</math> is a transformed hyperbola, or by dividing out the rational function to get <math>n = 6 + \frac{36}{m - 6}.</math> | ||
| + | |||
| + | Either way, minimizng <math>m</math> will maximize <math>n</math>, and the smallest integer <math>m</math> such that <math>n</math> is positive is <math>m=7</math>, giving <math>n = \boxed{42}</math> | ||
== See also == | == See also == | ||
Revision as of 16:48, 10 June 2011
Contents
[hide]Problem
Point ![]() is in the exterior of the regular
is in the exterior of the regular ![]() -sided polygon
-sided polygon ![]() , and
, and ![]() is an equilateral triangle. What is the largest value of
is an equilateral triangle. What is the largest value of ![]() for which
for which ![]() ,
, ![]() , and
, and ![]() are consecutive vertices of a regular polygon?
are consecutive vertices of a regular polygon?
Solution 1
Let the other regular polygon have ![]() sides. Using the interior angle of a regular polygon formula, we have
sides. Using the interior angle of a regular polygon formula, we have ![]() ,
, ![]() , and
, and ![]() . Since those three angles add up to
. Since those three angles add up to ![]() ,
,
 Using SFFT,
Using SFFT,
![]() Clearly
Clearly ![]() is maximized when
is maximized when ![]() .
.
Solution 2
As above, find that ![]() using the formula for the interior angle of a polygon.
using the formula for the interior angle of a polygon.
Solve for ![]() to find that
to find that ![]() . Clearly,
. Clearly, ![]() for
for ![]() to be positive.
to be positive.
With this restriction of ![]() , the larger
, the larger ![]() gets, the smaller the fraction
gets, the smaller the fraction ![]() becomes. This can be proven either by calculus, by noting that
becomes. This can be proven either by calculus, by noting that ![]() is a transformed hyperbola, or by dividing out the rational function to get
is a transformed hyperbola, or by dividing out the rational function to get ![]()
Either way, minimizng ![]() will maximize
will maximize ![]() , and the smallest integer
, and the smallest integer ![]() such that
such that ![]() is positive is
is positive is ![]() , giving
, giving ![]()
See also
| 1997 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 5 |
Followed by Problem 7 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||