Difference between revisions of "1997 AIME Problems/Problem 6"
m |
m (→Solution 3) |
||
| (6 intermediate revisions by 5 users not shown) | |||
| Line 1: | Line 1: | ||
== Problem == | == Problem == | ||
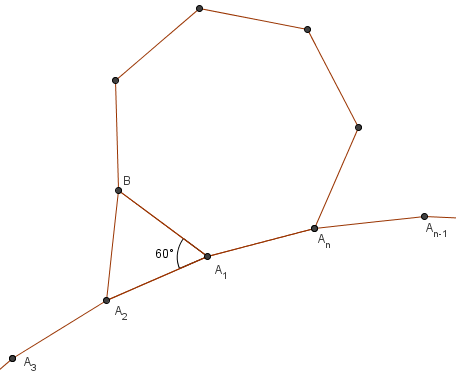
| − | Point <math>B</math> is in the exterior of the regular <math>n</math>-sided polygon <math>A_1A_2\cdots A_n</math>, and <math>A_1A_2B</math> is an equilateral triangle. What is the largest value of <math>n</math> for which <math>A_1</math>, <math>A_n</math>, and <math>B</math> are consecutive vertices of a regular polygon? | + | [[Point]] <math>B</math> is in the exterior of the [[regular polygon|regular]] <math>n</math>-sided polygon <math>A_1A_2\cdots A_n</math>, and <math>A_1A_2B</math> is an [[equilateral triangle]]. What is the largest value of <math>n</math> for which <math>A_1</math>, <math>A_n</math>, and <math>B</math> are consecutive vertices of a regular polygon? |
| − | == Solution == | + | == Solution 1== |
| − | {{ | + | [[Image:1997_AIME-6.png]] |
| + | |||
| + | Let the other regular polygon have <math>m</math> sides. Using the interior angle of a regular polygon formula, we have <math>\angle A_2A_1A_n = \frac{(n-2)180}{n}</math>, <math>\angle A_nA_1B = \frac{(m-2)180}{m}</math>, and <math>\angle A_2A_1B = 60^{\circ}</math>. Since those three angles add up to <math>360^{\circ}</math>, | ||
| + | |||
| + | <cmath>\begin{eqnarray*} | ||
| + | \frac{(n-2)180}{n} + \frac{(m-2)180}{m} &=& 300\ | ||
| + | m(n-2)180 + n(m-2)180 &=& 300mn\ | ||
| + | 360mn - 360m - 360n &=& 300mn\ | ||
| + | mn - 6m - 6n &=& 0 | ||
| + | \end{eqnarray*}</cmath> | ||
| + | Using [[Simon's Favorite Factoring Trick|SFFT]], | ||
| + | |||
| + | <cmath>\begin{eqnarray*} | ||
| + | (m-6)(n-6) &=& 36 | ||
| + | \end{eqnarray*}</cmath> | ||
| + | Clearly <math>n</math> is maximized when <math>m = 7, n = \boxed{042}</math>. | ||
| + | |||
| + | == Solution 2 == | ||
| + | |||
| + | As above, find that <math>mn - 6m - 6n = 0</math> using the formula for the interior angle of a polygon. | ||
| + | |||
| + | Solve for <math>n</math> to find that <math>n = \frac{6m}{m-6}</math>. Clearly, <math>m>6</math> for <math>n</math> to be positive. | ||
| + | |||
| + | With this restriction of <math>m>6</math>, the larger <math>m</math> gets, the smaller the fraction <math>\frac{6m}{m-6}</math> becomes. This can be proven either by calculus, by noting that <math>n = \frac{6m}{m-6}</math> is a transformed hyperbola, or by dividing out the rational function to get <math>n = 6 + \frac{36}{m - 6}.</math> | ||
| + | |||
| + | Either way, minimizng <math>m</math> will maximize <math>n</math>, and the smallest integer <math>m</math> such that <math>n</math> is positive is <math>m=7</math>, giving <math>n = \boxed{042}</math> | ||
| + | |||
| + | == Solution 3 == | ||
| + | |||
| + | From the formula for the measure for an individual angle of a regular n-gon, <math>180 - \frac{360}{n}</math>, the measure of <math>\angle A_2A_1A_n = 180 - \frac{360}{n}</math>. Together with the fact that an equilateral triangle has angles measuring 60 degrees, the measure of <math>\angle A_nA_1B = 120 + \frac{360}{n}</math> (Notice that this value decreases as <math>n</math> increases; hence, we are looking for the least possible value of <math>\angle A_nA_1B</math>). For <math>A_n, A_1, B</math> to be vertices of a regular polygon, <math>\angle A_nA_1B</math> must be of the form <math>180 - \frac{360}{n}</math>, where <math>n</math> is a natural number greater than or equal to 3. It is obvious that <math>\angle A_nA_1B > 120</math>. The least angle satisfying this condition is <math>180 - \frac{360}{7}</math>. Equating this with <math>120 + \frac{360}{n}</math> and solving yields <math>n = \boxed{042}</math> | ||
== See also == | == See also == | ||
{{AIME box|year=1997|num-b=5|num-a=7}} | {{AIME box|year=1997|num-b=5|num-a=7}} | ||
| + | |||
| + | [[Category:Intermediate Algebra Problems]] | ||
| + | [[Category:Intermediate Geometry Problems]] | ||
| + | {{MAA Notice}} | ||
Latest revision as of 23:39, 21 December 2018
Contents
[hide]Problem
Point ![]() is in the exterior of the regular
is in the exterior of the regular ![]() -sided polygon
-sided polygon ![]() , and
, and ![]() is an equilateral triangle. What is the largest value of
is an equilateral triangle. What is the largest value of ![]() for which
for which ![]() ,
, ![]() , and
, and ![]() are consecutive vertices of a regular polygon?
are consecutive vertices of a regular polygon?
Solution 1
Let the other regular polygon have ![]() sides. Using the interior angle of a regular polygon formula, we have
sides. Using the interior angle of a regular polygon formula, we have ![]() ,
, ![]() , and
, and ![]() . Since those three angles add up to
. Since those three angles add up to ![]() ,
,
 Using SFFT,
Using SFFT,
![]() Clearly
Clearly ![]() is maximized when
is maximized when ![]() .
.
Solution 2
As above, find that ![]() using the formula for the interior angle of a polygon.
using the formula for the interior angle of a polygon.
Solve for ![]() to find that
to find that ![]() . Clearly,
. Clearly, ![]() for
for ![]() to be positive.
to be positive.
With this restriction of ![]() , the larger
, the larger ![]() gets, the smaller the fraction
gets, the smaller the fraction ![]() becomes. This can be proven either by calculus, by noting that
becomes. This can be proven either by calculus, by noting that ![]() is a transformed hyperbola, or by dividing out the rational function to get
is a transformed hyperbola, or by dividing out the rational function to get ![]()
Either way, minimizng ![]() will maximize
will maximize ![]() , and the smallest integer
, and the smallest integer ![]() such that
such that ![]() is positive is
is positive is ![]() , giving
, giving ![]()
Solution 3
From the formula for the measure for an individual angle of a regular n-gon, ![]() , the measure of
, the measure of ![]() . Together with the fact that an equilateral triangle has angles measuring 60 degrees, the measure of
. Together with the fact that an equilateral triangle has angles measuring 60 degrees, the measure of ![]() (Notice that this value decreases as
(Notice that this value decreases as ![]() increases; hence, we are looking for the least possible value of
increases; hence, we are looking for the least possible value of ![]() ). For
). For ![]() to be vertices of a regular polygon,
to be vertices of a regular polygon, ![]() must be of the form
must be of the form ![]() , where
, where ![]() is a natural number greater than or equal to 3. It is obvious that
is a natural number greater than or equal to 3. It is obvious that ![]() . The least angle satisfying this condition is
. The least angle satisfying this condition is ![]() . Equating this with
. Equating this with ![]() and solving yields
and solving yields ![]()
See also
| 1997 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 5 |
Followed by Problem 7 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()