Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1983 AHSME Problems/Problem 23"

m (Improved readability)
m (Improved clarity/formatting and added box at the bottom)
 
Line 37: Line 37:
 
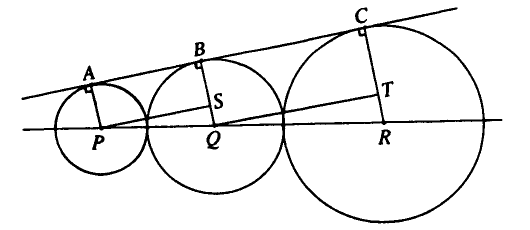
Consider three consecutive circles, as shown in the diagram above; observe that their centres <math>P</math>, <math>Q</math>, and <math>R</math> are collinear by symmetry. Let <math>A</math>, <math>B</math>, and <math>C</math> be the points of tangency, and let <math>PS</math> and <math>QT</math> be segments parallel to the upper tangent (i.e. <math>L_1</math>), as also shown. Since <math>PQ</math> is parallel to <math>QR</math> (the three points are collinear), <math>PS</math> is parallel to <math>QT</math> (as both are parallel to <math>L_1</math>), and <math>SQ</math> is parallel to <math>TR</math> (as both are perpendicular to <math>L_1</math>, due to the tangent being perpendicular to the radius), we have <math>\triangle PQS \sim \triangle QRT</math>.
 
Consider three consecutive circles, as shown in the diagram above; observe that their centres <math>P</math>, <math>Q</math>, and <math>R</math> are collinear by symmetry. Let <math>A</math>, <math>B</math>, and <math>C</math> be the points of tangency, and let <math>PS</math> and <math>QT</math> be segments parallel to the upper tangent (i.e. <math>L_1</math>), as also shown. Since <math>PQ</math> is parallel to <math>QR</math> (the three points are collinear), <math>PS</math> is parallel to <math>QT</math> (as both are parallel to <math>L_1</math>), and <math>SQ</math> is parallel to <math>TR</math> (as both are perpendicular to <math>L_1</math>, due to the tangent being perpendicular to the radius), we have <math>\triangle PQS \sim \triangle QRT</math>.
  
−
Now, if we let <math>x, y</math>, and <math>z</math> be the radii of the three circles (from smallest to largest), then <math>QS = y - x</math> and <math>RT = z - y</math>. Thus, from the similarity that we just proved, <math>\frac{QS}{PQ} = \frac{RT}{QR} \Rightarrow \frac{y-x}{x+y} = \frac{z-y}{y+z}</math> (where e.g. <math>PQ = x + y</math> because of collinearity). This actually simplifies to <math>y^2 = zx</math>, i.e. <math>\frac{y}{x} = \frac{z}{y}</math>, so the ratio of consecutive radii is constant, forming a geometric sequence. In this case, as the first radius is <math>8</math> and, four radii later, the radius is <math>18</math>, this constant ratio is <math>\sqrt[\leftroot{-2}\uproot{2}{4}]{\frac{18}{8}}</math>. Therefore the middle radius is <math>8 \cdot {\left(\sqrt[\leftroot{-2}\uproot{2}{4}]{\frac{18}{8}}\right)}^{2} = 8 \sqrt{\frac{18}{8}} = \sqrt{18 \cdot 8} = \sqrt{144} = 12</math>, which is choice <math>\boxed{\textbf{A}}</math>.
+
Now, if we let <math>x, y</math>, and <math>z</math> be the radii of the three circles (from smallest to largest), then <math>QS = y - x</math> and <math>RT = z - y</math>. Thus, from the similarity that we just proved, <math>\frac{QS}{PQ} = \frac{RT}{QR} \Rightarrow \frac{y-x}{x+y} = \frac{z-y}{y+z}</math> (where e.g. <math>PQ = x + y</math> because of collinearity). This equation reduces to <math>y^2 = zx</math>, i.e. <math>\frac{y}{x} = \frac{z}{y}</math>, so the ratio of consecutive radii is constant, forming a geometric sequence. In this case, as the first radius is <math>8</math> and, four radii later, the radius is <math>18</math>, this constant ratio is <math>\sqrt[\leftroot{-2}\uproot{2}{4}]{\frac{18}{8}}</math>. Therefore the middle radius is <math>8 \cdot {\left(\sqrt[\leftroot{-2}\uproot{2}{4}]{\frac{18}{8}}\right)}^{2} = 8 \sqrt{\frac{18}{8}} = \sqrt{18 \cdot 8} = \sqrt{144} = 12</math>, which is choice <math>\boxed{\textbf{(A)}}</math>.
 +
 
 +
==See Also==
 +
{{AHSME box|year=1983|num-b=22|num-a=24}}
 +
 
 +
{{MAA Notice}}

Latest revision as of 00:01, 20 February 2019

Problem

In the adjoining figure the five circles are tangent to one another consecutively and to the lines $L_1$ and $L_2$. If the radius of the largest circle is $18$ and that of the smallest one is $8$, then the radius of the middle circle is

[asy] size(250);defaultpen(linewidth(0.7)); real alpha=5.797939254, x=71.191836; int i; for(i=0; i<5; i=i+1) { real r=8*(sqrt(6)/2)^i; draw(Circle((x+r)*dir(alpha), r)); x=x+2r; } real x=71.191836+40+20*sqrt(6), r=18; pair A=tangent(origin, (x+r)*dir(alpha), r, 1), B=tangent(origin, (x+r)*dir(alpha), r, 2); pair A1=300*dir(origin--A), B1=300*dir(origin--B); draw(B1--origin--A1); pair X=(69,-5), X1=reflect(origin, (x+r)*dir(alpha))*X, Y=(200,-5), Y1=reflect(origin, (x+r)*dir(alpha))*Y, Z=(130,0), Z1=reflect(origin, (x+r)*dir(alpha))*Z; clip(X--Y--Y1--X1--cycle); label("$L_2$", Z, S); label("$L_1$", Z1, dir(2*alpha)*dir(90));[/asy]

$\textbf{(A)} \ 12 \qquad \textbf{(B)} \ 12.5 \qquad \textbf{(C)} \ 13 \qquad \textbf{(D)} \ 13.5 \qquad \textbf{(E)} \ 14$

Solution

Pdfresizer.com-pdf-convert-q23.png

Consider three consecutive circles, as shown in the diagram above; observe that their centres $P$, $Q$, and $R$ are collinear by symmetry. Let $A$, $B$, and $C$ be the points of tangency, and let $PS$ and $QT$ be segments parallel to the upper tangent (i.e. $L_1$), as also shown. Since $PQ$ is parallel to $QR$ (the three points are collinear), $PS$ is parallel to $QT$ (as both are parallel to $L_1$), and $SQ$ is parallel to $TR$ (as both are perpendicular to $L_1$, due to the tangent being perpendicular to the radius), we have $\triangle PQS \sim \triangle QRT$.

Now, if we let $x, y$, and $z$ be the radii of the three circles (from smallest to largest), then $QS = y - x$ and $RT = z - y$. Thus, from the similarity that we just proved, $\frac{QS}{PQ} = \frac{RT}{QR} \Rightarrow \frac{y-x}{x+y} = \frac{z-y}{y+z}$ (where e.g. $PQ = x + y$ because of collinearity). This equation reduces to $y^2 = zx$, i.e. $\frac{y}{x} = \frac{z}{y}$, so the ratio of consecutive radii is constant, forming a geometric sequence. In this case, as the first radius is $8$ and, four radii later, the radius is $18$, this constant ratio is $\sqrt[\leftroot{-2}\uproot{2}{4}]{\frac{18}{8}}$. Therefore the middle radius is $8 \cdot {\left(\sqrt[\leftroot{-2}\uproot{2}{4}]{\frac{18}{8}}\right)}^{2} = 8 \sqrt{\frac{18}{8}} = \sqrt{18 \cdot 8} = \sqrt{144} = 12$, which is choice $\boxed{\textbf{(A)}}$.

See Also

1983 AHSME (Problems • Answer Key • Resources)
Preceded by
Problem 22 		Followed by
Problem 24
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30
All AHSME Problems and Solutions


The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1983_AHSME_Problems/Problem_23&oldid=103581"