Difference between revisions of "2022 AIME II Problems/Problem 15"
(Created page with "/") |
Bobjoebilly (talk | contribs) m (→Solution 3) |
||
| (29 intermediate revisions by 11 users not shown) | |||
| Line 1: | Line 1: | ||
| − | / | + | ==Problem== |
| + | |||
| + | Two externally tangent circles <math>\omega_1</math> and <math>\omega_2</math> have centers <math>O_1</math> and <math>O_2</math>, respectively. A third circle <math>\Omega</math> passing through <math>O_1</math> and <math>O_2</math> intersects <math>\omega_1</math> at <math>B</math> and <math>C</math> and <math>\omega_2</math> at <math>A</math> and <math>D</math>, as shown. Suppose that <math>AB = 2</math>, <math>O_1O_2 = 15</math>, <math>CD = 16</math>, and <math>ABO_1CDO_2</math> is a convex hexagon. Find the area of this hexagon. | ||
| + | <asy> | ||
| + | import geometry; | ||
| + | size(10cm); | ||
| + | point O1=(0,0),O2=(15,0),B=9*dir(30); | ||
| + | circle w1=circle(O1,9),w2=circle(O2,6),o=circle(O1,O2,B); | ||
| + | point A=intersectionpoints(o,w2)[1],D=intersectionpoints(o,w2)[0],C=intersectionpoints(o,w1)[0]; | ||
| + | filldraw(A--B--O1--C--D--O2--cycle,0.2*fuchsia+white,black); | ||
| + | draw(w1); | ||
| + | draw(w2); | ||
| + | draw(O1--O2,dashed); | ||
| + | draw(o); | ||
| + | dot(O1); | ||
| + | dot(O2); | ||
| + | dot(A); | ||
| + | dot(D); | ||
| + | dot(C); | ||
| + | dot(B); | ||
| + | label("$\omega_1$",8*dir(110),SW); | ||
| + | label("$\omega_2$",5*dir(70)+(15,0),SE); | ||
| + | label("$O_1$",O1,W); | ||
| + | label("$O_2$",O2,E); | ||
| + | label("$B$",B,N+1/2*E); | ||
| + | label("$A$",A,N+1/2*W); | ||
| + | label("$C$",C,S+1/4*W); | ||
| + | label("$D$",D,S+1/4*E); | ||
| + | label("$15$",midpoint(O1--O2),N); | ||
| + | label("$16$",midpoint(C--D),N); | ||
| + | label("$2$",midpoint(A--B),S); | ||
| + | label("$\Omega$",o.C+(o.r-1)*dir(270)); | ||
| + | </asy> | ||
| + | |||
| + | ==Solution 1== | ||
| + | First observe that <math>AO_2 = O_2D</math> and <math>BO_1 = O_1C</math>. Let points <math>A'</math> and <math>B'</math> be the reflections of <math>A</math> and <math>B</math>, respectively, about the perpendicular bisector of <math>\overline{O_1O_2}</math>. Then quadrilaterals <math>ABO_1O_2</math> and <math>B'A'O_2O_1</math> are congruent, so hexagons <math>ABO_1CDO_2</math> and <math>A'B'O_1CDO_2</math> have the same area. Furthermore, triangles <math>DO_2A'</math> and <math>B'O_1C</math> are congruent, so <math>A'D = B'C</math> and quadrilateral <math>A'B'CD</math> is an isosceles trapezoid. | ||
| + | <asy> | ||
| + | import olympiad; | ||
| + | size(180); | ||
| + | defaultpen(linewidth(0.7)); | ||
| + | pair Ap = dir(105), Bp = dir(75), O1 = dir(25), C = dir(320), D = dir(220), O2 = dir(175); | ||
| + | draw(unitcircle^^Ap--Bp--O1--C--D--O2--cycle); | ||
| + | label("$A'$",Ap,dir(origin--Ap)); | ||
| + | label("$B'$",Bp,dir(origin--Bp)); | ||
| + | label("$O_1$",O1,dir(origin--O1)); | ||
| + | label("$C$",C,dir(origin--C)); | ||
| + | label("$D$",D,dir(origin--D)); | ||
| + | label("$O_2$",O2,dir(origin--O2)); | ||
| + | draw(O2--O1,linetype("4 4")); | ||
| + | draw(Ap--D^^Bp--C,linetype("2 2")); | ||
| + | </asy> | ||
| + | Next, remark that <math>B'O_1 = DO_2</math>, so quadrilateral <math>B'O_1DO_2</math> is also an isosceles trapezoid; in turn, <math>B'D = O_1O_2 = 15</math>, and similarly <math>A'C = 15</math>. Thus, Ptolmey's theorem on <math>A'B'CD</math> yields <math>A'D\cdot B'C + 2\cdot 16 = 15^2</math>, whence <math>A'D = B'C = \sqrt{193}</math>. Let <math>\alpha = \angle A'B'D</math>. The Law of Cosines on triangle <math>A'B'D</math> yields | ||
| + | <cmath>\cos\alpha = \frac{15^2 + 2^2 - (\sqrt{193})^2}{2\cdot 2\cdot 15} = \frac{36}{60} = \frac 35,</cmath> and hence <math>\sin\alpha = \tfrac 45</math>. Thus the distance between bases <math>A’B’</math> and <math>CD</math> is <math>12</math> (in fact, <math>\triangle A'B'D</math> is a <math>9-12-15</math> triangle with a <math>7-12-\sqrt{193}</math> triangle removed), which implies the area of <math>A'B'CD</math> is <math>\tfrac12\cdot 12\cdot(2+16) = 108</math>. | ||
| + | |||
| + | Now let <math>O_1C = O_2A' = r_1</math> and <math>O_2D = O_1B' = r_2</math>; the tangency of circles <math>\omega_1</math> and <math>\omega_2</math> implies <math>r_1 + r_2 = 15</math>. Furthermore, angles <math>A'O_2D</math> and <math>A'B'D</math> are opposite angles in cyclic quadrilateral <math>B'A'O_2D</math>, which implies the measure of angle <math>A'O_2D</math> is <math>180^\circ - \alpha</math>. Therefore, the Law of Cosines applied to triangle <math>\triangle A'O_2D</math> yields | ||
| + | <cmath>\begin{align*} | ||
| + | 193 &= r_1^2 + r_2^2 - 2r_1r_2(-\tfrac 35) = (r_1^2 + 2r_1r_2 + r_2^2) - \tfrac45r_1r_2\\ | ||
| + | &= (r_1+r_2)^2 - \tfrac45 r_1r_2 = 225 - \tfrac45r_1r_2. | ||
| + | \end{align*}</cmath> | ||
| + | |||
| + | Thus <math>r_1r_2 = 40</math>, and so the area of triangle <math>A'O_2D</math> is <math>\tfrac12r_1r_2\sin\alpha = 16</math>. | ||
| + | |||
| + | Thus, the area of hexagon <math>ABO_{1}CDO_{2}</math> is <math>108 + 2\cdot 16 = \boxed{140}</math>. | ||
| + | |||
| + | ~djmathman | ||
| + | |||
| + | ==Solution 2== | ||
| + | |||
| + | Denote by <math>O</math> the center of <math>\Omega</math>. | ||
| + | Denote by <math>r</math> the radius of <math>\Omega</math>. | ||
| + | |||
| + | We have <math>O_1</math>, <math>O_2</math>, <math>A</math>, <math>B</math>, <math>C</math>, <math>D</math> are all on circle <math>\Omega</math>. | ||
| + | |||
| + | Denote <math>\angle O_1 O O_2 = 2 \theta</math>. | ||
| + | Denote <math>\angle O_1 O B = \alpha</math>. | ||
| + | Denote <math>\angle O_2 O A = \beta</math>. | ||
| + | |||
| + | Because <math>B</math> and <math>C</math> are on circles <math>\omega_1</math> and <math>\Omega</math>, <math>BC</math> is a perpendicular bisector of <math>O_1 O</math>. Hence, <math>\angle O_1 O C = \alpha</math>. | ||
| + | |||
| + | Because <math>A</math> and <math>D</math> are on circles <math>\omega_2</math> and <math>\Omega</math>, <math>AD</math> is a perpendicular bisector of <math>O_2 O</math>. Hence, <math>\angle O_2 O D = \beta</math>. | ||
| + | |||
| + | In <math>\triangle O O_1 O_2</math>, | ||
| + | <cmath> | ||
| + | \[ | ||
| + | O_1 O_2 = 2 r \sin \theta . | ||
| + | \] | ||
| + | </cmath> | ||
| + | |||
| + | Hence, | ||
| + | <cmath> | ||
| + | \[ | ||
| + | 2 r \sin \theta = 15 . | ||
| + | \] | ||
| + | </cmath> | ||
| + | |||
| + | In <math>\triangle O AB</math>, | ||
| + | <cmath> | ||
| + | \begin{align*} | ||
| + | AB & = 2 r \sin \frac{2 \theta - \alpha - \beta}{2} \\ | ||
| + | & = 2 r \sin \theta \cos \frac{\alpha + \beta}{2} | ||
| + | - 2 r \cos \theta \sin \frac{\alpha + \beta}{2} \\ | ||
| + | & = 15 \cos \frac{\alpha + \beta}{2} | ||
| + | - 2 r \cos \theta \sin \frac{\alpha + \beta}{2} . | ||
| + | \end{align*} | ||
| + | </cmath> | ||
| + | |||
| + | Hence, | ||
| + | <cmath> | ||
| + | \[ | ||
| + | 15 \cos \frac{\alpha + \beta}{2} | ||
| + | - 2 r \cos \theta \sin \frac{\alpha + \beta}{2} | ||
| + | = 2 . \hspace{1cm} (1) | ||
| + | \] | ||
| + | </cmath> | ||
| + | |||
| + | |||
| + | In <math>\triangle O CD</math>, | ||
| + | <cmath> | ||
| + | \begin{align*} | ||
| + | CD & = 2 r \sin \frac{360^\circ - 2 \theta - \alpha - \beta}{2} \\ | ||
| + | & = 2 r \sin \left( \theta + \frac{\alpha + \beta}{2} \right) \\ | ||
| + | & = 2 r \sin \theta \cos \frac{\alpha + \beta}{2} | ||
| + | + 2 r \cos \theta \sin \frac{\alpha + \beta}{2} \\ | ||
| + | & = 15 \cos \frac{\alpha + \beta}{2} | ||
| + | + 2 r \cos \theta \sin \frac{\alpha + \beta}{2} . | ||
| + | \end{align*} | ||
| + | </cmath> | ||
| + | |||
| + | Hence, | ||
| + | <cmath> | ||
| + | \[ | ||
| + | 15 \cos \frac{\alpha + \beta}{2} | ||
| + | + 2 r \cos \theta \sin \frac{\alpha + \beta}{2} | ||
| + | = 16 . \hspace{1cm} (2) | ||
| + | \] | ||
| + | </cmath> | ||
| + | |||
| + | Taking <math>\frac{(1) + (2)}{30}</math>, we get <math>\cos \frac{\alpha + \beta}{2} = \frac{3}{5}</math>. | ||
| + | Thus, <math>\sin \frac{\alpha + \beta}{2} = \frac{4}{5}</math>. | ||
| + | |||
| + | Taking these into (1), we get <math>2 r \cos \theta = \frac{35}{4}</math>. | ||
| + | Hence, | ||
| + | <cmath> | ||
| + | \begin{align*} | ||
| + | 2 r & = \sqrt{ \left( 2 r \sin \theta \right)^2 + \left( 2 r \cos \theta \right)^2} \\ | ||
| + | & = \frac{5}{4} \sqrt{193} . | ||
| + | \end{align*} | ||
| + | </cmath> | ||
| + | |||
| + | Hence, <math>\cos \theta = \frac{7}{\sqrt{193}}</math>. | ||
| + | |||
| + | In <math>\triangle O O_1 B</math>, | ||
| + | <cmath> | ||
| + | \[ | ||
| + | O_1 B = 2 r \sin \frac{\alpha}{2} . | ||
| + | \] | ||
| + | </cmath> | ||
| + | |||
| + | In <math>\triangle O O_2 A</math>, by applying the law of sines, we get | ||
| + | <cmath> | ||
| + | \[ | ||
| + | O_2 A = 2 r \sin \frac{\beta}{2} . | ||
| + | \] | ||
| + | </cmath> | ||
| + | |||
| + | Because circles <math>\omega_1</math> and <math>\omega_2</math> are externally tangent, <math>B</math> is on circle <math>\omega_1</math>, <math>A</math> is on circle <math>\omega_2</math>, | ||
| + | <cmath> | ||
| + | \begin{align*} | ||
| + | O_1 O_2 & = O_1 B + O_2 A \\ | ||
| + | & = 2 r \sin \frac{\alpha}{2} + 2 r \sin \frac{\beta}{2} \\ | ||
| + | & = 2 r \left( \sin \frac{\alpha}{2} + \sin \frac{\beta}{2} \right) . | ||
| + | \end{align*} | ||
| + | </cmath> | ||
| + | |||
| + | Thus, <math>\sin \frac{\alpha}{2} + \sin \frac{\beta}{2} = \frac{12}{\sqrt{193}}</math>. | ||
| + | |||
| + | Now, we compute <math>\sin \alpha</math> and <math>\sin \beta</math>. | ||
| + | |||
| + | Recall <math>\cos \frac{\alpha + \beta}{2} = \frac{3}{5}</math> and <math>\sin \frac{\alpha + \beta}{2} = \frac{4}{5}</math>. | ||
| + | Thus, <math>e^{i \frac{\alpha}{2}} e^{i \frac{\beta}{2}} = e^{i \frac{\alpha + \beta}{2}} = \frac{3}{5} + i \frac{4}{5}</math>. | ||
| + | |||
| + | We also have | ||
| + | <cmath> | ||
| + | \begin{align*} | ||
| + | \sin \frac{\alpha}{2} + \sin \frac{\beta}{2} | ||
| + | & = \frac{1}{2i} \left( e^{i \frac{\alpha}{2}} - e^{-i \frac{\alpha}{2}} | ||
| + | + e^{i \frac{\beta}{2}} - e^{-i \frac{\beta}{2}} \right) \\ | ||
| + | & = \frac{1}{2i} \left( 1 - \frac{1}{e^{i \frac{\alpha + \beta}{2}} } \right) | ||
| + | \left( e^{i \frac{\alpha}{2}} + e^{i \frac{\beta}{2}} \right) | ||
| + | . | ||
| + | \end{align*} | ||
| + | </cmath> | ||
| + | |||
| + | Thus, | ||
| + | <cmath> | ||
| + | \begin{align*} | ||
| + | \sin \alpha + \sin \beta | ||
| + | & = \frac{1}{2i} \left( e^{i \alpha} - e^{-i \alpha} | ||
| + | + e^{i \beta} - e^{-i \beta} \right) \\ | ||
| + | & = \frac{1}{2i} \left( 1 - \frac{1}{e^{i \left( \alpha + \beta \right)}} \right) | ||
| + | \left( e^{i \alpha} + e^{i \beta} \right) \\ | ||
| + | & = \frac{1}{2i} \left( 1 - \frac{1}{e^{i \left( \alpha + \beta \right)}} \right) | ||
| + | \left( | ||
| + | \left( e^{i \frac{\alpha}{2}} + e^{i \frac{\beta}{2}} \right)^2 | ||
| + | - 2 e^{i \frac{\alpha + \beta}{2}} | ||
| + | \right) \\ | ||
| + | & = \frac{1}{2i} \left( 1 - \frac{1}{e^{i \left( \alpha + \beta \right)}} \right) | ||
| + | \left( | ||
| + | \left( \frac{2 i \left( \sin \frac{\alpha}{2} + \sin \frac{\beta}{2} \right)}{1 - \frac{1}{e^{i \frac{\alpha + \beta}{2}} }} \right)^2 | ||
| + | - 2 e^{i \frac{\alpha + \beta}{2}} | ||
| + | \right) \\ | ||
| + | & = - \frac{1}{i} \left( e^{i \frac{\alpha + \beta}{2}} - e^{-i \frac{\alpha + \beta}{2}} \right) | ||
| + | \left( | ||
| + | \frac{2 \left( \sin \frac{\alpha}{2} + \sin \frac{\beta}{2} \right)^2} | ||
| + | {e^{i \frac{\alpha + \beta}{2}} + e^{-i \frac{\alpha + \beta}{2}} - 2 } | ||
| + | + 1 | ||
| + | \right) \\ | ||
| + | & = \frac{167 \cdot 8}{193 \cdot 5 } . | ||
| + | \end{align*} | ||
| + | </cmath> | ||
| + | |||
| + | Therefore, | ||
| + | <cmath> | ||
| + | \begin{align*} | ||
| + | {\rm Area} \ ABO_1CDO_2 | ||
| + | & = {\rm Area} \ \triangle O_3 AB + {\rm Area} \ \triangle O_3 BO_1 | ||
| + | + {\rm Area} \ \triangle O_3 O_1 C \\ | ||
| + | & \quad + {\rm Area} \ \triangle O_3 C D | ||
| + | + {\rm Area} \ \triangle O_3 D O_2 + {\rm Area} \ \triangle O_3 O_2 A \\ | ||
| + | & = \frac{1}{2} r^2 \left( | ||
| + | \sin \left( 2 \theta - \alpha - \beta \right) + \sin \alpha + \sin \alpha | ||
| + | + \sin \left( 360^\circ - 2 \theta - \alpha - \beta \right) | ||
| + | + \sin \beta + \sin \beta \right) \\ | ||
| + | & = \frac{1}{2} r^2 \left( | ||
| + | \sin \left( 2 \theta - \alpha - \beta \right) | ||
| + | - \sin \left( 2 \theta + \alpha + \beta \right) | ||
| + | + 2 \sin \alpha + 2 \sin \beta | ||
| + | \right) \\ | ||
| + | & = r^2 \left( | ||
| + | - \cos 2 \theta \sin \left( \alpha + \beta \right) | ||
| + | + \sin \alpha + \sin \beta | ||
| + | \right) \\ | ||
| + | & = r^2 \left( \left( 1 - 2 \cos^2 \theta \right) 2 \sin \frac{\alpha + \beta}{2} \cos \frac{\alpha + \beta}{2} | ||
| + | + \sin \alpha + \sin \beta \right) \\ | ||
| + | & = \boxed{\textbf{(140) }} . | ||
| + | \end{align*} | ||
| + | </cmath> | ||
| + | |||
| + | ~Steven Chen (www.professorchenedu.com) | ||
| + | |||
| + | ==Solution 3== | ||
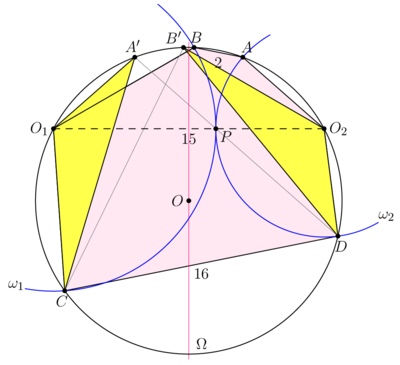
| + | [[File:AIME-II-2022-15.png|400px|right]] | ||
| + | Let points <math>A'</math> and <math>B'</math> be the reflections of <math>A</math> and <math>B,</math> respectively, about the perpendicular bisector of <math>O_1 O_2.</math> | ||
| + | <cmath>B'O_2 = BO_1 = O_1 P = O_1 C,</cmath> | ||
| + | <cmath>A'O_1 = AO_2 = O_2 P = O_2 D.</cmath> | ||
| + | We establish the equality of the arcs and conclude that the corresponding chords are equal | ||
| + | <cmath>\overset{\Large\frown} {CO_1} + \overset{\Large\frown} {A'O_1} +\overset{\Large\frown} {A'B'} = \overset{\Large\frown} {B'O_2} +\overset{\Large\frown} {A'O_1} +\overset{\Large\frown} {A'B'} =\overset{\Large\frown} {B'O_2} +\overset{\Large\frown} {DO_2} +\overset{\Large\frown} {A'B'}</cmath> | ||
| + | <cmath> \implies A'D = B'C = O_1 O_2 = 15.</cmath> | ||
| + | Similarly <math>A'C = B'D \implies \triangle A'CO_1 = \triangle B'DO_2.</math> | ||
| + | |||
| + | Ptolemy's theorem on <math>A'CDB'</math> yields <cmath>B'D \cdot A'C + A'B' \cdot CD = A'D \cdot B'C \implies</cmath> | ||
| + | <cmath> B'D^2 + 2 \cdot 16 = 15^2 \implies B'D = A'C = \sqrt{193}.</cmath> | ||
| + | The area of the trapezoid <math>A'CDB'</math> is equal to the area of an isosceles triangle with sides | ||
| + | <math>A'D = B'C = 15</math> and <math>A'B' + CD = 18.</math> | ||
| + | |||
| + | The height of this triangle is <math>\sqrt{15^2-9^2} = 12.</math> The area of <math>A'CDB'</math> is <math>108.</math> | ||
| + | |||
| + | <cmath>\sin \angle B'CD = \frac{12}{15} = \frac{4}{5},</cmath> | ||
| + | <cmath>\angle B'CD + \angle B'O_2 D = 180^o \implies \sin \angle B'O_2 D = \frac{4}{5}.</cmath> | ||
| + | |||
| + | Denote <math>\angle B'O_2 D = 2\alpha.</math> | ||
| + | <math>\angle B'O_2 D > \frac{\pi}{2},</math> hence <math>\cos \angle B'O_2 D = \cos 2\alpha = -\frac{3}{5}.</math> | ||
| + | <cmath>\tan \alpha =\frac { \sin 2 \alpha}{1+\cos 2 \alpha} = \frac {4/5}{1 - 3/5}=2.</cmath> | ||
| + | |||
| + | Semiperimeter of <math>\triangle B'O_2 D </math> is <math>s = \frac {15 + \sqrt{193}}{2}.</math> | ||
| + | |||
| + | The distance from the vertex <math>O_2</math> to the tangent points of the inscribed circle of the triangle <math>B'O_2 D</math> is equal <math>s – B'D = \frac{15 – \sqrt{193}}{2}.</math> | ||
| + | |||
| + | The radius of the inscribed circle is <math>r = (s – B'D) \tan \alpha.</math> | ||
| + | |||
| + | The area of triangle <math>B'O_2 D</math> is <math>[B'O_2 D] = sr = s (s – B'D) \tan \alpha = \frac {15^2 – 193}{2} = 16.</math> | ||
| + | |||
| + | The hexagon <math>ABO_1 CDO_2</math> has the same area as hexagon <math>B'A'O_1 CDO_2.</math> | ||
| + | |||
| + | The area of hexagon <math>B'A'O_1 CDO_2</math> is equal to the sum of the area of the trapezoid <math>A'CDB'</math> and the areas of two equal triangles <math>B'O_2 D</math> and <math>A'O_1 C,</math> so the area of the hexagon <math>ABO_1 CDO_2</math> is <cmath>108 + 16 + 16 = \boxed{140}.</cmath> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
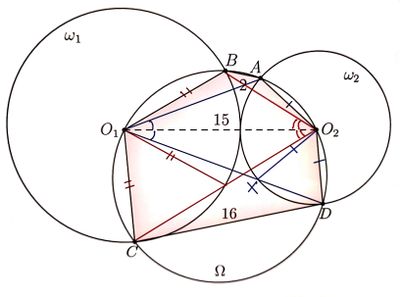
| + | ==Solution 4== | ||
| + | |||
| + | |||
| + | [[File:AIME 2022 II Prob15.jpg|400px|top]] | ||
| + | |||
| + | |||
| + | Let circle <math>O_1</math>'s radius be <math>r</math>, then the radius of circle <math>O_2</math> is <math>15-r</math>. Based on Brahmagupta's Formula, | ||
| + | |||
| + | |||
| + | the hexagon's Area <math>= \sqrt{14(1)(16-r)(1+r)} + \sqrt{7(8)(23-r)(8+r)}</math>. | ||
| + | |||
| + | |||
| + | Now we only need to find the <math>r</math>. | ||
| + | |||
| + | |||
| + | Connect <math>O_1</math> and <math>A</math> , <math>O_1</math> and <math>D</math> , and let <math>X</math> be the point of intersection between <math>O_1D</math> and circle <math>O_2</math> , based on the " 2 Non-Congruent Triangles of 'SSA' Scenario " , we can immediately see <math>O_1X = O_1A</math> and therefore get an equation from the "Power of A Point Theorem: | ||
| + | |||
| + | |||
| + | <math>(O_1A)(O_1D) = r(15+15-r) = 15r + r(15-r)</math> (1). | ||
| + | |||
| + | |||
| + | Similarly, | ||
| + | |||
| + | |||
| + | <math>(O_2B)(O_2C) = (15-r)(15+r) = 15(15-r) + r(15-r)</math> (2). | ||
| + | |||
| + | |||
| + | We can also get two other equations about these 4 segments from Ptolemy's Theorem: | ||
| + | |||
| + | |||
| + | <math>(O_1A)(O_2B) = 30 + r(15-r)</math> (3) | ||
| + | |||
| + | |||
| + | <math>(O_1D)(O_2C) = 240 + r(15-r)</math> (4) | ||
| + | |||
| + | |||
| + | Multiply equations (1) and (2), and equations (3) and (4) respectively, we will get a very simple and nice equation of <math>r</math>: | ||
| + | |||
| + | |||
| + | <math>2(15^2)r(15-r) = 7200 + 270r(15-r)</math>, | ||
| + | |||
| + | |||
| + | then: | ||
| + | |||
| + | |||
| + | <math>r(15-r) = 40</math>. | ||
| + | |||
| + | |||
| + | This result is good enough for us to find the hexagon's area, which: | ||
| + | |||
| + | <math>= \sqrt{14(1)(16-r)(1+r)} + \sqrt{7(8)(23-r)(8+r)}</math> | ||
| + | <math>= \sqrt{14(1)(1+15-r)(1+r)} + \sqrt{7(8)(8+15-r)(8+r)}</math> | ||
| + | <math>= \sqrt{14(1)(1+15+40)} + \sqrt{7(8)(64+8(15)+40)}</math> | ||
| + | <math>= 28 + 112 = \boxed{\textbf{140}}</math>. | ||
| + | |||
| + | eJMaSc | ||
| + | |||
| + | |||
| + | ==Video Solution== | ||
| + | https://youtu.be/TeAWS5H5bcc | ||
| + | |||
| + | ~MathProblemSolvingSkills.com | ||
| + | |||
| + | |||
| + | ==See Also== | ||
| + | {{AIME box|year=2022|n=II|num-b=14|after=Last Problem}} | ||
| + | |||
| + | [[Category:Intermediate Geometry Problems]] | ||
| + | {{MAA Notice}} | ||
Latest revision as of 23:28, 28 June 2023
Problem
Two externally tangent circles ![]() and
and ![]() have centers
have centers ![]() and
and ![]() , respectively. A third circle
, respectively. A third circle ![]() passing through
passing through ![]() and
and ![]() intersects
intersects ![]() at
at ![]() and
and ![]() and
and ![]() at
at ![]() and
and ![]() , as shown. Suppose that
, as shown. Suppose that ![]() ,
, ![]() ,
, ![]() , and
, and ![]() is a convex hexagon. Find the area of this hexagon.
is a convex hexagon. Find the area of this hexagon.
![[asy] import geometry; size(10cm); point O1=(0,0),O2=(15,0),B=9*dir(30); circle w1=circle(O1,9),w2=circle(O2,6),o=circle(O1,O2,B); point A=intersectionpoints(o,w2)[1],D=intersectionpoints(o,w2)[0],C=intersectionpoints(o,w1)[0]; filldraw(A--B--O1--C--D--O2--cycle,0.2*fuchsia+white,black); draw(w1); draw(w2); draw(O1--O2,dashed); draw(o); dot(O1); dot(O2); dot(A); dot(D); dot(C); dot(B); label("$\omega_1$",8*dir(110),SW); label("$\omega_2$",5*dir(70)+(15,0),SE); label("$O_1$",O1,W); label("$O_2$",O2,E); label("$B$",B,N+1/2*E); label("$A$",A,N+1/2*W); label("$C$",C,S+1/4*W); label("$D$",D,S+1/4*E); label("$15$",midpoint(O1--O2),N); label("$16$",midpoint(C--D),N); label("$2$",midpoint(A--B),S); label("$\Omega$",o.C+(o.r-1)*dir(270)); [/asy]](http://latex.artofproblemsolving.com/7/b/9/7b94456c42eaed4f905c8c8fbc0555d154676d57.png)
Solution 1
First observe that ![]() and
and ![]() . Let points
. Let points ![]() and
and ![]() be the reflections of
be the reflections of ![]() and
and ![]() , respectively, about the perpendicular bisector of
, respectively, about the perpendicular bisector of ![]() . Then quadrilaterals
. Then quadrilaterals ![]() and
and ![]() are congruent, so hexagons
are congruent, so hexagons ![]() and
and ![]() have the same area. Furthermore, triangles
have the same area. Furthermore, triangles ![]() and
and ![]() are congruent, so
are congruent, so ![]() and quadrilateral
and quadrilateral ![]() is an isosceles trapezoid.
is an isosceles trapezoid.
![[asy] import olympiad; size(180); defaultpen(linewidth(0.7)); pair Ap = dir(105), Bp = dir(75), O1 = dir(25), C = dir(320), D = dir(220), O2 = dir(175); draw(unitcircle^^Ap--Bp--O1--C--D--O2--cycle); label("$A'$",Ap,dir(origin--Ap)); label("$B'$",Bp,dir(origin--Bp)); label("$O_1$",O1,dir(origin--O1)); label("$C$",C,dir(origin--C)); label("$D$",D,dir(origin--D)); label("$O_2$",O2,dir(origin--O2)); draw(O2--O1,linetype("4 4")); draw(Ap--D^^Bp--C,linetype("2 2")); [/asy]](http://latex.artofproblemsolving.com/8/a/4/8a4698486f5397ef610a64ee840efec7ff7e7c21.png) Next, remark that
Next, remark that ![]() , so quadrilateral
, so quadrilateral ![]() is also an isosceles trapezoid; in turn,
is also an isosceles trapezoid; in turn, ![]() , and similarly
, and similarly ![]() . Thus, Ptolmey's theorem on
. Thus, Ptolmey's theorem on ![]() yields
yields ![]() , whence
, whence ![]() . Let
. Let ![]() . The Law of Cosines on triangle
. The Law of Cosines on triangle ![]() yields
yields
![]() and hence
and hence ![]() . Thus the distance between bases
. Thus the distance between bases ![]() and
and ![]() is
is ![]() (in fact,
(in fact, ![]() is a
is a ![]() triangle with a
triangle with a ![]() triangle removed), which implies the area of
triangle removed), which implies the area of ![]() is
is ![]() .
.
Now let ![]() and
and ![]() ; the tangency of circles
; the tangency of circles ![]() and
and ![]() implies
implies ![]() . Furthermore, angles
. Furthermore, angles ![]() and
and ![]() are opposite angles in cyclic quadrilateral
are opposite angles in cyclic quadrilateral ![]() , which implies the measure of angle
, which implies the measure of angle ![]() is
is ![]() . Therefore, the Law of Cosines applied to triangle
. Therefore, the Law of Cosines applied to triangle ![]() yields
yields

Thus ![]() , and so the area of triangle
, and so the area of triangle ![]() is
is ![]() .
.
Thus, the area of hexagon ![]() is
is ![]() .
.
~djmathman
Solution 2
Denote by ![]() the center of
the center of ![]() .
Denote by
.
Denote by ![]() the radius of
the radius of ![]() .
.
We have ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() are all on circle
are all on circle ![]() .
.
Denote ![]() .
Denote
.
Denote ![]() .
Denote
.
Denote ![]() .
.
Because ![]() and
and ![]() are on circles
are on circles ![]() and
and ![]() ,
, ![]() is a perpendicular bisector of
is a perpendicular bisector of ![]() . Hence,
. Hence, ![]() .
.
Because ![]() and
and ![]() are on circles
are on circles ![]() and
and ![]() ,
, ![]() is a perpendicular bisector of
is a perpendicular bisector of ![]() . Hence,
. Hence, ![]() .
.
In ![]() ,
,
![]()
Hence,
![]()
In ![]() ,
,

Hence,
![]()
In ![]() ,
,

Hence,
![]()
Taking ![]() , we get
, we get ![]() .
Thus,
.
Thus, ![]() .
.
Taking these into (1), we get ![]() .
Hence,
.
Hence,

Hence, ![]() .
.
In ![]() ,
,
![]()
In ![]() , by applying the law of sines, we get
, by applying the law of sines, we get
![]()
Because circles ![]() and
and ![]() are externally tangent,
are externally tangent, ![]() is on circle
is on circle ![]() ,
, ![]() is on circle
is on circle ![]() ,
,

Thus, ![]() .
.
Now, we compute ![]() and
and ![]() .
.
Recall ![]() and
and ![]() .
Thus,
.
Thus, ![]() .
.
We also have

Thus,

Therefore,

~Steven Chen (www.professorchenedu.com)
Solution 3
Let points ![]() and
and ![]() be the reflections of
be the reflections of ![]() and
and ![]() respectively, about the perpendicular bisector of
respectively, about the perpendicular bisector of ![]()
![]()
![]() We establish the equality of the arcs and conclude that the corresponding chords are equal
We establish the equality of the arcs and conclude that the corresponding chords are equal
![]()
![]() Similarly
Similarly ![]()
Ptolemy's theorem on ![]() yields
yields ![]()
![]() The area of the trapezoid
The area of the trapezoid ![]() is equal to the area of an isosceles triangle with sides
is equal to the area of an isosceles triangle with sides
![]() and
and ![]()
The height of this triangle is ![]() The area of
The area of ![]() is
is ![]()
![]()
![]()
Denote ![]()
![]() hence
hence ![]()
![]()
Semiperimeter of ![]() is
is ![]()
The distance from the vertex ![]() to the tangent points of the inscribed circle of the triangle
to the tangent points of the inscribed circle of the triangle ![]() is equal
is equal ![]()
The radius of the inscribed circle is ![]()
The area of triangle ![]() is
is ![]()
The hexagon ![]() has the same area as hexagon
has the same area as hexagon ![]()
The area of hexagon ![]() is equal to the sum of the area of the trapezoid
is equal to the sum of the area of the trapezoid ![]() and the areas of two equal triangles
and the areas of two equal triangles ![]() and
and ![]() so the area of the hexagon
so the area of the hexagon ![]() is
is ![]()
vladimir.shelomovskii@gmail.com, vvsss
Solution 4
Let circle ![]() 's radius be
's radius be ![]() , then the radius of circle
, then the radius of circle ![]() is
is ![]() . Based on Brahmagupta's Formula,
. Based on Brahmagupta's Formula,
the hexagon's Area ![]() .
.
Now we only need to find the ![]() .
.
Connect ![]() and
and ![]() ,
, ![]() and
and ![]() , and let
, and let ![]() be the point of intersection between
be the point of intersection between ![]() and circle
and circle ![]() , based on the " 2 Non-Congruent Triangles of 'SSA' Scenario " , we can immediately see
, based on the " 2 Non-Congruent Triangles of 'SSA' Scenario " , we can immediately see ![]() and therefore get an equation from the "Power of A Point Theorem:
and therefore get an equation from the "Power of A Point Theorem:
![]() (1).
(1).
Similarly,
![]() (2).
(2).
We can also get two other equations about these 4 segments from Ptolemy's Theorem:
![]() (3)
(3)
![]() (4)
(4)
Multiply equations (1) and (2), and equations (3) and (4) respectively, we will get a very simple and nice equation of ![]() :
:
![]() ,
,
then:
![]() .
.
This result is good enough for us to find the hexagon's area, which:



.
eJMaSc
Video Solution
~MathProblemSolvingSkills.com
See Also
| 2022 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Problem | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.