Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 Fall AMC 12B Problems/Problem 17"

(→‎Solution 3)
(→‎Solution 5 (Casework))
 
(25 intermediate revisions by 5 users not shown)
Line 6: Line 6:
 
\frac{4}{27} \qquad\textbf{(E)}\ \frac{1}{16}</math>
 
\frac{4}{27} \qquad\textbf{(E)}\ \frac{1}{16}</math>
  
−
==Solution 1==
+
==Solution 1 (Recursion)==
 
Let <math>S(n)</math> be the number of paths of <math>n</math> moves such that the bug never will have been more than <math>1</math> unit away from the starting position. Clearly, by symmetry, there are two possible states here, the bug being on the center and the bug being on one of the vertices of the unit hexagon around the center. Let <math>C(n)</math> be the number of paths with the aforementioned restriction that end on the center. Let <math>V(n)</math> be the number of paths with the aforementioned restriction that end on a vertex of the surrounding unit hexagon. We have <math>S(n) = 6C(n-1) + 3V(n-1),</math> since from the center, there are <math>6</math> possible points to land to and from a vertex there are <math>3</math> possible points to land to (the two adjacent vertices and the center). We also have <math>C(n) = V(n-1)</math>, since to get to the center the bug must have come from a vertex, and <math>V(n) = 2V(n-1) + 6C(n-1),</math> since from a vertex there are two vertices to move to, and from the center there are <math>6</math> vertices to move to. We can construct a recursion table using the base cases <math>V(1) = 6</math> and <math>C(1) = 0</math> and our recursive rules for <math>C(n)</math> and <math>V(n)</math> as follows:  
 
Let <math>S(n)</math> be the number of paths of <math>n</math> moves such that the bug never will have been more than <math>1</math> unit away from the starting position. Clearly, by symmetry, there are two possible states here, the bug being on the center and the bug being on one of the vertices of the unit hexagon around the center. Let <math>C(n)</math> be the number of paths with the aforementioned restriction that end on the center. Let <math>V(n)</math> be the number of paths with the aforementioned restriction that end on a vertex of the surrounding unit hexagon. We have <math>S(n) = 6C(n-1) + 3V(n-1),</math> since from the center, there are <math>6</math> possible points to land to and from a vertex there are <math>3</math> possible points to land to (the two adjacent vertices and the center). We also have <math>C(n) = V(n-1)</math>, since to get to the center the bug must have come from a vertex, and <math>V(n) = 2V(n-1) + 6C(n-1),</math> since from a vertex there are two vertices to move to, and from the center there are <math>6</math> vertices to move to. We can construct a recursion table using the base cases <math>V(1) = 6</math> and <math>C(1) = 0</math> and our recursive rules for <math>C(n)</math> and <math>V(n)</math> as follows:  
−
<cmath>\begin{tabular}{c|c|c} n & V(n) & C(n) \\ \hline
+
<cmath>\begin{array}{c|c|c}
 +
n & V(n) & C(n) \\ \hline
 +
& & \\ [-2ex]
 
1 & 6 & 0 \\
 
1 & 6 & 0 \\
 
2 & 12 & 6 \\
 
2 & 12 & 6 \\
 
3 & 60 & 12 \\
 
3 & 60 & 12 \\
 
4 & 192 & 60 \\
 
4 & 192 & 60 \\
−
\end{tabular}</cmath>
+
\end{array}</cmath>
−
Then, <math>S(5) = 6C(4) + 3V(4) = 6 \cdot 60 + 3 \cdot 192 = 936,</math> and the desired probability is thus <math>\frac{936}{6^5} = \boxed{\frac{13}{108}}.</math>
+
Then, <math>S(5) = 6C(4) + 3V(4) = 6 \cdot 60 + 3 \cdot 192 = 936,</math> and the desired probability is thus <math>\frac{936}{6^5} = \boxed{\textbf{(A)}\ \frac{13}{108}}.</math>
  
−
-fidgetboss_4000
+
~fidgetboss_4000
  
−
== Solution 2 ==
+
==Solution 2 (Recursion)==
−
We use <math>\left( n , t \right)</math> to denote the bug's current state.
+
 
 +
Let <math>p(i)</math> be such probability after <math>i</math> moves. <math>p(1)=1</math>, <math>p(2)=\frac{1}{2}</math>. Then, <math>p(3)=\frac{1}{3}\cdot \frac{1}{2}+\frac{1}{6}\cdot 1=\frac{1}{3}</math>. Then, we can prove the recursive formula <cmath>p(x)=\frac{1}{3}p(x-1)+\frac{1}{6}p(x-2).</cmath> Now, we evaluate <math>p(5)=\boxed{\textbf{(A)}\ \frac{13}{108}}</math>.
 +
 
 +
== Solution 3 (Recursion) ==
 +
We use <math>(n,t)</math> to denote the bug's current state. We wish to find <math>P(0,5)</math>.
  
 
The first argument <math>n</math> denotes the bug's current position.
 
The first argument <math>n</math> denotes the bug's current position.
 
We use <math>n = 0</math> to denote the bug's starting point.
 
We use <math>n = 0</math> to denote the bug's starting point.
−
We use <math>n = 1</math> to denote any point whose distance to the bug's starting point is 1.
+
We use <math>n = 1</math> to denote any point whose distance to the bug's starting point is <math>1</math>.
  
 
The second argument <math>t</math> denotes the remaining number of moves the bug has.
 
The second argument <math>t</math> denotes the remaining number of moves the bug has.
  
−
For <math>n = 0</math> and <math>t \geq 1</math>,
+
For <math>n = 0</math> and <math>t \geq 1</math>, we have <cmath>P(0,t) = P(1,t-1).</cmath>
−
<cmath>
+
For <math>n = 1</math> and <math>t \geq 1</math>, we have <cmath>P(1,t) = \frac{1}{6} P(0,t-1) + \frac{1}{3} P(1,t-1).</cmath>
−
\begin{align*}
+
For <math>n \in \left\{ 0 , 1 \right\}</math> and <math>t = 0</math>, we have <cmath>P(n,0) = 1.</cmath>
−
P \left( 0 , t \right) & = P \left( 1 , t - 1 \right) .
+
We solve this recursive equation by using backward induction:
−
\end{align*}
+
<cmath>\begin{array}{ll}
−
</cmath>
+
P(0,1) = 1, & P(1,1) = \frac{1}{2}, \\ [1ex]
 +
P(0,2) = \frac{1}{2}, & P(1,2) = \frac{1}{3}, \\ [1ex]
 +
P(0,3) = \frac{1}{3}, & P(1,3) = \frac{7}{36}, \\ [1ex]
 +
P(0,4) = \frac{7}{36}, & P(1,4) = \frac{13}{108}.
 +
\end{array}</cmath>
 +
Therefore, the answer is <math>P(0,5) = P(1,4) = \boxed{\textbf{(A)}\ \frac{13}{108}}</math>.
 +
 
 +
~Steven Chen (www.professorchenedu.com)
 +
 
 +
==Solution 4 (Generating Function)==
 +
 
 +
Use a generating function, define <math>c_{n}\cdot x^{n}</math> be <math>c_{n}</math> ways for the destination be <math>n</math> units away from the origin.
 +
 
 +
We conclude that:
 +
 
 +
* If the current point is origin, then we need to multiply by <math>6x</math>.
 +
 
 +
* If the current point on vertex of the unit hexagon, then we need to multiply by <math>x^{-1}+2</math>, where there is <math>1</math> way to return to the origin and there are two ways to keep distance <math>1</math>.
 +
 
 +
Now let's start with <math>p(x)=1</math>.
 +
 
 +
<math>1</math>st step:  <math>p(x)=6x</math> 
 +
 
 +
<math>2</math>nd step:  <math>p(x)=6x\cdot(x^{-1}+2) = 6 + 12x </math>
 +
 
 +
<math>3</math>rd step:  <math>p(x)=6\cdot6x + 12x\cdot(x^{-1}+2) = 12 + 60x</math>
 +
 
 +
<math>4</math>th step:  <math>p(x)=12\cdot6x + 60x\cdot(x^{-1}+2) = 60 + 192x </math>
 +
 
 +
<math>5</math>th step:  <math>p(x)=60\cdot6x + 192x\cdot(x^{-1}+2) = 192 + 744x </math>
  
−
For <math>n = 1</math> and <math>t \geq 1</math>,
+
So, there are <math>192+744=936</math> ways for the bug never moves more than <math>1</math> unit away from origin. The answer is <math>\frac{936}{6^5} = \boxed{\textbf{(A)}\ \frac{13}{108}}</math>.
−
<cmath>
 
−
\begin{align*}
 
−
P \left( 1 , t \right) & = \frac{1}{6} P \left( 0 ,  t - 1 \right)
 
−
+ \frac{1}{3} P \left( 1 , t - 1 \right)  .
 
−
\end{align*}
 
−
</cmath>
 
  
−
For <math>n \in \left\{ 0 , 1 \right\}</math> and <math>t = 0</math>,
+
~wwei.yu
−
<cmath>
 
−
\begin{align*}
 
−
P \left( n , 0 \right) & = 1 .
 
−
\end{align*}
 
−
</cmath>
 
  
−
We solve this recursive equation by using backward induction.
+
==Solution 5 (Casework)==
  
−
We get
+
In the following diagram, let <math>A</math> denote the vertex where the bug starts (shown in red) and <math>B</math> denote one of the <math>6</math> adjacent vertices (shown in green).
−
<cmath>
+
<asy>
−
\[
+
/* Made by MRENTHUSIASM */
−
P \left( 0 , 1 \right) = 1 , \hspace{1cm}
+
size(150);
−
P \left( 1 , 1 \right) = \frac{1}{2}
+
pair[] A, B, C;
−
\]
+
for (int i = 0; i <= 5; ++i) {
−
</cmath>
+
A[i] = dir(60*i);
−
and
+
    B[i] = 2 * dir(60*i);
−
<cmath>
+
    C[i] = sqrt(3) * dir(30+60i);
−
\[
+
}
−
P \left( 0 , 2 \right) = \frac{1}{2} , \hspace{1cm}
+
draw(B[2]--B[3]^^C[1]--C[3]^^B[1]--B[4]^^C[0]--C[4]^^B[0]--B[5]^^B[3]--B[4]^^C[2]--C[4]^^B[2]--B[5]^^C[1]--C[5]^^B[1]--B[0]^^B[2]--B[1]^^C[2]--C[0]^^B[3]--B[0]^^C[3]--C[5]^^B[4]--B[5]);
−
P \left( 1 , 2 \right) = \frac{1}{3}
+
dot(origin,red+linewidth(5));
−
\]
+
for (int i = 0; i <= 5; ++i) {
−
</cmath>
+
    dot(A[i],green+linewidth(5));
−
and
+
    dot(B[i],linewidth(5));
−
<cmath>
+
    dot(C[i],linewidth(5));
−
\[
+
}
−
P \left( 0 , 3 \right) = \frac{1}{3} , \hspace{1cm}
+
</asy>
−
P \left( 1 , 3 \right) = \frac{7}{36}
+
Note that:
−
\]
 
−
</cmath>
 
−
and
 
−
<cmath>
 
−
\[
 
−
P \left( 1 , 4 \right) = \frac{13}{108}
 
−
\]
 
−
</cmath>
 
−
and
 
−
<cmath>
 
−
\[
 
−
P \left( 0 , 5 \right) = \frac{13}{108} .
 
−
\]
 
−
</cmath>
 
  
−
Therefore, the answer is <math>\boxed{\textbf{(A) }\frac{13}{108}}</math>.
+
* If the bug is at <math>A,</math> then the probability that it moves to <math>B</math> next is <math>1.</math>
  
−
~Steven Chen (www.professorchenedu.com)
+
* If the bug is at <math>B,</math> then the probability that it moves to <math>A</math> next is <math>\frac16.</math>
  
 +
* If the bug is at <math>B,</math> then the probability that it moves to <math>B</math> next is <math>\frac13.</math>
  
−
==Solution 3 (Generating function)==
+
We apply casework to the possible paths of the bug:
−
Use generating function, define <math>c_{n}\cdot x^{n}</math> be <math>c_{n}</math> ways for the end point be <math>{n}</math> unit away from the origins.  
+
<ol style="margin-left: 1.5em;">
 +
  <li><math>A \rightarrow B \rightarrow A \rightarrow B \rightarrow A \rightarrow B</math> <p>
 +
The probability for this case is <math>1\cdot\frac16\cdot1\cdot\frac16\cdot1=\frac{1}{36}.</math></li><p>
 +
  <li><math>A \rightarrow B \rightarrow A \rightarrow B \rightarrow B \rightarrow A</math> <p>
 +
The probability for this case is <math>1\cdot\frac16\cdot1\cdot\frac13\cdot\frac16=\frac{1}{108}.</math></li><p>
 +
  <li><math>A \rightarrow B \rightarrow B \rightarrow A \rightarrow B \rightarrow A</math> <p>
 +
The probability for this case is <math>1\cdot\frac13\cdot\frac16\cdot1\cdot\frac16=\frac{1}{108}.</math></li><p>
 +
  <li><math>A \rightarrow B \rightarrow A \rightarrow B \rightarrow B \rightarrow B</math> <p>
 +
The probability for this case is <math>1\cdot\frac16\cdot1\cdot\frac13\cdot\frac13=\frac{1}{54}.</math></li><p>
 +
  <li><math>A \rightarrow B \rightarrow B \rightarrow A \rightarrow B \rightarrow B</math> <p>
 +
The probability for this case is <math>1\cdot\frac13\cdot\frac16\cdot1\cdot\frac13=\frac{1}{54}.</math></li><p>
 +
  <li><math>A \rightarrow B \rightarrow B \rightarrow B \rightarrow A \rightarrow B</math> <p>
 +
The probability for this case is <math>1\cdot\frac13\cdot\frac13\cdot\frac16\cdot1=\frac{1}{54}.</math></li><p>
 +
  <li><math>A \rightarrow B \rightarrow B \rightarrow B \rightarrow B \rightarrow A</math> <p>
 +
The probability for this case is <math>1\cdot\frac13\cdot\frac13\cdot\frac13\cdot\frac16=\frac{1}{162}.</math></li><p>
 +
  <li><math>A \rightarrow B \rightarrow B \rightarrow B \rightarrow B \rightarrow B</math> <p>
 +
The probability for this case is <math>1\cdot\frac13\cdot\frac13\cdot\frac13\cdot\frac13=\frac{1}{81}.</math></li><p>
 +
</ol>
 +
Together, the answer is <cmath>\frac{1}{36}+\frac{1}{108}+\frac{1}{108}+\frac{1}{54}+\frac{1}{54}+\frac{1}{54}+\frac{1}{162}+\frac{1}{81}=\boxed{\textbf{(A)}\ \frac{13}{108}}.</cmath>
 +
~MRENTHUSIASM
  
−
Therefore,
+
==Solution 6 (Markov Chain)==
 +
We can use a Markov chain to represent the different states of the bug.
 +
[[File:MarkovChain-AMC12B-2021F-17.png|200px|thumb|left|]]
 +
Let "center" (C) represent the starting point, "1 away" (O) represent a point on the grid 1 move and 1 unit away from the starting point, and "2+ away" (T) represent the case where the bug has ventured more than 1 unit away from its starting point.
  
−
if the current point is origin, need to <math>\cdot6{x}</math>
+
Notice that the bug must move to the 1 away state from the center. From there, it moves back to the center with a <math>\frac{1}{6}</math> probability, to a point 2 units away from the center with <math>\frac{1}{2}</math> probability, and to another point 1 unit away with <math>\frac{1}{3}</math> probability.
  
−
if the current point on vertex of the unit hexagon, need to <math>\cdot(x^{-1}+2)</math>, where there is one way to return to the origin and there are two ways to keep distance = 1
+
We are trying to find the probability that the bug does not reach the 2+ away state in 5 moves. To accomplish this, we can find the complement by listing out the cases that the bug does reach the 2+ away state in a specified number of moves.
  
−
Now let's start with <math>p(x)=1</math>; 
+
Clearly, the bug cannot reach the 2+ away (T) state in 0 moves.
  
−
1st step:  <math>p(x)=6x</math> 
+
In 1 move, the bug can only reach the 1 away (O) state, so it cannot reach the T state in 1 move either.
  
−
2nd step:  <math>p(x)=6x\cdot(x^{-1}+2) = 6 + 12x </math>
+
In 2 moves, the bug can move to the O state followed by the T state with probability <math>1*\frac{1}{2} = \frac{1}{2}</math>.
  
−
3rd step:  <math>p(x)=6\cdot6x + 12x\cdot(x^{-1}+2) = 12 + 60x</math>
+
In 3 moves, the bug can follow the pattern OOT with probability <math>1*\frac{1}{3}*\frac{1}{2} = \frac{1}{6}</math>.
  
−
4th step:  <math>p(x)=12\cdot6x + 60x\cdot(x^{-1}+2) = 60 + 192x </math>
+
In 4 moves, the bug can follow the paths of OOOT or OCOT, with probabilities <math>\frac{1}{18}</math> and <math>\frac{1}{12}</math> respectively.
  
−
5th step:  <math>p(x)=60\cdot6x + 192x\cdot(x^{-1}+2) = 192 + 744x </math>
+
In 5 moves, the bug can follow the paths of OOOOT, OCOOT, or OOCOT, with probabilities <math>\frac{1}{54}</math>, <math>\frac{1}{36}</math>, and <math>\frac{1}{36}</math>.
  
−
So there are <math>192+744=936</math> ways for the bug never moves more than 1 unit away from orign, and <math>\frac{936}{6^5} = \boxed{\frac{13}{108}}.</math>
+
Adding up these probabilities, we obtain <math>\frac{95}{108}</math>. Finding the complement of this, we subtract from 1 to get the answer of <math>\boxed{\textbf{(A)}\ \frac{13}{108}}</math>.
 +
<math>\newline</math>
 +
~diyarv
  
 +
==See Also==
 +
{{AMC12 box|year=2021 Fall|ab=B|num-a=18|num-b=16}}
  
−
-wwei.yu
+
[[Category:Intermediate Combinatorics Problems]]
 +
{{MAA Notice}}

Latest revision as of 21:44, 2 November 2024

Problem

A bug starts at a vertex of a grid made of equilateral triangles of side length $1$. At each step the bug moves in one of the $6$ possible directions along the grid lines randomly and independently with equal probability. What is the probability that after $5$ moves the bug never will have been more than $1$ unit away from the starting position?

$\textbf{(A)}\ \frac{13}{108} \qquad\textbf{(B)}\ \frac{7}{54} \qquad\textbf{(C)}\ \frac{29}{216} \qquad\textbf{(D)}\ \frac{4}{27} \qquad\textbf{(E)}\ \frac{1}{16}$

Solution 1 (Recursion)

Let $S(n)$ be the number of paths of $n$ moves such that the bug never will have been more than $1$ unit away from the starting position. Clearly, by symmetry, there are two possible states here, the bug being on the center and the bug being on one of the vertices of the unit hexagon around the center. Let $C(n)$ be the number of paths with the aforementioned restriction that end on the center. Let $V(n)$ be the number of paths with the aforementioned restriction that end on a vertex of the surrounding unit hexagon. We have $S(n) = 6C(n-1) + 3V(n-1),$ since from the center, there are $6$ possible points to land to and from a vertex there are $3$ possible points to land to (the two adjacent vertices and the center). We also have $C(n) = V(n-1)$, since to get to the center the bug must have come from a vertex, and $V(n) = 2V(n-1) + 6C(n-1),$ since from a vertex there are two vertices to move to, and from the center there are $6$ vertices to move to. We can construct a recursion table using the base cases $V(1) = 6$ and $C(1) = 0$ and our recursive rules for $C(n)$ and $V(n)$ as follows: \[\begin{array}{c|c|c} n & V(n) & C(n) \\ \hline & & \\ [-2ex] 1 & 6 & 0 \\ 2 & 12 & 6 \\ 3 & 60 & 12 \\ 4 & 192 & 60 \\ \end{array}\] Then, $S(5) = 6C(4) + 3V(4) = 6 \cdot 60 + 3 \cdot 192 = 936,$ and the desired probability is thus $\frac{936}{6^5} = \boxed{\textbf{(A)}\ \frac{13}{108}}.$

~fidgetboss_4000

Solution 2 (Recursion)

Let $p(i)$ be such probability after $i$ moves. $p(1)=1$, $p(2)=\frac{1}{2}$. Then, $p(3)=\frac{1}{3}\cdot \frac{1}{2}+\frac{1}{6}\cdot 1=\frac{1}{3}$. Then, we can prove the recursive formula \[p(x)=\frac{1}{3}p(x-1)+\frac{1}{6}p(x-2).\] Now, we evaluate $p(5)=\boxed{\textbf{(A)}\ \frac{13}{108}}$.

Solution 3 (Recursion)

We use $(n,t)$ to denote the bug's current state. We wish to find $P(0,5)$.

The first argument $n$ denotes the bug's current position. We use $n = 0$ to denote the bug's starting point. We use $n = 1$ to denote any point whose distance to the bug's starting point is $1$.

The second argument $t$ denotes the remaining number of moves the bug has.

For $n = 0$ and $t \geq 1$, we have \[P(0,t) = P(1,t-1).\] For $n = 1$ and $t \geq 1$, we have \[P(1,t) = \frac{1}{6} P(0,t-1) + \frac{1}{3} P(1,t-1).\] For $n \in \left\{ 0 , 1 \right\}$ and $t = 0$, we have \[P(n,0) = 1.\] We solve this recursive equation by using backward induction: \[\begin{array}{ll} P(0,1) = 1, & P(1,1) = \frac{1}{2}, \\ [1ex] P(0,2) = \frac{1}{2}, & P(1,2) = \frac{1}{3}, \\ [1ex] P(0,3) = \frac{1}{3}, & P(1,3) = \frac{7}{36}, \\ [1ex] P(0,4) = \frac{7}{36}, & P(1,4) = \frac{13}{108}. \end{array}\] Therefore, the answer is $P(0,5) = P(1,4) = \boxed{\textbf{(A)}\ \frac{13}{108}}$.

~Steven Chen (www.professorchenedu.com)

Solution 4 (Generating Function)

Use a generating function, define $c_{n}\cdot x^{n}$ be $c_{n}$ ways for the destination be $n$ units away from the origin.

We conclude that:

  • If the current point is origin, then we need to multiply by $6x$.
  • If the current point on vertex of the unit hexagon, then we need to multiply by $x^{-1}+2$, where there is $1$ way to return to the origin and there are two ways to keep distance $1$.

Now let's start with $p(x)=1$.

$1$st step: $p(x)=6x$

$2$nd step: $p(x)=6x\cdot(x^{-1}+2) = 6 + 12x$

$3$rd step: $p(x)=6\cdot6x + 12x\cdot(x^{-1}+2) = 12 + 60x$

$4$th step: $p(x)=12\cdot6x + 60x\cdot(x^{-1}+2) = 60 + 192x$

$5$th step: $p(x)=60\cdot6x + 192x\cdot(x^{-1}+2) = 192 + 744x$

So, there are $192+744=936$ ways for the bug never moves more than $1$ unit away from origin. The answer is $\frac{936}{6^5} = \boxed{\textbf{(A)}\ \frac{13}{108}}$.

~wwei.yu

Solution 5 (Casework)

In the following diagram, let $A$ denote the vertex where the bug starts (shown in red) and $B$ denote one of the $6$ adjacent vertices (shown in green). [asy] /* Made by MRENTHUSIASM */ size(150); pair[] A, B, C; for (int i = 0; i <= 5; ++i) { A[i] = dir(60*i); B[i] = 2 * dir(60*i); C[i] = sqrt(3) * dir(30+60i); } draw(B[2]--B[3]^^C[1]--C[3]^^B[1]--B[4]^^C[0]--C[4]^^B[0]--B[5]^^B[3]--B[4]^^C[2]--C[4]^^B[2]--B[5]^^C[1]--C[5]^^B[1]--B[0]^^B[2]--B[1]^^C[2]--C[0]^^B[3]--B[0]^^C[3]--C[5]^^B[4]--B[5]); dot(origin,red+linewidth(5)); for (int i = 0; i <= 5; ++i) { dot(A[i],green+linewidth(5)); dot(B[i],linewidth(5)); dot(C[i],linewidth(5)); } [/asy] Note that:

  • If the bug is at $A,$ then the probability that it moves to $B$ next is $1.$
  • If the bug is at $B,$ then the probability that it moves to $A$ next is $\frac16.$
  • If the bug is at $B,$ then the probability that it moves to $B$ next is $\frac13.$

We apply casework to the possible paths of the bug:

  1. $A \rightarrow B \rightarrow A \rightarrow B \rightarrow A \rightarrow B$

    The probability for this case is $1\cdot\frac16\cdot1\cdot\frac16\cdot1=\frac{1}{36}.$

  2. $A \rightarrow B \rightarrow A \rightarrow B \rightarrow B \rightarrow A$

    The probability for this case is $1\cdot\frac16\cdot1\cdot\frac13\cdot\frac16=\frac{1}{108}.$

  3. $A \rightarrow B \rightarrow B \rightarrow A \rightarrow B \rightarrow A$

    The probability for this case is $1\cdot\frac13\cdot\frac16\cdot1\cdot\frac16=\frac{1}{108}.$

  4. $A \rightarrow B \rightarrow A \rightarrow B \rightarrow B \rightarrow B$

    The probability for this case is $1\cdot\frac16\cdot1\cdot\frac13\cdot\frac13=\frac{1}{54}.$

  5. $A \rightarrow B \rightarrow B \rightarrow A \rightarrow B \rightarrow B$

    The probability for this case is $1\cdot\frac13\cdot\frac16\cdot1\cdot\frac13=\frac{1}{54}.$

  6. $A \rightarrow B \rightarrow B \rightarrow B \rightarrow A \rightarrow B$

    The probability for this case is $1\cdot\frac13\cdot\frac13\cdot\frac16\cdot1=\frac{1}{54}.$

  7. $A \rightarrow B \rightarrow B \rightarrow B \rightarrow B \rightarrow A$

    The probability for this case is $1\cdot\frac13\cdot\frac13\cdot\frac13\cdot\frac16=\frac{1}{162}.$

  8. $A \rightarrow B \rightarrow B \rightarrow B \rightarrow B \rightarrow B$

    The probability for this case is $1\cdot\frac13\cdot\frac13\cdot\frac13\cdot\frac13=\frac{1}{81}.$

Together, the answer is \[\frac{1}{36}+\frac{1}{108}+\frac{1}{108}+\frac{1}{54}+\frac{1}{54}+\frac{1}{54}+\frac{1}{162}+\frac{1}{81}=\boxed{\textbf{(A)}\ \frac{13}{108}}.\] ~MRENTHUSIASM

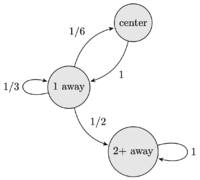
Solution 6 (Markov Chain)

We can use a Markov chain to represent the different states of the bug.

MarkovChain-AMC12B-2021F-17.png

Let "center" (C) represent the starting point, "1 away" (O) represent a point on the grid 1 move and 1 unit away from the starting point, and "2+ away" (T) represent the case where the bug has ventured more than 1 unit away from its starting point.

Notice that the bug must move to the 1 away state from the center. From there, it moves back to the center with a $\frac{1}{6}$ probability, to a point 2 units away from the center with $\frac{1}{2}$ probability, and to another point 1 unit away with $\frac{1}{3}$ probability.

We are trying to find the probability that the bug does not reach the 2+ away state in 5 moves. To accomplish this, we can find the complement by listing out the cases that the bug does reach the 2+ away state in a specified number of moves.

Clearly, the bug cannot reach the 2+ away (T) state in 0 moves.

In 1 move, the bug can only reach the 1 away (O) state, so it cannot reach the T state in 1 move either.

In 2 moves, the bug can move to the O state followed by the T state with probability $1*\frac{1}{2} = \frac{1}{2}$.

In 3 moves, the bug can follow the pattern OOT with probability $1*\frac{1}{3}*\frac{1}{2} = \frac{1}{6}$.

In 4 moves, the bug can follow the paths of OOOT or OCOT, with probabilities $\frac{1}{18}$ and $\frac{1}{12}$ respectively.

In 5 moves, the bug can follow the paths of OOOOT, OCOOT, or OOCOT, with probabilities $\frac{1}{54}$, $\frac{1}{36}$, and $\frac{1}{36}$.

Adding up these probabilities, we obtain $\frac{95}{108}$. Finding the complement of this, we subtract from 1 to get the answer of $\boxed{\textbf{(A)}\ \frac{13}{108}}$. $\newline$ ~diyarv

See Also

2021 Fall AMC 12B (Problems • Answer Key • Resources)
Preceded by
Problem 16 		Followed by
Problem 18
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_Fall_AMC_12B_Problems/Problem_17&oldid=231292"