Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2022 AIME II Problems/Problem 3"

m (Blanked the page)
(Tag: Blanking)
 
(24 intermediate revisions by 11 users not shown)
Line 1: Line 1:
 +
==Problem==
  
 +
A right square pyramid with volume <math>54</math> has a base with side length <math>6.</math> The five vertices of the pyramid all lie on a sphere with radius <math>\frac mn</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>.
 +
 +
==Diagram==
 +
 +
<asy>
 +
import three;
 +
import settings;
 +
leftbutton=new string[] {"rotate","zoom","shift","pan"};
 +
middlebutton=new string[] {""};
 +
rightbutton=new string[] {"zoom","rotateX","rotateY","rotateZ"};
 +
wheelup=new string[] {"zoomin"};
 +
wheeldown=new string[] {"zoomout"};
 +
import three;
 +
pen p = rgb("00FF80")+opacity(0.25);
 +
pen q = rgb("FF8000")+opacity(0.75);
 +
triple A = (-3,-3,0);
 +
triple B = (-3,3,0);
 +
triple C = (3,3,0);
 +
triple D = (3,-3,0);
 +
triple F = (0,0,9/2);
 +
surface sphere = shift((0,0,1/4))*scale3(17/4)*unitsphere;
 +
draw(sphere,p);
 +
draw(A--B--C--D--A--F--B--F--C--F--D--F--A,q);
 +
dot(A);
 +
dot(B);
 +
dot(C);
 +
dot(D);
 +
dot(F);
 +
</asy>
 +
 +
==Solution 1==
 +
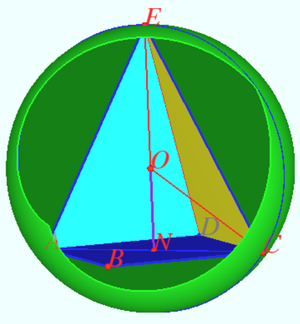
[[File:2022 AIME II 3.png|300px|right]]
 +
Although I can't draw the exact picture of this problem, but it is quite easy to imagine that four vertices of the base of this pyramid is on a circle (Radius <math>\frac{6}{\sqrt{2}} = 3\sqrt{2}</math>). Since all five vertices are on the sphere, the distances of the spherical center and the vertices are the same: <math>l</math>. Because of the symmetrical property of the pyramid,
 +
we can imagine that the line of the apex and the (sphere's) center will intersect the square at the (base's) center.
 +
 +
Since the volume is <math>54 = \frac{1}{3} \cdot S \cdot h = \frac{1}{3} \cdot 6^2 \cdot h</math>, where <math>h=\frac{9}{2}</math> is the height of this pyramid, we have: <math>l^2=\left(\frac{9}{2}-l\right)^2+\left(3\sqrt{2}\right)^2</math> according to the Pythagorean theorem.
 +
 +
Solve this equation will give us <math>l = \frac{17}{4},</math> therefore <math>m+n=\boxed{021}.</math>
 +
 +
==Solution 2==
 +
To start, we find the height of the pyramid. By the volume of a pyramid formula, we have <cmath>\frac13 \cdot 6^2 \cdot h=54 \implies h=\frac92.</cmath> Next, let us find the length of the non-base sides of the pyramid. By the Pythagorean Theorem, noting that the distance from one vertex of the base to the center of the base is <math>\frac12 \cdot 6\sqrt2=3\sqrt2</math>, we have <cmath>x=\sqrt{\left(\frac92\right)^2+(3\sqrt2)^2}=\sqrt{\frac{153}4}=\frac{3\sqrt{17}}2.</cmath> Taking the cross section of the pyramid and transforming the problem into <math>2</math>-d, it suffices to find the radius of the circumcircle of a triangle of side lengths <math>\frac{3\sqrt{17}}2</math>, <math>\frac{3\sqrt{17}}2</math>, <math>6\sqrt2</math>. This turns out to be easy by the formula <math>R=\frac{abc}{4A}</math>, and through computing this value (the work has been left out) we find that <math>R=\frac{17}4</math>, so our answer is <math>\boxed{\textbf{021}}</math>.
 +
 +
~A1001
 +
 +
==Solution 3 (Coord bash)==
 +
By the volume of a pyramid formula, we have that the height of the pyramid is <math>\frac{9}{2}</math>. Since the base is a square with side length 6, the simplest way to place it in the coordinate plane is to put the center of the square at the origin and let the base be on the <math>xy</math> plane. Then, the vertices of the base would be <math>(3,3,0), (3,-3,0), (-3,3,0), (-3,-3,0)</math> in some order. Also, let the vertex be  <math>(0,0,\frac{9}{2})</math>. Recall that the formula for a sphere is <math>(x-a)^2+(y-b)^2+(z-c)^2=r^2</math> where the center is <math>(a,b,c)</math> and the radius is <math>r</math>. Symmetry gives that <math>a=b=0</math>. Plug in <math>(3,3,0)</math> and <math>(0,0,\frac{9}{2})</math> and you get the system of equation
 +
 +
<math>18+c^2=r^2</math>
 +
 +
<math>(\frac{9}{2}-c)^2=r^2</math>
 +
 +
Solving gives <math>c=1/4</math> and <math>r=17/4</math>, so our answer is <math>17+4=\boxed{021}</math>.~[[Ddk001]]
 +
 +
==Video Solution (Mathematical Dexterity)==
 +
https://www.youtube.com/watch?v=UJAYW6YNFVU
 +
 +
==Video Solution by Power of Logic==
 +
https://youtu.be/YieIiYCDytM
 +
 +
==See Also==
 +
{{AIME box|year=2022|n=II|num-b=2|num-a=4}}
 +
{{MAA Notice}}

Latest revision as of 23:33, 28 January 2024

Problem

A right square pyramid with volume $54$ has a base with side length $6.$ The five vertices of the pyramid all lie on a sphere with radius $\frac mn$, where $m$ and $n$ are relatively prime positive integers. Find $m+n$.

Diagram

[asy] import three; import settings; leftbutton=new string[] {"rotate","zoom","shift","pan"}; middlebutton=new string[] {""}; rightbutton=new string[] {"zoom","rotateX","rotateY","rotateZ"}; wheelup=new string[] {"zoomin"}; wheeldown=new string[] {"zoomout"}; import three; pen p = rgb("00FF80")+opacity(0.25); pen q = rgb("FF8000")+opacity(0.75); triple A = (-3,-3,0); triple B = (-3,3,0); triple C = (3,3,0); triple D = (3,-3,0); triple F = (0,0,9/2); surface sphere = shift((0,0,1/4))*scale3(17/4)*unitsphere; draw(sphere,p); draw(A--B--C--D--A--F--B--F--C--F--D--F--A,q); dot(A); dot(B); dot(C); dot(D); dot(F); [/asy]

Solution 1

2022 AIME II 3.png

Although I can't draw the exact picture of this problem, but it is quite easy to imagine that four vertices of the base of this pyramid is on a circle (Radius $\frac{6}{\sqrt{2}} = 3\sqrt{2}$). Since all five vertices are on the sphere, the distances of the spherical center and the vertices are the same: $l$. Because of the symmetrical property of the pyramid, we can imagine that the line of the apex and the (sphere's) center will intersect the square at the (base's) center.

Since the volume is $54 = \frac{1}{3} \cdot S \cdot h = \frac{1}{3} \cdot 6^2 \cdot h$, where $h=\frac{9}{2}$ is the height of this pyramid, we have: $l^2=\left(\frac{9}{2}-l\right)^2+\left(3\sqrt{2}\right)^2$ according to the Pythagorean theorem.

Solve this equation will give us $l = \frac{17}{4},$ therefore $m+n=\boxed{021}.$

Solution 2

To start, we find the height of the pyramid. By the volume of a pyramid formula, we have \[\frac13 \cdot 6^2 \cdot h=54 \implies h=\frac92.\] Next, let us find the length of the non-base sides of the pyramid. By the Pythagorean Theorem, noting that the distance from one vertex of the base to the center of the base is $\frac12 \cdot 6\sqrt2=3\sqrt2$, we have \[x=\sqrt{\left(\frac92\right)^2+(3\sqrt2)^2}=\sqrt{\frac{153}4}=\frac{3\sqrt{17}}2.\] Taking the cross section of the pyramid and transforming the problem into $2$-d, it suffices to find the radius of the circumcircle of a triangle of side lengths $\frac{3\sqrt{17}}2$, $\frac{3\sqrt{17}}2$, $6\sqrt2$. This turns out to be easy by the formula $R=\frac{abc}{4A}$, and through computing this value (the work has been left out) we find that $R=\frac{17}4$, so our answer is $\boxed{\textbf{021}}$.

~A1001

Solution 3 (Coord bash)

By the volume of a pyramid formula, we have that the height of the pyramid is $\frac{9}{2}$. Since the base is a square with side length 6, the simplest way to place it in the coordinate plane is to put the center of the square at the origin and let the base be on the $xy$ plane. Then, the vertices of the base would be $(3,3,0), (3,-3,0), (-3,3,0), (-3,-3,0)$ in some order. Also, let the vertex be $(0,0,\frac{9}{2})$. Recall that the formula for a sphere is $(x-a)^2+(y-b)^2+(z-c)^2=r^2$ where the center is $(a,b,c)$ and the radius is $r$. Symmetry gives that $a=b=0$. Plug in $(3,3,0)$ and $(0,0,\frac{9}{2})$ and you get the system of equation

$18+c^2=r^2$

$(\frac{9}{2}-c)^2=r^2$

Solving gives $c=1/4$ and $r=17/4$, so our answer is $17+4=\boxed{021}$.~Ddk001

Video Solution (Mathematical Dexterity)

https://www.youtube.com/watch?v=UJAYW6YNFVU

Video Solution by Power of Logic

https://youtu.be/YieIiYCDytM

See Also

2022 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 2 		Followed by
Problem 4
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2022_AIME_II_Problems/Problem_3&oldid=213709"