Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2005 AMC 10A Problems/Problem 17"

m (→‎Solution 1)
 
(7 intermediate revisions by 3 users not shown)
Line 20: Line 20:
 
Since <math>d</math> is an integer (difference of sums of integers), and since exactly 2 of the sums must be odd, <math>d</math> must be odd. Therefore, <math>d=1</math>.
 
Since <math>d</math> is an integer (difference of sums of integers), and since exactly 2 of the sums must be odd, <math>d</math> must be odd. Therefore, <math>d=1</math>.
  
−
The middle term must have the majority parity, so it must be odd.  
+
The middle term must have the majority parity, so it must be even.  
 
The 2 terms adjacent to the middle are odd, <math>6+a</math> and <math>6+b</math>. <math>a-b = 2d = 2</math>. <math>a</math> and <math>b</math> can't be the smallest (or largest) 2 odd numbers, because that would make it impossible to construct the smallest (or largest) sum from one of the remaining two numbers and one of the odd numbers. Therefore, <math>\{a,b\} = \{5,7\}</math>. The middle sum must then be <math>(6+5) + 1 = (6+7)-1 = \boxed{12}</math>. The remaining edges are <math>\{9,3\}</math> (because <math>\{5,7\}</math> can't be an edge, as that would make a triangle with 6), <math>\{3,7\}</math>, and <math>\{5,9\}</math>.
 
The 2 terms adjacent to the middle are odd, <math>6+a</math> and <math>6+b</math>. <math>a-b = 2d = 2</math>. <math>a</math> and <math>b</math> can't be the smallest (or largest) 2 odd numbers, because that would make it impossible to construct the smallest (or largest) sum from one of the remaining two numbers and one of the odd numbers. Therefore, <math>\{a,b\} = \{5,7\}</math>. The middle sum must then be <math>(6+5) + 1 = (6+7)-1 = \boxed{12}</math>. The remaining edges are <math>\{9,3\}</math> (because <math>\{5,7\}</math> can't be an edge, as that would make a triangle with 6), <math>\{3,7\}</math>, and <math>\{5,9\}</math>.
  
 
~oinava
 
~oinava
 +
 +
==Solution 3 ==
 +
We notice that the average of <math>3,5,6,7</math> and <math>9</math> is <math>6</math>. Now all we have to do is plug <math>6</math> into each value. This results in all the terms being <math>12</math> and since the term we are looking for is the middle term, we know that our answer is <math>12</math>, <math>\boxed{D}</math>.
  
 
== Video Solution by OmegaLearn ==
 
== Video Solution by OmegaLearn ==
Line 31: Line 34:
  
 
==See Also==
 
==See Also==
−
 
+
[[Category:Introductory Algebra Problems]]
 
{{AMC10 box|year=2005|ab=A|num-b=16|num-a=18}}
 
{{AMC10 box|year=2005|ab=A|num-b=16|num-a=18}}
  
−
[[Category:Introductory Geometry Problems]]
 
−
[[Category:Area Ratio Problems]]
 
 
{{MAA Notice}}
 
{{MAA Notice}}

Latest revision as of 13:25, 13 October 2024

Problem

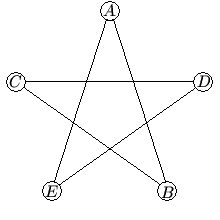
In the five-sided star shown, the letters $A, B, C, D,$ and $E$ are replaced by the numbers $3, 5, 6, 7,$ and $9$, although not necessarily in this order. The sums of the numbers at the ends of the line segments $AB$, $BC$, $CD$, $DE$, and $EA$ form an arithmetic sequence, although not necessarily in that order. What is the middle term of the arithmetic sequence?

2005amc10a17.gif

$\textbf{(A) } 9\qquad \textbf{(B) } 10\qquad \textbf{(C) } 11\qquad \textbf{(D) } 12\qquad \textbf{(E) } 13$

Solution 1

(meta-solving; answer choices imply solution exists)

Each corner $(A,B,C,D,E)$ goes to two sides/numbers. ($A$ goes to $AE$ and $AB$, $D$ goes to $DC$ and $DE$). The sum of every term is equal to $2(3+5+6+7+9)=60$

Since the middle term in an arithmetic sequence is the average of all the terms in the sequence, the middle number is $\frac{60}{5}=\boxed{\textbf{(D) }12}$

Solution 2 (Doesn't assume a solution exists)

We know that the smallest number in the arithmetic sequence must be $\geq 3 + 5 = 8$, and the largest number must be $\leq 7 + 9 = 16$.

Since there are $5$ terms in this sequence, the common difference $d \leq (16 - 8)/(5-1) = 2$.

Since $d$ is an integer (difference of sums of integers), and since exactly 2 of the sums must be odd, $d$ must be odd. Therefore, $d=1$.

The middle term must have the majority parity, so it must be even. The 2 terms adjacent to the middle are odd, $6+a$ and $6+b$. $a-b = 2d = 2$. $a$ and $b$ can't be the smallest (or largest) 2 odd numbers, because that would make it impossible to construct the smallest (or largest) sum from one of the remaining two numbers and one of the odd numbers. Therefore, $\{a,b\} = \{5,7\}$. The middle sum must then be $(6+5) + 1 = (6+7)-1 = \boxed{12}$. The remaining edges are $\{9,3\}$ (because $\{5,7\}$ can't be an edge, as that would make a triangle with 6), $\{3,7\}$, and $\{5,9\}$.

~oinava

Solution 3

We notice that the average of $3,5,6,7$ and $9$ is $6$. Now all we have to do is plug $6$ into each value. This results in all the terms being $12$ and since the term we are looking for is the middle term, we know that our answer is $12$, $\boxed{D}$.

Video Solution by OmegaLearn

https://youtu.be/tKsYSBdeVuw?t=544

~ pi_is_3.14

See Also

2005 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 16 		Followed by
Problem 18
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2005_AMC_10A_Problems/Problem_17&oldid=229731"