Difference between revisions of "2005 AIME I Problems/Problem 1"
(→Problem) |
m (→Solution) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 5: | Line 5: | ||
== Solution == | == Solution == | ||
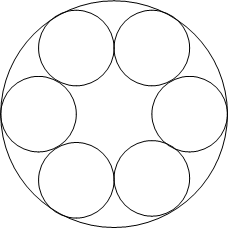
| − | Define the radii of the six congruent circles as <math>r</math>. If we draw all of the radii to the points of external tangency, we get a [[regular polygon|regular]] [[hexagon]]. If we connect the [[vertex|vertices]] of the hexagon to the [[center]] of the circle <math>C</math>, we form several [[equilateral triangle]]s. The length of each side of the triangle is <math>2r</math>. Notice that the radius of circle <math>C</math> is equal to the length of the side of the triangle plus <math>r</math>. Thus, the radius of <math>C</math> has a length of <math>3r = 30</math>, and so <math>r = 10</math>. <math>K = 30^2\pi - 6(10^2\pi) = 300\pi</math>, so <math>\lfloor 300\pi \rfloor = 942</math>. | + | Define the radii of the six congruent circles as <math>r</math>. If we draw all of the radii to the points of external tangency, we get a [[regular polygon|regular]] [[hexagon]]. If we connect the [[vertex|vertices]] of the hexagon to the [[center]] of the circle <math>C</math>, we form several [[equilateral triangle]]s. The length of each side of the triangle is <math>2r</math>. Notice that the radius of circle <math>C</math> is equal to the length of the side of the triangle plus <math>r</math>. Thus, the radius of <math>C</math> has a length of <math>3r = 30</math>, and so <math>r = 10</math>. <math>K = 30^2\pi - 6(10^2\pi) = 300\pi</math>, so <math>\lfloor 300\pi \rfloor = \boxed{942}</math>. |
== See also == | == See also == | ||
| Line 11: | Line 11: | ||
[[Category:Intermediate Geometry Problems]] | [[Category:Intermediate Geometry Problems]] | ||
| + | {{MAA Notice}} | ||
Latest revision as of 12:17, 22 July 2017
Problem
Six congruent circles form a ring with each circle externally tangent to two circles adjacent to it. All circles are internally tangent to a circle 
with radius 30. Let 
be the area of the region inside circle and outside of the six circles in the ring. Find 
(the floor function).
Solution
Define the radii of the six congruent circles as 
. If we draw all of the radii to the points of external tangency, we get a regular hexagon. If we connect the vertices of the hexagon to the center of the circle , we form several equilateral triangles. The length of each side of the triangle is 
. Notice that the radius of circle is equal to the length of the side of the triangle plus . Thus, the radius of has a length of 
, and so 
. 
, so 
.
See also
| 2005 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by First Question |
Followed by Problem 2 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
