Difference between revisions of "2012 AIME I Problems/Problem 12"
(→Solution 2) |
Boxtheanswer (talk | contribs) m (→Solution 9) |
||
| (36 intermediate revisions by 16 users not shown) | |||
| Line 1: | Line 1: | ||
| − | ==Problem | + | ==Problem== |
Let <math>\triangle ABC</math> be a right triangle with right angle at <math>C.</math> Let <math>D</math> and <math>E</math> be points on <math>\overline{AB}</math> with <math>D</math> between <math>A</math> and <math>E</math> such that <math>\overline{CD}</math> and <math>\overline{CE}</math> trisect <math>\angle C.</math> If <math>\frac{DE}{BE} = \frac{8}{15},</math> then <math>\tan B</math> can be written as <math>\frac{m \sqrt{p}}{n},</math> where <math>m</math> and <math>n</math> are relatively prime positive integers, and <math>p</math> is a positive integer not divisible by the square of any prime. Find <math>m+n+p.</math> | Let <math>\triangle ABC</math> be a right triangle with right angle at <math>C.</math> Let <math>D</math> and <math>E</math> be points on <math>\overline{AB}</math> with <math>D</math> between <math>A</math> and <math>E</math> such that <math>\overline{CD}</math> and <math>\overline{CE}</math> trisect <math>\angle C.</math> If <math>\frac{DE}{BE} = \frac{8}{15},</math> then <math>\tan B</math> can be written as <math>\frac{m \sqrt{p}}{n},</math> where <math>m</math> and <math>n</math> are relatively prime positive integers, and <math>p</math> is a positive integer not divisible by the square of any prime. Find <math>m+n+p.</math> | ||
| − | == Solution == | + | |
| − | === Solution | + | == Solution 1 == |
| + | We have <math>\angle BCE = \angle ECD = \angle DCA = \tfrac 13 \cdot 90^\circ = 30^\circ</math>. Drop the altitude from <math>D</math> to <math>CB</math> and call the foot <math>F</math>. | ||
| + | <center><asy>import cse5;size(200); | ||
| + | defaultpen(linewidth(0.4)+fontsize(8)); | ||
| + | |||
| + | pair A,B,C,D,E0,F; | ||
| + | C=origin; | ||
| + | B=(10,0); | ||
| + | A=(0,5); | ||
| + | E0=extension(C,dir(30),A,B); | ||
| + | D=extension(C,dir(60),A,B); | ||
| + | F=foot(D,C,B); | ||
| + | |||
| + | draw(A--B--C--A, black+0.8); | ||
| + | draw(C--D--F^^C--E0, gray); | ||
| + | dot("$A$",A,N); | ||
| + | dot("$B$",B,SE); | ||
| + | dot("$C$",C,SW); | ||
| + | dot("$D$",D,NE); | ||
| + | dot("$E$",E0,2*NE); | ||
| + | dot("$F$",F,S); | ||
| + | |||
| + | label("$8$",D--E0,2*NE); | ||
| + | label("$15$",E0--B,2*NE); | ||
| + | label("$11a$",C--B,2*S); | ||
| + | label(rotate(60)*"$8a$",C--D,2*NW); | ||
| + | label(rotate(-90)*"$4\sqrt{3}a$",D--F, E); | ||
| + | label("$4a$",C--F,2*S); | ||
| + | </asy></center> | ||
| + | Let <math>CD = 8a</math>. Using angle bisector theorem on <math>\triangle CDB</math>, we get <math>CB = 15a</math>. Now <math>CDF</math> is a <math>30</math>-<math>60</math>-<math>90</math> triangle, so <math>CF = 4a</math>, <math>FD = 4a\sqrt{3}</math>, and <math>FB = 11a</math>. Finally, <math>\tan{B} = \tfrac{DF}{FB}=\tfrac{4\sqrt{3}a}{11a} = \tfrac{4\sqrt{3}}{11}</math>. Our final answer is <math>4 + 3 + 11 = \boxed{018}</math>. | ||
| + | |||
| + | == Solution 2 == | ||
Without loss of generality, set <math>CB = 1</math>. Then, by the Angle Bisector Theorem on triangle <math>DCB</math>, we have <math>CD = \frac{8}{15}</math>. We apply the Law of Cosines to triangle <math>DCB</math> to get <math>1 + \frac{64}{225} - \frac{8}{15} = BD^{2}</math>, which we can simplify to get <math>BD = \frac{13}{15}</math>. | Without loss of generality, set <math>CB = 1</math>. Then, by the Angle Bisector Theorem on triangle <math>DCB</math>, we have <math>CD = \frac{8}{15}</math>. We apply the Law of Cosines to triangle <math>DCB</math> to get <math>1 + \frac{64}{225} - \frac{8}{15} = BD^{2}</math>, which we can simplify to get <math>BD = \frac{13}{15}</math>. | ||
| Line 10: | Line 41: | ||
Our final answer is <math>4+3+11 = \boxed{018}</math>. | Our final answer is <math>4+3+11 = \boxed{018}</math>. | ||
| − | + | == Solution 3 == | |
| − | |||
(This solution does not use the Angle Bisector Theorem or the Law of Cosines, but it uses the Law of Sines and more trig) | (This solution does not use the Angle Bisector Theorem or the Law of Cosines, but it uses the Law of Sines and more trig) | ||
| Line 28: | Line 58: | ||
Use a trig identity on the denominator on the right to obtain: <math>\frac{8}{15} = \frac{\sin B}{\sin 120 \cos B - \cos 120 \sin B}</math> | Use a trig identity on the denominator on the right to obtain: <math>\frac{8}{15} = \frac{\sin B}{\sin 120 \cos B - \cos 120 \sin B}</math> | ||
| − | This simplifies to <math>\frac{8}{15} = \frac{\sin B}{\frac{\sqrt{3}\cos B}{2} + \frac{\sin B}{2}} = \frac{\sin B}{\frac{\sqrt{3} \ | + | This simplifies to <math>\frac{8}{15} = \frac{\sin B}{\frac{\sqrt{3}\cos B}{2} + \frac{\sin B}{2}} = \frac{\sin B}{\frac{\sqrt{3} \cos B + \sin B}{2}} = \frac{2\sin B}{\sqrt{3}\cos B + \sin B}</math> |
This gives <math>8\sqrt{3}\cos B+8\sin B=30\sin B</math> | This gives <math>8\sqrt{3}\cos B+8\sin B=30\sin B</math> | ||
| − | Dividing by <math> | + | Dividing by <math>\cos B</math>, we have <math>{8\sqrt{3}}= 22\tan B</math> |
| − | < | + | <math>\tan{B} = \frac{8\sqrt{3}}{22} = \frac{4\sqrt{3}}{11}</math>. Our final answer is <math>4 + 3 + 11 = \boxed{018}</math>. |
| − | + | == Solution 4 == | |
(This solution avoids advanced trigonometry) | (This solution avoids advanced trigonometry) | ||
| Line 47: | Line 77: | ||
Thus <math>\tan \angle B = \frac{x}{\frac{11\sqrt{3}}{12}x}=\frac{4\sqrt{3}}{11}</math>, and our answer is <math>4+3+11=\boxed{018}</math>. | Thus <math>\tan \angle B = \frac{x}{\frac{11\sqrt{3}}{12}x}=\frac{4\sqrt{3}}{11}</math>, and our answer is <math>4+3+11=\boxed{018}</math>. | ||
| + | |||
| + | == Solution 5 == | ||
| + | (Another solution without trigonometry) | ||
| + | |||
| + | Extend <math>CD</math> to point <math>F</math> such that <math>\overline{AF} \parallel \overline{CB}</math>. It is then clear that <math>\triangle AFD</math> is similar to <math>\triangle BCD</math>. | ||
| + | |||
| + | Let <math>AC=p</math>, <math>BC=q</math>. Then <math>\tan \angle B = p/q</math>. | ||
| + | |||
| + | With the Angle Bisector Theorem, we get that <math>CD=\frac{8}{15}q</math>. From 30-60-90 <math>\triangle CAF</math>, we get that <math>AF=\frac{1}{\sqrt{3}}p</math> and <math>FD=FC-CD=\frac{2}{\sqrt{3}}p-\frac{8}{15}q</math>. | ||
| + | |||
| + | From <math>\triangle AFD \sim \triangle BCD</math>, we have that <math>\frac{FD}{CD}=\frac{FA}{CB}=\frac{\frac{2}{\sqrt{3}}p-\frac{8}{15}q}{\frac{8}{15}q}=\frac{\frac{1}{\sqrt{3}}p}{q}</math>. Simplifying yields <math>\left(\frac{p}{q}\right)\left(\frac{2\sqrt{3}}{3}*\frac{15}{8}-\frac{\sqrt{3}}{3}\right)=1</math>, and <math>\tan \angle B=\frac{p}{q}=\frac{4\sqrt{3}}{11}</math>, so our answer is <math>4+3+11=\boxed{018}</math>. | ||
| + | |||
| + | == Solution 6 == | ||
| + | Let <math>CB = 1</math>, and let the feet of the altitudes from <math>D</math> and <math>E</math> to <math>\overline{CB}</math> be <math>D'</math> and <math>E'</math>, respectively. Also, let <math>DE = 8k</math> and <math>EB = 15k</math>. We see that <math>BD' = 15k\cos B</math> and <math>BE' = 23k\cos B</math> by right triangles <math>\triangle{BDD'}</math> and <math>\triangle{BEE'}</math>. From this we have that <math>D'E' = 8k\cos B</math>. With the same triangles we have <math>DD' = 23k\sin B</math> and <math>EE' = 15k\sin B</math>. From 30-60-90 triangles <math>\triangle{CDD'}</math> and <math>\triangle{CEE'}</math>, we see that <math>CD' = \frac{23k\sqrt{3}\sin B}{3}</math> and <math>CE' = 15k\sqrt{3}\sin B</math>, so <math>D'E' = \frac{22k\sqrt{3}\sin B}{3}</math>. From our two values of <math>D'E'</math> we get: | ||
| + | <math>8k\cos B = \frac{22k\sqrt{3}\sin B}{3}</math> | ||
| + | |||
| + | <math>\frac{\sin B}{\cos B} = \frac{8k}{\frac{22k\sqrt{3}}{3}} = \tan B</math> | ||
| + | |||
| + | <math>\tan B = \frac{8}{\frac{22\sqrt{3}}{3}} = \frac{24}{22\sqrt{3}} = \frac{8\sqrt{3}}{22} = \frac{4\sqrt{3}}{11}</math> | ||
| + | Our answer is then <math>4+3+11 = \boxed{018}</math>. | ||
| + | |||
| + | == Video Solution by Richard Rusczyk == | ||
| + | |||
| + | https://artofproblemsolving.com/videos/amc/2012aimei/352 | ||
| + | |||
| + | ==Solution 7== | ||
| + | WLOG, let <math>DE=8</math> and <math>BE=15</math>. First, by the Law of Sines on <math>\triangle CEB</math>, we find that | ||
| + | <cmath>\frac{\sin\angle B}{CE}=\frac{\sin\angle ECB}{BE}=\frac{1}{30}\implies \sin\angle B=\frac{CE}{30}.</cmath> | ||
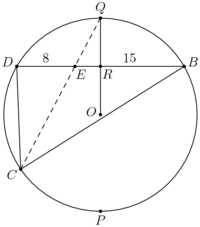
| + | Now, we will find <math>CE</math>. Consider the following diagram: | ||
| + | [[Image:2012 AIME I -12 Sol 7 Diagram.png|200px|thumb|left| ]] | ||
| + | We have constructed equilateral triangle <math>\triangle BDP</math>, and its circumcircle. Since <math>\angle DCB=\angle DPB=60^\circ</math>, <math>C</math> lies on <math>(BDP)</math> as well. Let <math>Q</math> be the point diametrically opposite <math>P</math> on <math>(BCD)</math>, and let <math>R</math> be the foot of <math>Q</math> on <math>BD</math> (this is the midpoint of <math>BD</math>). It is easy to compute that <math>RQ=\frac{23}{2\sqrt3}</math> and <math>ER=\frac{23}{2}-8=\frac{7}{2}</math>. Therefore, by the Pythagorean Theorem, <math>EQ=\frac{13}{\sqrt{3}}</math>. Now, by Power of a Point, we know that <math>(DE)(BE)=(EQ)(EC)</math>, which means that | ||
| + | <cmath>120=\frac{13EC}{\sqrt{3}}\implies EC=\frac{120\sqrt{3}}{13}.</cmath> | ||
| + | From before, we know that <math>\sin\angle B=\frac{EC}{30}\implies \sin\angle B=\frac{4\sqrt3}{13}</math>. It's now easy to compute <math>\cos\angle B</math> as well using the Pythagorean identity; we find that <math>\cos\angle B=\frac{11}{13}</math>, and thus <math>\tan\angle B=\frac{4\sqrt3}{11}</math> for an answer of <math>\boxed{018}</math>. | ||
| + | -brainiacmaniac31 | ||
| + | |||
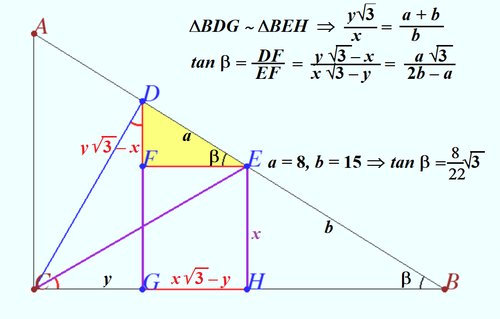
| + | ==Solution 8== | ||
| + | [[File:2012 AIME 12.png|500px]] | ||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
| + | |||
| + | ==Solution 9== | ||
| + | WLOG, let <math>DE=8</math> and <math>EB=15</math>. (this will be redefined later) | ||
| + | Define points <math>A'</math>, <math>D'</math>, <math>E'</math>, and <math>B'</math> such that <math>A'</math> is on <math>AC</math>, <math>B'</math> is on <math>CB</math> and <math>D'</math> and <math>E'</math> are the intersections of <math>A'B'</math> with <math>CD</math> and <math>CE</math>, with <math>CD' = CE' = 1</math>, respectively. From cross ratios, we have: | ||
| + | \begin {align*} | ||
| + | \frac{(AE)(DB)}{(AB)(DE)} &= \frac{(A'E')(D'B')}{(A'B')(D'E')} \\ | ||
| + | \frac{(AD+8)(23)}{(AD+23)(8)} & = \frac{(\cos(15)+\sin(15))^2}{(2 \cos(15))(2 \sin(15))} \\ | ||
| + | & \implies AD = 92/11 | ||
| + | \end {align*} | ||
| + | For simplicity, scale everything by <math>11</math>, so <math>AD=92</math>, <math>DE=88</math> and <math>EB = 165</math>. | ||
| + | From the ratio lemma, we have: | ||
| + | \begin {align*} | ||
| + | \frac{AC}{CB} &= \frac{AD \sin{\angle BCD}}{DB \sin{\angle ACD}} \\ | ||
| + | \tan B &= \frac{92 \cdot \sqrt{3}/2}{253 \cdot 1/2} \\ | ||
| + | \tan B &= \frac{4 \sqrt{3}}{2}\\ | ||
| + | &\implies \boxed{018}. | ||
| + | \end{align*} | ||
| + | ~ boxtheanswer | ||
== See also == | == See also == | ||
{{AIME box|year=2012|n=I|num-b=11|num-a=13}} | {{AIME box|year=2012|n=I|num-b=11|num-a=13}} | ||
{{MAA Notice}} | {{MAA Notice}} | ||
Latest revision as of 00:26, 12 September 2024
Contents
Problem
Let ![]() be a right triangle with right angle at
be a right triangle with right angle at ![]() Let
Let ![]() and
and ![]() be points on
be points on ![]() with
with ![]() between
between ![]() and
and ![]() such that
such that ![]() and
and ![]() trisect
trisect ![]() If
If ![]() then
then ![]() can be written as
can be written as ![]() where
where ![]() and
and ![]() are relatively prime positive integers, and
are relatively prime positive integers, and ![]() is a positive integer not divisible by the square of any prime. Find
is a positive integer not divisible by the square of any prime. Find ![]()
Solution 1
We have ![]() . Drop the altitude from
. Drop the altitude from ![]() to
to ![]() and call the foot
and call the foot ![]() .
.
![[asy]import cse5;size(200); defaultpen(linewidth(0.4)+fontsize(8)); pair A,B,C,D,E0,F; C=origin; B=(10,0); A=(0,5); E0=extension(C,dir(30),A,B); D=extension(C,dir(60),A,B); F=foot(D,C,B); draw(A--B--C--A, black+0.8); draw(C--D--F^^C--E0, gray); dot("$A$",A,N); dot("$B$",B,SE); dot("$C$",C,SW); dot("$D$",D,NE); dot("$E$",E0,2*NE); dot("$F$",F,S); label("$8$",D--E0,2*NE); label("$15$",E0--B,2*NE); label("$11a$",C--B,2*S); label(rotate(60)*"$8a$",C--D,2*NW); label(rotate(-90)*"$4\sqrt{3}a$",D--F, E); label("$4a$",C--F,2*S); [/asy]](http://latex.artofproblemsolving.com/9/d/4/9d434997e7b736adb2b4248a976dc241884d063a.png)
Let ![]() . Using angle bisector theorem on
. Using angle bisector theorem on ![]() , we get
, we get ![]() . Now
. Now ![]() is a
is a ![]() -
-![]() -
-![]() triangle, so
triangle, so ![]() ,
, ![]() , and
, and ![]() . Finally,
. Finally, ![]() . Our final answer is
. Our final answer is ![]() .
.
Solution 2
Without loss of generality, set ![]() . Then, by the Angle Bisector Theorem on triangle
. Then, by the Angle Bisector Theorem on triangle ![]() , we have
, we have ![]() . We apply the Law of Cosines to triangle
. We apply the Law of Cosines to triangle ![]() to get
to get ![]() , which we can simplify to get
, which we can simplify to get ![]() .
.
Now, we have ![]() by another application of the Law of Cosines to triangle
by another application of the Law of Cosines to triangle ![]() , so
, so ![]() . In addition,
. In addition, ![]() , so
, so ![]() .
.
Our final answer is ![]() .
.
Solution 3
(This solution does not use the Angle Bisector Theorem or the Law of Cosines, but it uses the Law of Sines and more trig)
Find values for all angles in terms of ![]() .
. ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
Use the law of sines on ![]() and
and ![]() :
:
In ![]() ,
, ![]() . This simplifies to
. This simplifies to ![]() .
.
In ![]() ,
, ![]() . This simplifies to
. This simplifies to ![]() .
.
Solve for ![]() and equate them so that you get
and equate them so that you get ![]() .
.
From this, ![]() .
.
Use a trig identity on the denominator on the right to obtain: ![]()
This simplifies to ![]()
This gives ![]() Dividing by
Dividing by ![]() , we have
, we have ![]()
![]() . Our final answer is
. Our final answer is ![]() .
.
Solution 4
(This solution avoids advanced trigonometry)
Let ![]() be the foot of the perpendicular from
be the foot of the perpendicular from ![]() to
to ![]() , and let
, and let ![]() be the foot of the perpendicular from
be the foot of the perpendicular from ![]() to
to ![]() .
.
Now let ![]() . Clearly, triangles
. Clearly, triangles ![]() and
and ![]() are similar with
are similar with ![]() , so
, so ![]() .
.
Since triangles ![]() and
and ![]() are 30-60-90 right triangles, we can easily find other lengths in terms of
are 30-60-90 right triangles, we can easily find other lengths in terms of ![]() . For example, we see that
. For example, we see that ![]() and
and ![]() . Therefore
. Therefore ![]() .
.
Again using the fact that triangles ![]() and
and ![]() are similar, we see that
are similar, we see that ![]() , so
, so ![]() .
.
Thus  , and our answer is
, and our answer is ![]() .
.
Solution 5
(Another solution without trigonometry)
Extend ![]() to point
to point ![]() such that
such that ![]() . It is then clear that
. It is then clear that ![]() is similar to
is similar to ![]() .
.
Let ![]() ,
, ![]() . Then
. Then ![]() .
.
With the Angle Bisector Theorem, we get that ![]() . From 30-60-90
. From 30-60-90 ![]() , we get that
, we get that ![]() and
and ![]() .
.
From ![]() , we have that
, we have that ![]() . Simplifying yields
. Simplifying yields  , and
, and ![]() , so our answer is
, so our answer is ![]() .
.
Solution 6
Let ![]() , and let the feet of the altitudes from
, and let the feet of the altitudes from ![]() and
and ![]() to
to ![]() be
be ![]() and
and ![]() , respectively. Also, let
, respectively. Also, let ![]() and
and ![]() . We see that
. We see that ![]() and
and ![]() by right triangles
by right triangles ![]() and
and ![]() . From this we have that
. From this we have that ![]() . With the same triangles we have
. With the same triangles we have ![]() and
and ![]() . From 30-60-90 triangles
. From 30-60-90 triangles ![]() and
and ![]() , we see that
, we see that ![]() and
and ![]() , so
, so ![]() . From our two values of
. From our two values of ![]() we get:
we get:
![]()
![]()
 Our answer is then
Our answer is then ![]() .
.
Video Solution by Richard Rusczyk
https://artofproblemsolving.com/videos/amc/2012aimei/352
Solution 7
WLOG, let ![]() and
and ![]() . First, by the Law of Sines on
. First, by the Law of Sines on ![]() , we find that
, we find that
![]() Now, we will find
Now, we will find ![]() . Consider the following diagram:
. Consider the following diagram:
We have constructed equilateral triangle ![]() , and its circumcircle. Since
, and its circumcircle. Since ![]() ,
, ![]() lies on
lies on ![]() as well. Let
as well. Let ![]() be the point diametrically opposite
be the point diametrically opposite ![]() on
on ![]() , and let
, and let ![]() be the foot of
be the foot of ![]() on
on ![]() (this is the midpoint of
(this is the midpoint of ![]() ). It is easy to compute that
). It is easy to compute that ![]() and
and ![]() . Therefore, by the Pythagorean Theorem,
. Therefore, by the Pythagorean Theorem, ![]() . Now, by Power of a Point, we know that
. Now, by Power of a Point, we know that ![]() , which means that
, which means that
![]() From before, we know that
From before, we know that ![]() . It's now easy to compute
. It's now easy to compute ![]() as well using the Pythagorean identity; we find that
as well using the Pythagorean identity; we find that ![]() , and thus
, and thus ![]() for an answer of
for an answer of ![]() .
-brainiacmaniac31
.
-brainiacmaniac31
Solution 8
 vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Solution 9
WLOG, let ![]() and
and ![]() . (this will be redefined later)
Define points
. (this will be redefined later)
Define points ![]() ,
, ![]() ,
, ![]() , and
, and ![]() such that
such that ![]() is on
is on ![]() ,
, ![]() is on
is on ![]() and
and ![]() and
and ![]() are the intersections of
are the intersections of ![]() with
with ![]() and
and ![]() , with
, with ![]() , respectively. From cross ratios, we have:
\begin {align*}
\frac{(AE)(DB)}{(AB)(DE)} &= \frac{(A'E')(D'B')}{(A'B')(D'E')} \\
\frac{(AD+8)(23)}{(AD+23)(8)} & = \frac{(\cos(15)+\sin(15))^2}{(2 \cos(15))(2 \sin(15))} \\
& \implies AD = 92/11
\end {align*}
For simplicity, scale everything by
, respectively. From cross ratios, we have:
\begin {align*}
\frac{(AE)(DB)}{(AB)(DE)} &= \frac{(A'E')(D'B')}{(A'B')(D'E')} \\
\frac{(AD+8)(23)}{(AD+23)(8)} & = \frac{(\cos(15)+\sin(15))^2}{(2 \cos(15))(2 \sin(15))} \\
& \implies AD = 92/11
\end {align*}
For simplicity, scale everything by ![]() , so
, so ![]() ,
, ![]() and
and ![]() .
From the ratio lemma, we have:
\begin {align*}
\frac{AC}{CB} &= \frac{AD \sin{\angle BCD}}{DB \sin{\angle ACD}} \\
\tan B &= \frac{92 \cdot \sqrt{3}/2}{253 \cdot 1/2} \\
\tan B &= \frac{4 \sqrt{3}}{2}\\
&\implies \boxed{018}.
\end{align*}
~ boxtheanswer
.
From the ratio lemma, we have:
\begin {align*}
\frac{AC}{CB} &= \frac{AD \sin{\angle BCD}}{DB \sin{\angle ACD}} \\
\tan B &= \frac{92 \cdot \sqrt{3}/2}{253 \cdot 1/2} \\
\tan B &= \frac{4 \sqrt{3}}{2}\\
&\implies \boxed{018}.
\end{align*}
~ boxtheanswer
See also
| 2012 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 11 |
Followed by Problem 13 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.